▷ Integrales

En este post te explicamos qué es una integral y para qué sirve en matemáticas. Así pues, encontrarás la definición de integral, las fórmulas para resolver integrales, cuáles son los diferentes tipos de integrales y, además, cuáles son sus propiedades.

Índice

¿Qué son las integrales?

En matemáticas, la integración es la operación opuesta a la derivación, por lo tanto, la integral es la operación opuesta a la derivada. Es decir, las integrales son aquellas operaciones matemáticas mediante las cuales se puede calcular la función primitiva de una derivada.

Así pues, según el teorema fundamental del cálculo, al integrar una función continua y luego calcular su derivada se obtiene la función original.

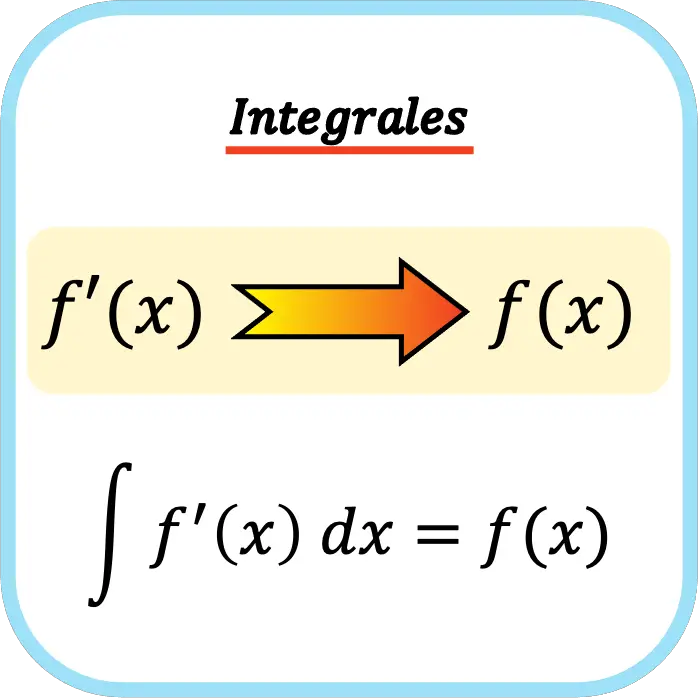
Si una función tiene integral, se dice que esa función es integrable. Asimismo, las integrales tienen su propia terminología:

$\displaystyle\int_a^b f(x)\ dx$

$\displaystyle\int$ es el signo de integración.
$\displaystyle a$ es el límite inferior de la integración.
$\displaystyle b$ es el límite superior de la integración.
$\displaystyle f(x)$ es la función a integrar, también llamada integrando.
$\displaystyle dx$ es el diferencial de x, que indica la variable de la función que se integra.

En algunos casos las integrales no tienen límites de integración, lo que significa que se integra la función para todo su dominio. Más abajo veremos cuáles son los diferentes tipos de integrales.

En definitiva, las integrales son las operaciones matemáticas opuestas a las derivadas. De manera que si derivamos el resultado de una integral, conseguiremos la función original otra vez.

➤ Ver: Derivadas

Fórmulas de integrales

A continuación se muestran las fórmulas de las integrales más utilizadas, no obstante, puede que te resulte más útil ver una tabla con las fórmulas de las integrales. Por eso te dejamos la siguiente tabla en la que se muestran cuáles son todas las fórmulas de las integrales:

➤ Ver: Tabla de integrales

Integral de una constante

La integral de una función constante es igual a la constante multiplicada por x más la constante de integración.

$\displaystyle\int k \ dx=kx+C$

➤ Ver: Ejercicios resueltos de integrales de constantes

Integral de una potencia

La integral de una potencia de x es igual a x elevado a la potencia más uno dividido por la potencia más uno.

$\displaystyle\int x^ndx=\cfrac{x^{n+1}}{n+1}+C$

➤ Ver: Ejercicios resueltos de integrales de potencias

Integral de una función exponencial

La integral de una función exponencial, es decir, de una constante elevada a la x, es igual a la función exponencial partido por el logaritmo neperiano de su base.

$\displaystyle \int a^x dx=\cfrac{a^x}{\ln a}+C$

➤ Ver: Ejercicios resueltos de integrales de funciones exponenciales

Integral de una función logarítmica

Las fórmulas para resolver integrales logarítmicas son las siguientes:

$\displaystyle\int\frac{1}{x}\ dx= \ln|x| + C$

$\displaystyle\int\ln(x)\ dx= x\cdot \ln(x) -x+ C$

$\displaystyle\int\log_a(x)\ dx= \frac{x}{\ln(a)}\cdot \bigl(\ln(x)-1\bigr)+ C$

➤ Ver: Ejercicios resueltos de integrales de funciones logarítmicas

Integrales trigonométricas

Las fórmulas para resolver las integrales de las principales funciones trigonométricas son las siguientes:

$\displaystyle\int\text{sen}(x)\ dx=-\text{cos}(x)+C$

$\displaystyle\int\text{cos}(x)\ dx=\text{sen}(x)+C$

$\displaystyle\int\text{tan}(x)\ dx=-\ln |cos(x)|+C$

Estas fórmulas sirven para resolver la integral del seno, del coseno o de la tangente, no obstante, hay otras funciones trigonométricas cuyas integrales son más difíciles (como la secante, la cosecante o el arcotangente). Para ver todas las fórmulas de las integrales trigonométricas y practicar con ejercicios resueltos haz clic aquí:

➤ Ver: Ejercicios resueltos de integrales de funciones trigonométricas

Tipos de integrales

Los tipos de integrales son:

Integrales indefinidas.
Integrales definidas.

A continuación te explicamos cada tipo de integral detalladamente.

Integrales indefinidas

Una integral indefinida consiste en calcular la función primitiva de una función. Es decir, dada una función f(x), la integral indefinida de la función f(x) es igual al conjunto de funciones que al ser derivadas dan como resultado f(x).

Así pues, la función obtenida de resolver una integral indefinida se llama función primitiva o antiderivada.

$\displaystyle\int f(x)\ dx$

Este tipo de integrales se caracterizan por no tener límites de integración, de manera que se integra la función en todo su dominio.

➤ Ver: Ejercicios resueltos de integrales indefinidas

Integrales definidas

Las integrales definidas son integrales que sirven para calcular el área de la región comprendida entre la función y el eje de abscisas en un intervalo determinado.

Por lo tanto, la integral definida de la función f(x) en el intervalo [a,b] es igual al área entre la gráfica de f(x), el eje X y las rectas verticales x=a y x=b.

Así pues, las integrales definidas se representan de la siguiente manera:

$\displaystyle\int_a^b f(x)\ dx$

La principal diferencia entre las integrales definidas y las integrales indefinidas es que las integrales definidas dan como resultado un valor, mientras que el resultado de las integrales indefinidas son funciones.

➤ Ver: Ejercicios resueltos de integrales definidas

Propiedades de las integrales

Las integrales tienen las siguientes propiedades:

La integral de una suma (o resta) de funciones es igual a la suma (o resta) de la integral de cada función por separado.

$\displaystyle\int\bigl[f(x)\pm (x)\bigr]\ dx=\int f(x)\ dx\pm \int g(x)\ dx$

La integral del producto de una constante por una función es equivalente al producto de la constante por la integral de la función.

$\displaystyle\int k\cdot f(x)\ dx=k\int f(x)\ dx$

Si una función es menor o igual que otra, la integral de la primera función también es menor o igual que la integral de la segunda función.

$\displaystyle f(x)\leq g(x) \ \Rightarrow \ \int f(x) \ dx \leq \int g(x) \ dx$

El valor absoluto de la integral de una función es menor o igual que la integral del valor absoluto de dicha función.

$\displaystyle |f(x)| \text{ integrable} \ \Rightarrow \left|\int f(x)\ dx\right| \leq \int |f(x)| \ dx$

Si se cambian los límites de integración de una integral definida, el resultado es el mismo pero cambiado de signo.

$\displaystyle\int_a^b f(x)\ dx=-\int_b^a f(x)\ dx$

Si los dos límites de integración de una integral definida coinciden, dicha integral da como resultado cero.

$\displaystyle\int_a^a f(x)\ dx=0$

Sea c un punto interior del intervalo [a,b], la integral definida en el intervalo [a,b] se puede descomponer en dos integrales: una integral definida en el intervalo [a,c] y otra integral definida en el intervalo [c,b].

$\displaystyle\int_a^b f(x)\ dx=\int_a^c f(x)\ dx+\int_c^b f(x)\ dx$

➤ Ver: Métodos de integración