▷ Integrales definidas

En este artículo te explicamos qué es una integral definida. De modo que encontrarás cómo se resuelve una integral definida, integrales definidas resueltas de ejemplo y, además, cuáles son las propiedades de este tipo de integrales.

Índice

¿Qué son las integrales definidas?

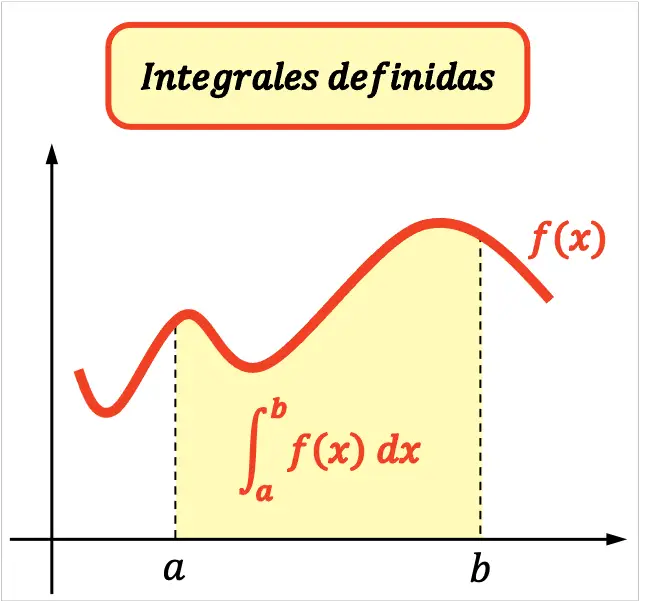
Las integrales definidas son integrales que sirven para calcular el área de la región comprendida entre la función y el eje de abscisas en un intervalo determinado.

La integral definida de la función f(x) en el intervalo [a,b] es igual al área entre la gráfica de f(x), el eje X y las rectas verticales x=a y x=b.

Así pues, las integrales definidas se representan de la siguiente manera:

$\displaystyle\int_a^b f(x)\ dx$

Donde:

$\displaystyle\int$ es el signo de integración.
$\displaystyle a$ es el límite inferior de la integración.
$\displaystyle b$ es el límite superior de la integración.
$\displaystyle f(x)$ es la función a integrar.
$\displaystyle dx$ es el diferencial de x, que indica la variable de la función que se integra.

La principal diferencia entre las integrales definidas y las integrales indefinidas es que las integrales definidas dan como resultado un valor, mientras que el resultado de las integrales indefinidas son funciones.

➤ Ver: Integrales indefinidas

Cómo resolver una integral definida

Para calcular el resultado de una integral definida se debe utilizar la regla de Barrow:

La integral definida de una función continua f(x) en un intervalo [a,b] es igual a la diferencia entre los valores que toma la función primitiva F(x) en los extremos del intervalo, es decir, F(b)-F(a).

Entonces, la fórmula para resolver integrales definidas es la siguiente:

$\displaystyle\int_a^b f(x) \ dx=F(b)-F(a)$

Donde F(x) es la integral de la función f(x).

Por lo tanto, para resolver una integral definida de una función primero se debe integrar dicha función, luego evaluar la función primitiva obtenida de la integral en los extremos del intervalo y, por último, restar los valores obtenidos.

Ejemplo de integral definida

A continuación te dejamos un ejemplo en el que se resuelve una integral definida, así podrás ver cómo se calculan este tipo de integrales.

$\displaystyle\int_1^3 2x\ dx$

Lo primero que debemos hacer para hallar el resultado de esta integral definida es calcular la integral de la función. Así pues, aplicamos la fórmula de la integral de una potencia para resolverla:

$\displaystyle\int_1^3 2x\ dx=\left[\frac{2x^2}{2}\right]_1^3=\left[x^2\right]_1^3$

Ahora evaluamos la función primitiva en los dos extremos del intervalo y restamos los resultados:

$\displaystyle\left[x^2\right]_1^3=3^2-1^2=9-1=8$

Y de este modo hemos conseguido resolver la integral definida:

$\displaystyle\int_1^3 2x\ dx=8$

Ejercicios resueltos de integrales definidas

Ejercicio 1

Resuelve la siguiente integral definida utilizando la regla de Barrow:

$\displaystyle\int_2^4 \left(4x^3+3x^2-5\right)\ dx$

Ver solución

Para evaluar la integral definida tenemos que usar la fórmula de la regla de Barrow:

$\displaystyle\int_2^4 \left(4x^3+3x^2-5\right)\ dx=\left[\frac{4x^4}{4}+\frac{3x^3}{3}-5x\right]_2^4=\left[x^4+x^3-5x\right]_2^4$

Ahora evaluamos la función primitiva en los extremos de la integral:

$\displaystyle\left[x^4+x^3-5x\right]_2^4=4^4+4^3-5\cdot 4-\left(2^4+2^3-5\cdot 2\right)$

Por último, calculamos todas las operaciones resultantes:

$\begin{aligned}&\displaystyle 4^4+4^3-5\cdot 4-\left(2^4+2^3-5\cdot 2\right)=\\[2ex]&=256+64-20-(16+8-10)=\\[2ex]&=300-14=\\[2ex]&=286\end{aligned}$

Ejercicio 2

Calcula el resultado de la siguiente integral definida:

$\displaystyle\int_0^\pi \text{sen}(x)\ dx$

Ver solución

Primero resolvemos la integral trigonométrica del seno:

$\displaystyle\int_0^\pi \text{sen}(x)\ dx=\left[-\text{cos}(x)\right]_0^\pi$

Evaluamos la función del coseno obtenida en los extremos de integración:

$\displaystyle\left[-\text{cos}(x)\right]_0^\pi=-\text{cos}(\pi)-\bigl(-\text{cos}(0)\bigr)=-\text{cos}(\pi)+\text{cos}(0)$

De modo que el resultado de la integral definida es el siguiente:

$-\text{cos}(\pi)+\text{cos}(0)=-(-1)+1=2$

Ejercicio 3

Halla la siguiente integral definida aplicando la regla de Barrow:

$\displaystyle\int_0^{\sqrt{e-1}} \frac{x}{1+x^2}\ dx$

Ver solución

Lo primero que debemos hacer es resolver la integral:

$\displaystyle\int_0^{\sqrt{e-1}} \frac{x}{1+x^2}\ dx=\frac{1}{2}\int_0^{\sqrt{e-1}} \frac{2x}{1+x^2}\ dx=\left[\frac{\ln|1+x^2|}{2}\right]_0^{\sqrt{e-1}}$

Evaluamos el logaritmo neperiano en los extremos del intervalo de integración:

$\displaystyle\left[\frac{\ln|1+x^2|}{2}\right]_0^{\sqrt{e-1}}=\frac{\ln|1+\left(\sqrt{e-1}\right)^2|}{2}-\frac{\ln|1+0^2|}{2}$

Y hacemos todos los cálculos para hallar el resultado de la integral definida:

$\displaystyle\frac{\ln|1+\left(\sqrt{e-1}\right)^2|}{2}-\frac{\ln|1+0^2|}{2}=\frac{\ln|1+e-1|}{2}-\frac{\ln|1|}{2}=\frac{\ln|e|}{2}-0=\frac{1}{2}$

Ejercicio 4

Resuelve la siguiente integral definida por la regla de Barrow:

$\displaystyle\int_0^{\pi/4}\text{sen}(x)\text{cos}(x)\ dx$

Ver solución

Para poder solucionar la integral primero tenemos que transformarla utilizando la siguiente indentidad trigonométrica

$\text{sen}(2x)=2\cdot \text{sen}(x)\text{cos}(x)$

$\displaystyle\int_0^{\pi/4}\text{sen}(x)\text{cos}(x)\ dx=\int_0^{\pi/4}\frac{\text{sen}(2x)}{2}\ dx$

Ahora resolvemos la integral trigonométrica:

$\displaystyle\int_0^{\pi/4}\frac{\text{sen}(2x)}{2}\ dx=\frac{1}{2}\cdot\frac{1}{2}\int_0^{\pi/4} 2\text{sen}(2x)\ dx=\frac{1}{4}\cdot \left[-\text{cos}(2x)\right]_0^{\pi/4}$

Evaluamos el coseno obtenido en los extremos del intervalo:

$\displaystyle\frac{1}{4}\cdot \left[-\text{cos}(2x)\right]_0^{\pi/4}=\frac{1}{4}\cdot \left[-\text{cos}\left(\frac{2\pi}{4}\right)-\bigl(-\text{cos}(2\cdot 0)\bigr)\right]$

Por último, hacemos los cálculos y determinamos el valor de la integral definida:

$\begin{aligned}&\displaystyle\frac{1}{4}\cdot \left[-\text{cos}\left(\frac{2\pi}{4}\right)-\bigl(-\text{cos}(2\cdot 0)\bigr)\right]=\\[2ex]&=\frac{1}{4}\cdot \left[-0-(-1)\right]=\\[2ex]&=\frac{1}{4}\cdot 1 = \frac{1}{4}\end{aligned}$

Propiedades de las integrales definidas

Las integrales definidas tienen las siguientes propiedades:

Si se cambian los límites de integración de la integral definida, el resultado es el mismo pero cambiado de signo.
$\displaystyle\int_a^b f(x)\ dx=-\int_b^a f(x)\ dx$
Si los dos límites de integración de una integral definida coinciden, dicha integral da como resultado cero.
$\displaystyle\int_a^a f(x)\ dx=0$
Sea c un punto interior del intervalo [a,b], la integral definida en el intervalo [a,b] se puede descomponer en dos integrales: una integral definida en el intervalo [a,c] y otra integral definida en el intervalo [c,b].
$\displaystyle\int_a^b f(x)\ dx=\int_a^c f(x)\ dx+\int_c^b f(x)\ dx$
La integral definida de la suma de dos o más funciones es equivalente a la suma de la integral definida en el mismo intervalo de cada función por separado.
$\displaystyle\int_a^b \bigl(f(x)+g(x)\bigr)\ dx=\int_a^b f(x)\ dx+\int_a^b g(x)\ dx$
La integral definida del producto de una constante por una función es igual a la constante multiplicada por la integral definida de la función.
$\displaystyle\int_a^b k\cdot f(x)\ dx=k\int_a^b f(x)\ dx$