▷ Regla de Barrow

En este artículo te explicamos qué es la regla de barrow y para qué sirve esta regla de integrales. Así pues, encontrarás cuál es la fórmula de la regla de Barrow y, además, podrás practicar con ejercicios resueltos paso a paso.

Índice

Fórmula de la regla de Barrow

La regla de Barrow es una regla que sirve para calcular el valor de una integral definida.

La regla de Barrow dice que la integral definida de una función continua f(x) en un intervalo [a,b] es igual a la diferencia entre los valores que toma la función primitiva F(x) en los extremos del intervalo, es decir, F(b)-F(a).

Por lo tanto, la fórmula de la regla de Barrow es la siguiente:

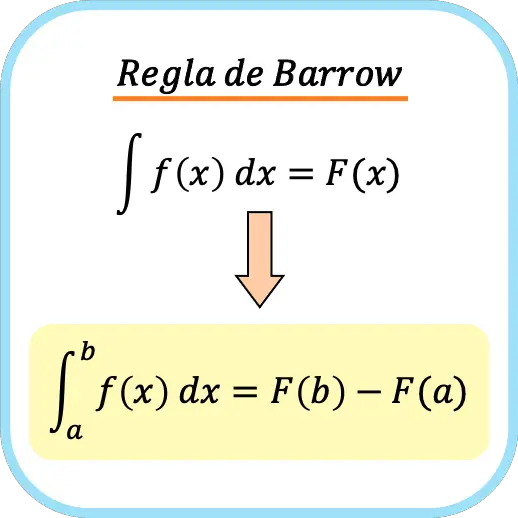
Evidentemente, la regla de Barrow recibe este nombre en honor al matemático inglés Isaac Barrow (1630-1677).

La regla de Barrow también se conoce como segundo teorema fundamental del cálculo o regla de Newton-Leibniz.

Ejemplo de la regla de Barrow

Una vez hemos visto qué dice la regla de Barrow, vamos a ver un ejemplo de su aplicación para acabar de entender su significado.

Calcula el valor de la siguiente integral definida:

$\displaystyle\int_1^3 \left(6x^2+8\right)\ dx$

Para poder evaluar la integral definida en el intervalo [1,3] tenemos que usar la fórmula de la regla de Barrow:

$\displaystyle\int_a^b f(x) \ dx=F(b)-F(a)$

Así pues, primero calculamos la función primitiva:

$\displaystyle\int_1^3 \left(6x^2+8\right)\ dx=\left[\frac{6x^3}{3}+8x\right]_1^3=\left[2x^3+8x\right]_1^3$

Luego evaluamos la función obtenida en los extremos del intervalo:

$\displaystyle\left[2x^3+8x\right]_1^3=2\cdot 3^3+8\cdot 3-\left(2\cdot 1^3+8\cdot 1 \right)$

Y finalmente efectuamos todos los cálculos:

$\begin{aligned}&\displaystyle 2\cdot 3^3+8\cdot 3-\left(2\cdot 1^3}+8\cdot 1 \right)=\\[2ex]&=2\cdot 27+24-\left(2+8 \right)=\\[2ex]&=54+24-10=\\[2ex]&=68\end{aligned}$

Ejercicios resueltos de la regla de Barrow

Ejercicio 1

Resuelve la siguiente integral definida utilizando la regla de Barrow:

$\displaystyle\int_2^4 \left(4x^3+3x^2-5\right)\ dx$

Ver solución

Para evaluar la integral definida tenemos que usar la fórmula de la regla de Barrow:

$\displaystyle\int_2^4 \left(4x^3+3x^2-5\right)\ dx=\left[\frac{4x^4}{4}+\frac{3x^3}{3}-5x\right]_2^4=\left[x^4+x^3-5x\right]_2^4$

Ahora evaluamos la función primitiva en los extremos de la integral:

$\displaystyle\left[x^4+x^3-5x\right]_2^4=4^4+4^3-5\cdot 4-\left(2^4+2^3-5\cdot 2\right)$

Por último, calculamos todas las operaciones resultantes:

$\begin{aligned}&\displaystyle 4^4+4^3-5\cdot 4-\left(2^4+2^3-5\cdot 2\right)=\\[2ex]&=256+64-20-(16+8-10)=\\[2ex]&=300-14=\\[2ex]&=286\end{aligned}$

Ejercicio 2

Calcula la siguiente integral definida mediante la regla de Barrow:

$\displaystyle\int_0^\pi \text{sen}(x)\ dx$

Ver solución

Primero resolvemos la integral trigonométrica del seno:

$\displaystyle\int_0^\pi \text{sen}(x)\ dx=\left[-\text{cos}(x)\right]_0^\pi$

Evaluamos la función del coseno obtenida en los extremos de integración:

$\displaystyle\left[-\text{cos}(x)\right]_0^\pi=-\text{cos}(\pi)-\bigl(-\text{cos}(0)\bigr)=-\text{cos}(\pi)+\text{cos}(0)$

De modo que el resultado de la integral definida es el siguiente:

$-\text{cos}(\pi)+\text{cos}(0)=-(-1)+1=2$

Ejercicio 3

Halla la siguiente integral definida aplicando la regla de Barrow:

$\displaystyle\int_0^{\sqrt{e-1}} \frac{x}{1+x^2}\ dx$

Ver solución

Lo primero que debemos hacer es resolver la integral:

$\displaystyle\int_0^{\sqrt{e-1}} \frac{x}{1+x^2}\ dx=\frac{1}{2}\int_0^{\sqrt{e-1}} \frac{2x}{1+x^2}\ dx=\left[\frac{\ln|1+x^2|}{2}\right]_0^{\sqrt{e-1}}$

Evaluamos el logaritmo neperiano en los extremos del intervalo de integración:

$\displaystyle\left[\frac{\ln|1+x^2|}{2}\right]_0^{\sqrt{e-1}}=\frac{\ln|1+\left(\sqrt{e-1}\right)^2|}{2}-\frac{\ln|1+0^2|}{2}$

Y hacemos todos los cálculos para hallar el resultado de la integral definida:

$\displaystyle\frac{\ln|1+\left(\sqrt{e-1}\right)^2|}{2}-\frac{\ln|1+0^2|}{2}=\frac{\ln|1+e-1|}{2}-\frac{\ln|1|}{2}=\frac{\ln|e|}{2}-0=\frac{1}{2}$

Ejercicio 4

Resuelve la siguiente integral definida por la regla de Barrow:

$\displaystyle\int_0^{\pi/4}\text{sen}(x)\text{cos}(x)\ dx$

Ver solución

Para poder solucionar la integral primero tenemos que transformarla utilizando la siguiente indentidad trigonométrica

$\text{sen}(2x)=2\cdot \text{sen}(x)\text{cos}(x)$

$\displaystyle\int_0^{\pi/4}\text{sen}(x)\text{cos}(x)\ dx=\int_0^{\pi/4}\frac{\text{sen}(2x)}{2}\ dx$

Ahora resolvemos la integral trigonométrica:

$\displaystyle\int_0^{\pi/4}\frac{\text{sen}(2x)}{2}\ dx=\frac{1}{2}\cdot\frac{1}{2}\int_0^{\pi/4} 2\text{sen}(2x)\ dx=\frac{1}{4}\cdot \left[-\text{cos}(2x)\right]_0^{\pi/4}$

Evaluamos el coseno obtenido en los extremos del intervalo:

$\displaystyle\frac{1}{4}\cdot \left[-\text{cos}(2x)\right]_0^{\pi/4}=\frac{1}{4}\cdot \left[-\text{cos}\left(\frac{2\pi}{4}\right)-\bigl(-\text{cos}(2\cdot 0)\bigr)\right]$

Por último, hacemos los cálculos y determinamos el valor de la integral definida:

$\begin{aligned}&\displaystyle\frac{1}{4}\cdot \left[-\text{cos}\left(\frac{2\pi}{4}\right)-\bigl(-\text{cos}(2\cdot 0)\bigr)\right]=\\[2ex]&=\frac{1}{4}\cdot \left[-0-(-1)\right]=\\[2ex]&=\frac{1}{4}\cdot 1 = \frac{1}{4}\end{aligned}$

Fórmula de la regla de Barrow

Ejemplo de la regla de Barrow

Ejercicios resueltos de la regla de Barrow

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Deja un comentario Cancelar respuesta