Integral de una potencia

En este post te explicamos cómo se calcula la integral de una potencia. Así pues, encontrarás la fórmula de la integral de una potencia y varios ejemplos resueltos para poder practicar.

Fórmula de la integral de una potencia

La integral de una potencia de x es igual a x elevado a la potencia más uno dividido por la potencia más uno.

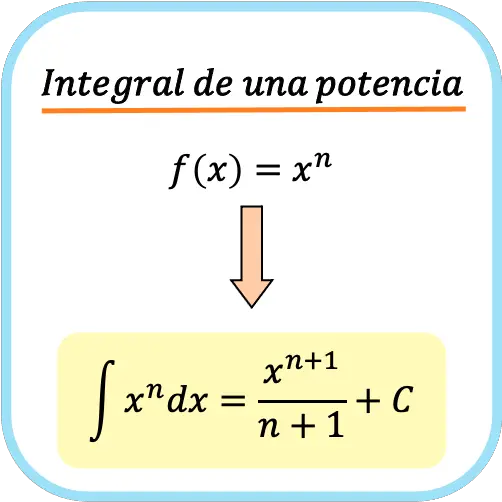
fórmula de la integral de una potencia

Por ejemplo, la integral de x3 es x4/4.

\displaystyle\int x^3dx=\cfrac{x^{3+1}}{3+1}+C=\cfrac{x^4}{4}+C

Ten en cuenta que esta fórmula solo se puede utilizar cuando calculamos la integral de un monomio, es decir, cuando la base de la potencia es simplemente una x. Si tenemos un polinomio en la base debemos hacer un paso previo antes de aplicar la fórmula, más abajo veremos cómo se hace.

➤ Ver: Derivada de una potencia

Ejemplos de integrales de potencias

Una vez hemos visto cuál es la fórmula de la integral de una potencia, vamos a ver varios ejemplos de este tipo de integrales para que puedas entender bien cómo se integran las funciones potenciales.

Ejemplo 1: Integral de x elevado a la dos

\displaystyle\int x^2dx

Tal y como hemos visto arriba, la fórmula para hallar integral de una potencia de base x es la siguiente:

\displaystyle\int x^ndx=\cfrac{x^{n+1}}{n+1}+C

Por lo tanto, la integral de x elevado al cuadrado es igual a x a la tres partido por tres.

\displaystyle\int x^2dx=\cfrac{x^{2+1}}{2+1}+C=\cfrac{x^3}{3}+C

Ejemplo 2: Integral de una potencia negativa

\displaystyle\int x^{-5}dx

Aunque la potencia sea negativa, la fórmula que debemos usar para determinar su integral es la misma:

\displaystyle\int x^ndx=\cfrac{x^{n+1}}{n+1}+C

Así pues, el resultado de la integral de esta potencia negativa es el siguiente:

\displaystyle\int x^{-5}dx=\cfrac{x^{-5+1}}{-5+1}+C=\cfrac{x^{-4}}{-4}+C

Ejemplo 3: Integral de la potencia de un binomio

\displaystyle\int\left(x+4\right)^2dx

En este caso no podemos utilizar directamente la fórmula de la integral de una potencia, pues la base es un polinomio con dos términos, sino que primero tenemos que hacer un cambio de variable:

x+4=u

dx=du

Así pues, tras aplicar el cambio de variable la integral queda de la siguiente manera:

\displaystyle\int\left(x+4\right)^2dx=\int u^2du

Ahora sí que podemos utilizar la fórmula de la integral de una potencia:

\displaystyle\int u^2du=\cfrac{u^3}{3}+C

Y, por último, deshacemos el cambio de variable:

\displaystyle \cfrac{(x+4)^3}{3}+C

➤ Ver: Integración por sustitución o cambio de variable

Ejercicios resueltos de integrales de potencias

Calcula las integrales de las siguientes potencias:

\text{A) }\displaystyle\int 1 dx

\text{B) }\displaystyle\int 5x dx

\text{C) }\displaystyle\int x^3 dx

\text{D) }\displaystyle\int 7x^6 dx

\text{E) }\displaystyle\int \cfrac{x^5}{10} \cdot dx

\text{F) }\displaystyle\int \sqrt{x^5} dx

\text{G) }\displaystyle\int \left(7x+4)^3 dx

\text{A) }\displaystyle\int 1 dx=\int x^0 dx=\cfrac{x^1}{1}+C=x+C

\text{B) }\displaystyle\int 5x dx=5\int x dx = \cfrac{5x^2}{2}+C

\text{C) }\displaystyle\int x^3 dx=\cfrac{x^4}{4}+C

\text{D) }\displaystyle\int 7x^6 dx =7\int x^6 dx = \cfrac{7x^7}{7}=x^7+C

\text{E) }\displaystyle\int \cfrac{x^5}{10}\cdot dx=\cfrac{1}{10}\int x^5 dx= \cfrac{5x^6}{10\cdot 6}+C=\cfrac{x^6}{12}+C

\text{F) }\displaystyle\int \sqrt{x^5} dx=\int x^{5/2} dx= \cfrac{x^{5/2+1}}{\frac{5}{2}+1}+C=\cfrac{x^{7/2}}{\frac{7}{2}}+C=\cfrac{2x^{7/2}}{7}+C

\text{G) }\displaystyle\int \left(7x+4\right)^3 dx=\int u^3 \cdot \cfrac{1}{7}\cdot du=\cfrac{u^4}{7\cdot 4}+C=\cfrac{ \left(7x+4\right)^4}{28}+C

 

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *