▷ Derivada de una potencia (fórmula y ejercicios resueltos)

Aquí te explicamos cómo derivar una potencia (o función potencial), encontrarás la fórmula de la derivada de una potencia, varios ejemplos e incluso podrás practicar con ejercicios resueltos paso a paso.

Índice

Fórmula de la derivada de una potencia

La derivada de una potencia, o función potencial, es el producto del exponente de la potencia por la base elevada al exponente menos 1 por la derivada de la base.

$f(x)=u^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot u^{k-1}\cdot u'$

Por lo tanto, si la base es la función identidad, para derivar la potencia solamente tenemos que multiplicar la función por el exponente y restarle una unidad al exponente:

$f(x)=x^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot x^{k-1}$

Esto es debido a que la derivada de la función identidad es igual a 1.

En resumen, para derivar una función potencial existen dos fórmulas: la primera que se puede utilizar siempre y la segunda que solo se puede aplicar cuando la base es una x.

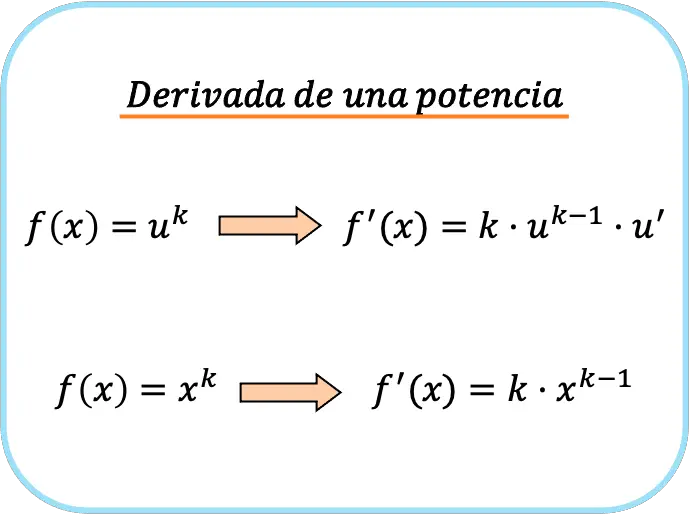
Se puede comprobar fácilmente que la primera fórmula mostrada de la derivada de una potencia es como la segunda pero aplicando la regla de la cadena.

Cabe destacar que estas fórmulas solo se pueden utilizar cuando la variable es la base de la potencia, si la x está en el denominador debes aplicar la regla de la derivada de una función exponencial:

➤ Ver: derivada de una función exponencial

Ejemplos de derivadas de potencias

Una vez hemos visto la fórmula de la derivada de una función potencial, vamos a explicar varios ejemplos de este tipo de derivadas para que te quede claro cómo se derivan las potencias.

Ejemplo 1: Derivada de una potencia de base x

$f(x)=x^4$

Tal y como hemos explicado en el apartado anterior, cuando la base de la potencia es solamente una x, la fórmula que debemos usar para derivar la función es la siguiente:

$f(x)=x^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot x^{k-1}$

De modo que la derivada de la potencia x elevada a 4 es:

$f(x)=x^4 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=4\cdot x^{4-1}=4x^3$

Ejemplo 2: Derivada de una potencia con paréntesis

$f(x)=(2x-1)^5$

En este ejemplo la base no es la función identidad, por lo que debemos emplear la fórmula general de la derivada de una potencia:

$f(x)=u^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot u^{k-1}\cdot u'$

La función de dentro del paréntesis es una función lineal, así que su derivada es 2. Por lo tanto, la derivada de toda la función potencial es:

$f(x)=(2x-1)^5 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=5\cdot (2x-1)^4\cdot 2=10(2x-1)^4$

Ejemplo 3: Derivada de una potencia negativa

$f(x)=(\log 9x)^{-2}$

En este caso tenemos una función potencial cuyo exponente es negativo y cuya base es un logaritmo, así que utilizaremos la siguiente fórmula para derivar la función:

$f(x)=u^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot u^{k-1}\cdot u'$

Aunque el exponente de la potencia sea negativo, también debemos restarle uno. Por lo tanto, la derivada de la función es:

$f'(x)=-2\cdot (\log 9x)^{-3}\cdot \cfrac{1}{9x\cdot \ln 10}\cdot 9 =\cfrac{-2(\log 9x)^{-3}}{x\ln 10}$

Si tienes dudas de la resolución, puedes consultar la fórmula de la derivada de una función logarítmica aquí:

➤ Ver: derivada de una función logarítmica

Ejemplo 4: Derivada de una potencia con raíz

$f(x)=\sqrt[3]{(5x+2)^7}$

La función de este ejemplo es una potencia dentro de una expresión racional. Sin embargo, los radicales se pueden transformar en expresiones potenciales, por lo tanto, la función se puede simplificar convirtiéndola en una función potencial con exponente fraccionario:

$f(x)=(5x+2)^{\frac{7}{3}}$