Funciones no lineales

En este post encontrarás qué son las funciones no lineales. También explicamos las diferencias entre las funciones lineales y las funciones no lineales. Y, además, podrás ver cuáles son los distintos tipos de funciones no lineales con ejemplos.

¿Qué es una función no lineal?

Una función no lineal es aquella función cuya representación gráfica no es una línea recta, sino que tiene cualquier otra forma.

Por lo tanto, las funciones polinómicas de primer grado son las únicas que no son funciones no lineales.

¿Cuáles son las diferencias entre una función lineal y una función no lineal?

La principal diferencia entre una función lineal y una función no lineal es su representación gráfica, ya que las gráficas de todas las funciones lineales son líneas rectas, en cambio, las gráficas de las funciones no lineales pueden tener cualquier forma: parábolas, curvas cúbicas, hipérboles, etc.

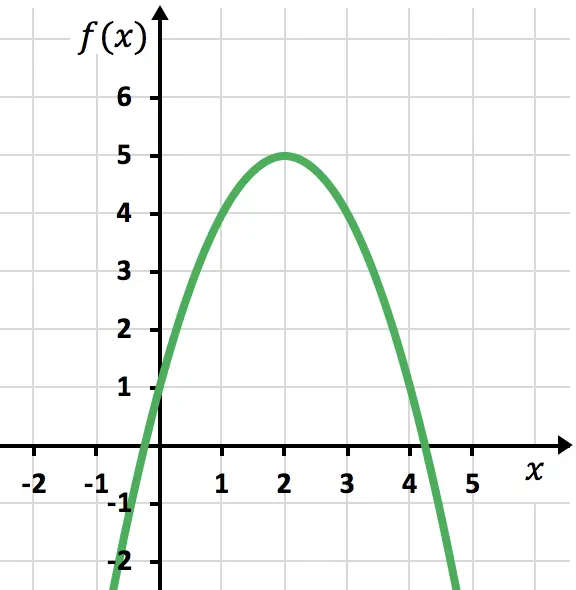
A continuación, puedes ver representada gráficamente una función no lineal y una función lineal:

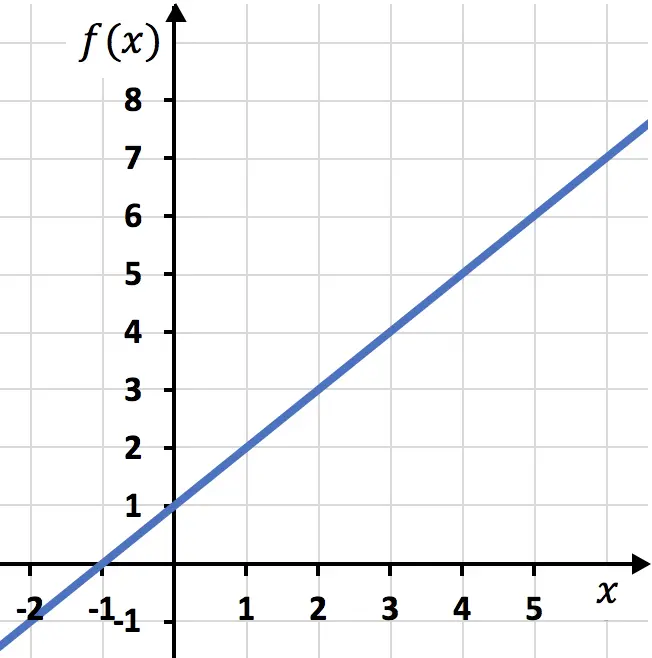
Otra distinción entre estos dos tipos de funciones es el grado. Las funciones lineales siempre son de primer grado, pero las funciones no lineales pueden ser de segundo grado, de tercer grado, de cuarto grado, etc.

Las funciones lineales y las no lineales también se diferencian en la continuidad. Porque las funciones lineales siempre son continuas en todo su dominio y, por otro lado, las funciones no lineales pueden presentar algún tipo de discontinuidad.

Puedes saber más al respecto en el siguiente enlace:

➤ Ver: ¿qué son las funciones lineales?

Tipos de funciones no lineales

Una vez hemos visto la definición de función no lineal, vamos a ver cuáles son todos los tipos de funciones no lineales.

Funciones cuadráticas

Una función cuadrática es una función polinómica de segundo grado, o dicho de otra forma, es una función en la que el exponente más grande es 2.

Por lo tanto, la fórmula de una función cuadrática es la siguiente:

Donde es el término cuadrático, el término lineal y el término independiente de la función polinómica.

Ejemplos de funciones cuadráticas o funciones polinómicas de segundo grado:

Representar una función cuadrática en un gráfico es relativamente sencillo y, además, siempre es una parábola. Sin embargo, la forma de la parábola depende del signo del coeficiente principal de la función. Puedes ver cómo se representa es tipo de función no lineal en el siguiente enlace:

➤ Ver: graficar funciones cuadráticas

Funciones de proporcionalidad inversa

Una función de proporcionalidad inversa es aquella función que relaciona dos magnitudes que son inversamente proporcionales.

Nota: dos magnitudes son inversamente proporcionales si una aumenta cuando la otra disminuye y viceversa

Este tipo de funciones no lineales vienen definidas por la siguiente fórmula:

Donde es una constante llamada razón de proporcionalidad.

Ejemplos de funciones de proporcionalidad inversa:

Las funciones de proporcionalidad inversa son más difíciles de representar, ya que siempre tienen asíntotas. Puedes ver cómo se hace en el siguiente enlace:

➤ Ver: representación de funciones de proporcionalidad inversa

Funciones irracionales

Una función irracional, también llamada función radical, es una función no lineal que tiene la variable independiente x bajo el símbolo de una raíz.

Como ya sabes, el resultado de una raíz puede ser positivo o negativo. De manera que la representación de una función irracional (o radical) tiene dos posibles curvas, aunque normalmente se es representa solo la rama positiva.

➤ Ver: representación gráfica de funciones irracionales

Funciones exponenciales

Las funciones exponenciales son aquellas funciones no lineales en las que la variable independiente x aparece en el exponente de una potencia. Es decir, una función exponencial es de la siguiente forma:

Donde es un número real positivo y diferente de 1.

Tal y como su propio nombre indica, la gráfica de una función exponencial crece exponencialmente, así que hay que calcular más puntos de la función para representarla correctamente.

➤ Ver: representación gráfica de funciones exponenciales

Funciones logarítmicas

Las funciones logarítmicas son aquellas funciones cuya variable independiente x forma parte del argumento de un logaritmo. Es decir, una función logarítmica es una función no lineal que presenta la siguiente forma:

Donde es obligatoriamente un número real positivo y diferente de 1.

La inversa de la función logarítmica es la función exponencial. De modo que las gráficas de una función logarítmica y una función exponencial son simétricas respecto de la recta y=x si ambas poseen la misma base.

➤ Ver: representación gráfica de funciones logarítmicas