Función de proporcionalidad inversa

En esta página se explica qué son las funciones de proporcionalidad inversa y cómo hacer su representación gráfica. Además, encontrarás todas las características de este tipo de funciones, cómo calcular su dominio y también varios ejemplos y ejercicios resueltos paso a paso para practicar.

¿Qué es una función de proporcionalidad inversa?

De manera que las funciones de proporcionalidad inversa siempre están compuestas por fracciones con un polinomio de primer grado en el denominador. Por lo tanto, son un tipo de función racional.

Ejemplos de funciones de proporcionalidad inversa:

Normalmente suele ser la variable independiente e la variable dependiente, o dicho con otras palabras, la variable depende de

Por otro lado, la razón de proporcionalidad (el término del numerador) puede ser positiva o negativa y su signo marca el crecimiento o decrecimiento de la función:

• Si la constante es negativa, la función es creciente.
• En cambio, si la constante es positiva, la función es decreciente.

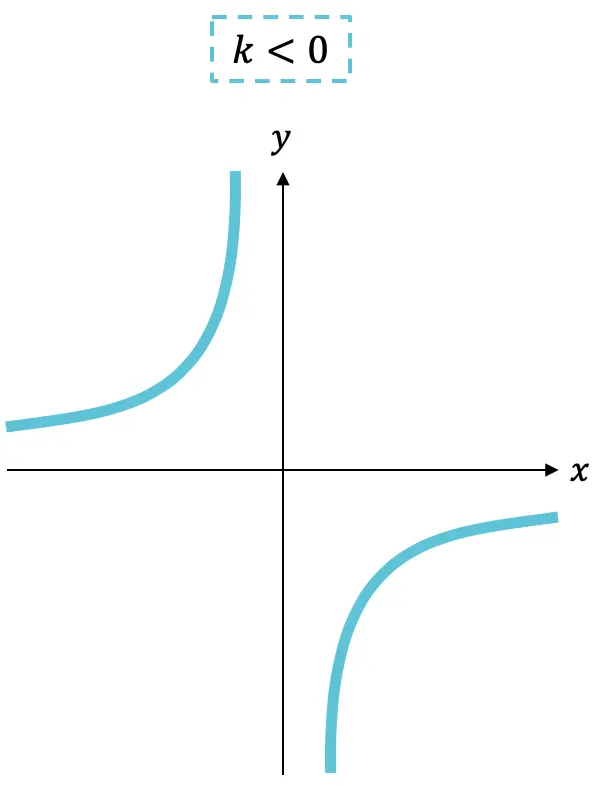
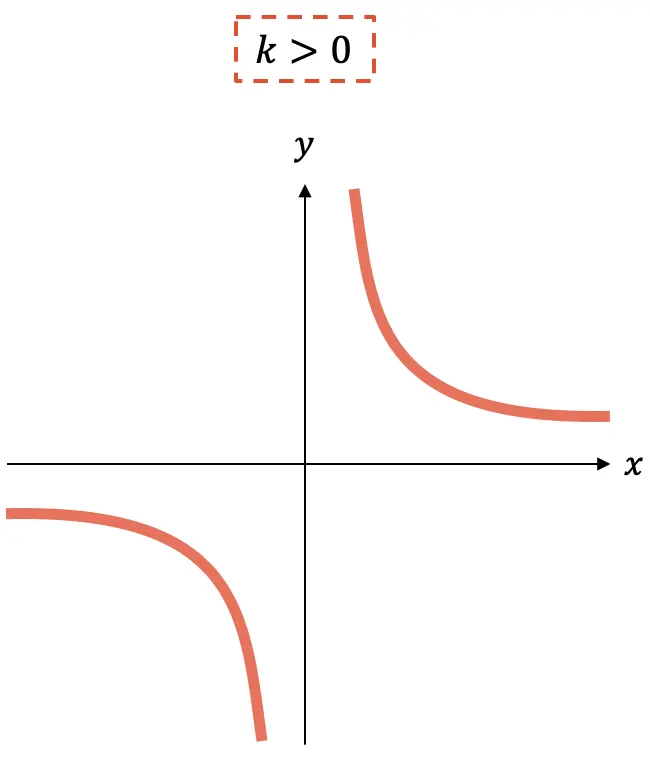
Como puedes ver, la gráfica de una función de proporcionalidad inversa siempre son dos hipérbolas que, dependiendo del signo de k, estarán en un cuadrante u otro.

Dominio de una función de proporcionalidad inversa

Al ser un tipo de función racional, el dominio de una función de proporcionalidad inversa son todos los números reales excepto aquellos que anulan el denominador. Porque el denominador nunca puede ser cero ya que entonces daría infinito como resultado.

A modo de ejemplo, vamos a determinar el dominio de la siguiente función de proporcionalidad inversa:

Para saber cuándo se anula el denominador, debemos igualar su expresión a 0 y resolver la ecuación:

Por lo tanto, cuando x tome el valor de 1 el denominador será cero y obtendremos una indeterminación. Así que el dominio de la función son todos los números reales menos

Cómo representar una función de proporcionalidad inversa

Vamos a ver cómo representar gráficamente una función de proporcionalidad inversa mediante un ejemplo.

• Representaremos en un gráfico la siguiente función:

Lo primero que debemos hacer es hallar el dominio de la función. Al ser una fracción, el denominador nunca puede ser 0, ya que entonces daría infinito como resultado. Por tanto, el dominio serán todas las x menos cuando se anule el denominador. 

Así que igualamos el denominador a 0 para ver qué x no pertenece al dominio:

Por tanto el dominio de la función son todos los números excepto 2:

Una vez sabemos qué número no pertenece al dominio, creamos una tabla de valores. Para representar funciones de proporcionalidad inversa, debemos calcular 3 o 4 puntos a la izquierda y 3 o 4 puntos a la derecha del número que no pertenece al dominio (2):

Ahora representamos los puntos en un gráfico:

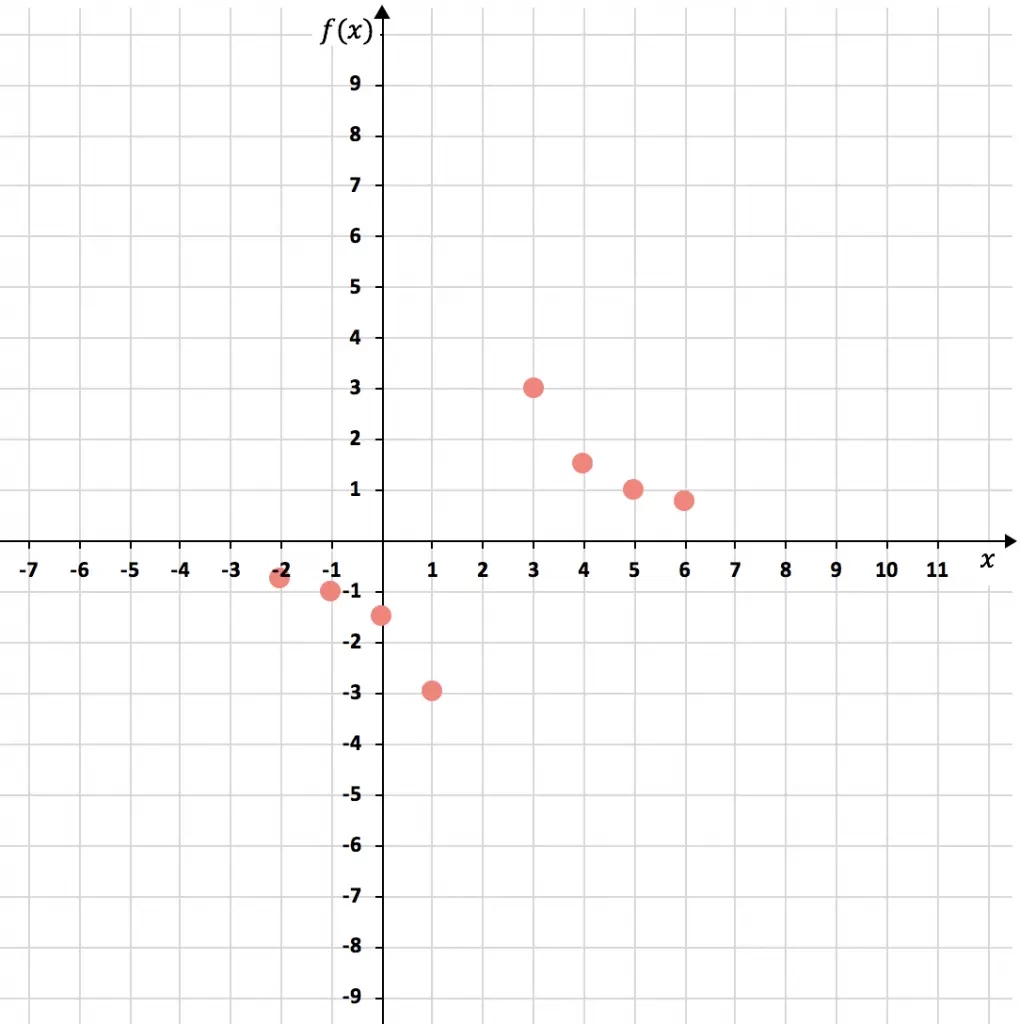
Y finalmente unimos los puntos, formando las dos hipérbolas de la función de proporcionalidad inversa. Además, alargamos las ramas de las hipérbolas para indicar que siguen creciendo:

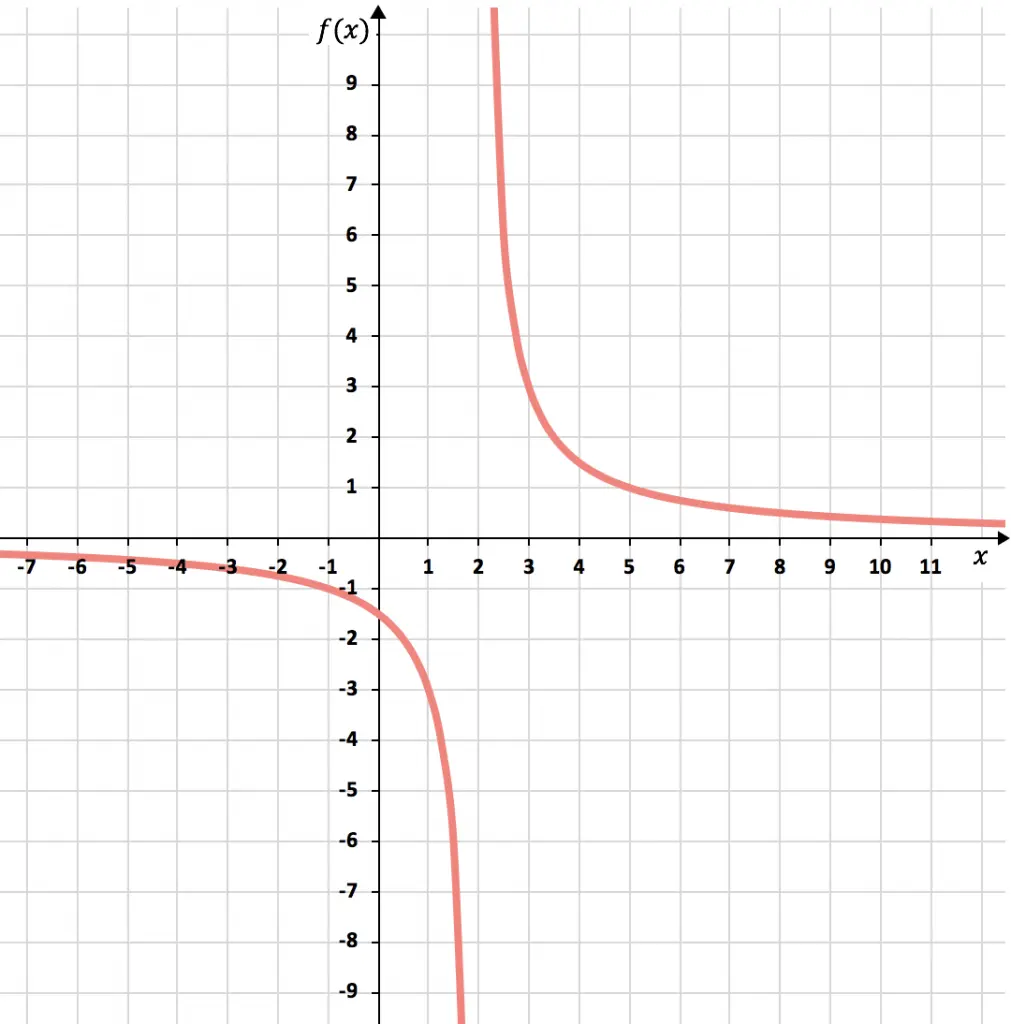
Fíjate que la función se va acercando a , tanto por la derecha como por la izquierda. Sin embargo, nunca llega a tocar el 2, se aproxima mucho pero nunca lo llega a tocar. Por lo tanto, se trata de una asíntota vertical. Eso es porque no pertenece al dominio de la función y, en consecuencia, la función no existe en ese punto.

Y lo mismo sucede con el eje horizontal X. La función se va acercando a , pero nunca lo llega a tocar. Por tanto,  es una asíntota horizontal.

Esto significa que todas las funciones de proporcionalidad inversa son discontinuas, ya que siempre tienen alguna asíntota.

Puedes consultar más sobre asíntotas y límites de funciones en nuestra web.

Ejercicios resueltos de funciones de proporcionalidad inversa

Ejercicio 1

Calcula el dominio de la siguiente función de proporcionalidad inversa:

Una función de proporcionalidad inversa no existirá cuando el denominador sea 0, ya que entonces la función daría ∞. Por tanto, tenemos que igualar a 0 el denominador de la función para ver qué x anula el denominador y, en consecuencia, no pertenece al dominio.

 

Ejercicio 2

Representa en una gráfica la siguiente función de proporcionalidad inversa:

Lo primero que debemos hacer es calcular el dominio de la función:

Una vez sabemos qué número no pertenece al dominio, creamos una tabla de valores con la función:

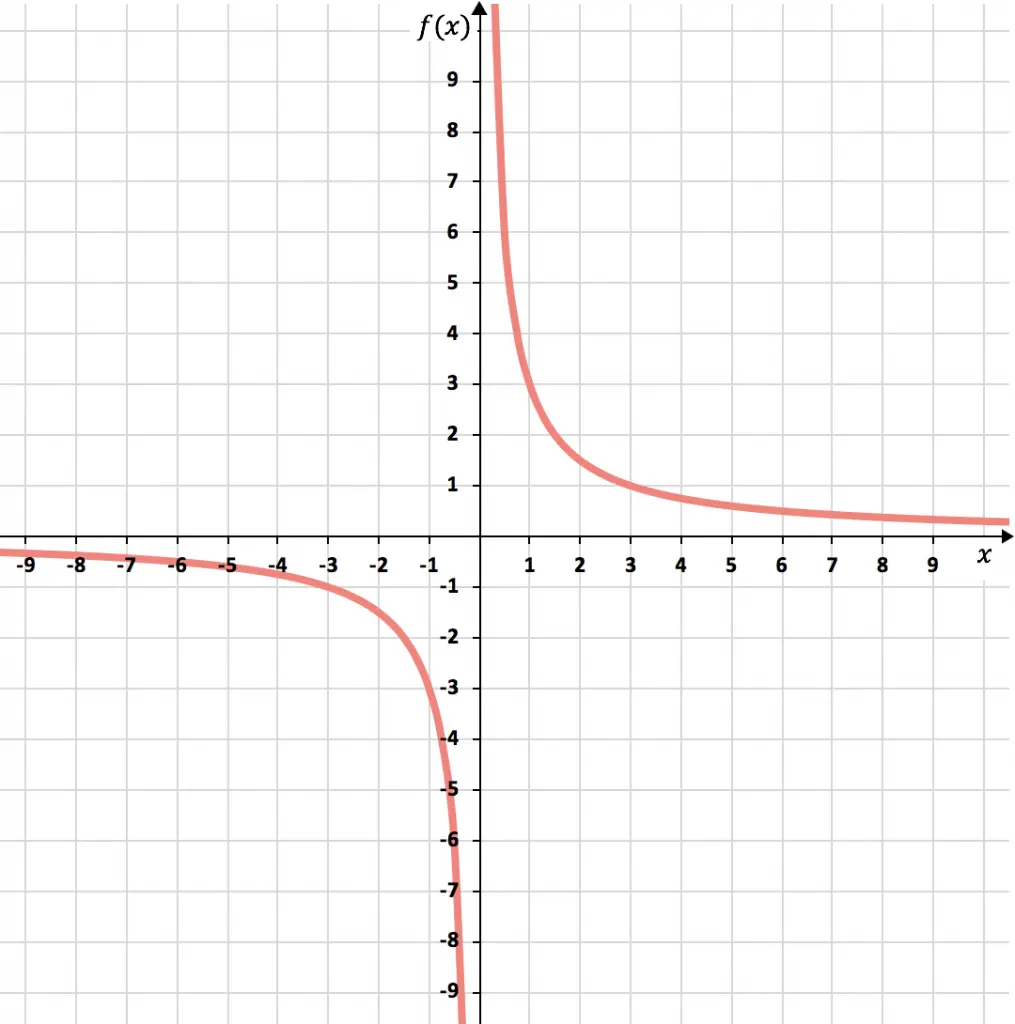
Finalmente, representamos los puntos obtenidos en la gráfica y trazamos las hipérbolas, formando así la función de proporcionalidad inversa:

 

Ejercicio 3

Representa en un gráfico la siguiente función de proporcionalidad inversa:

Lo primero que debemos hacer es calcular el dominio de la función:

Una vez conocemos el dominio de la función, construimos una tabla de valores:

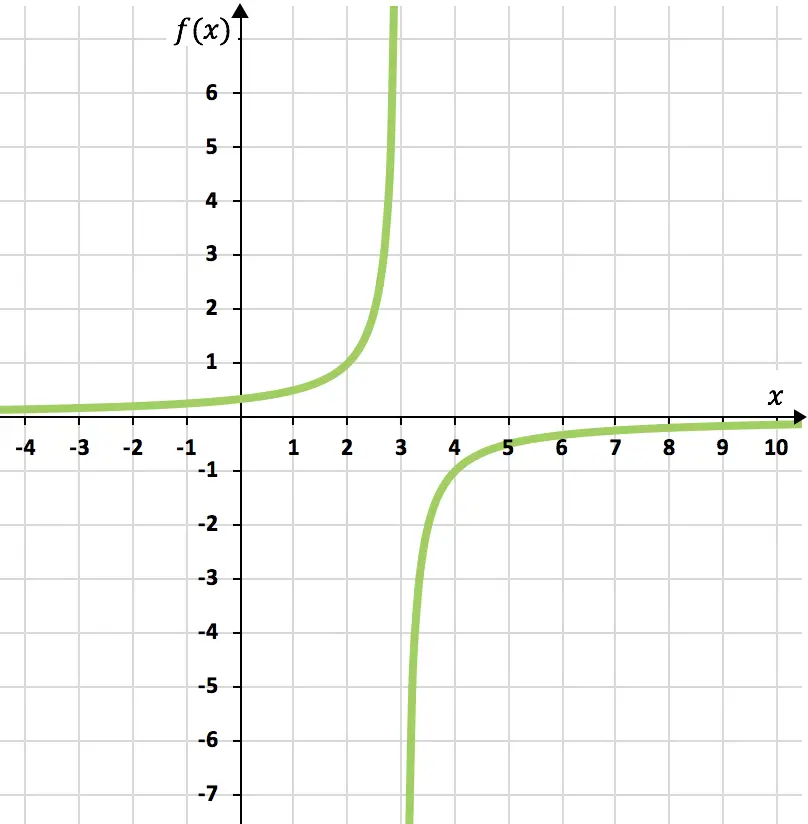
Por último, representamos los puntos obtenidos en una gráfica y trazamos las hipérbolas, formando así la función de proporcionalidad inversa:

 

Ejercicio 4

Realiza la representación gráfica de la siguiente función de proporcionalidad inversa:

Primero de todo, tenemos que calcular el dominio de la función:

Una vez sabemos cuál es el dominio de la función, hacemos una tabla de valores:

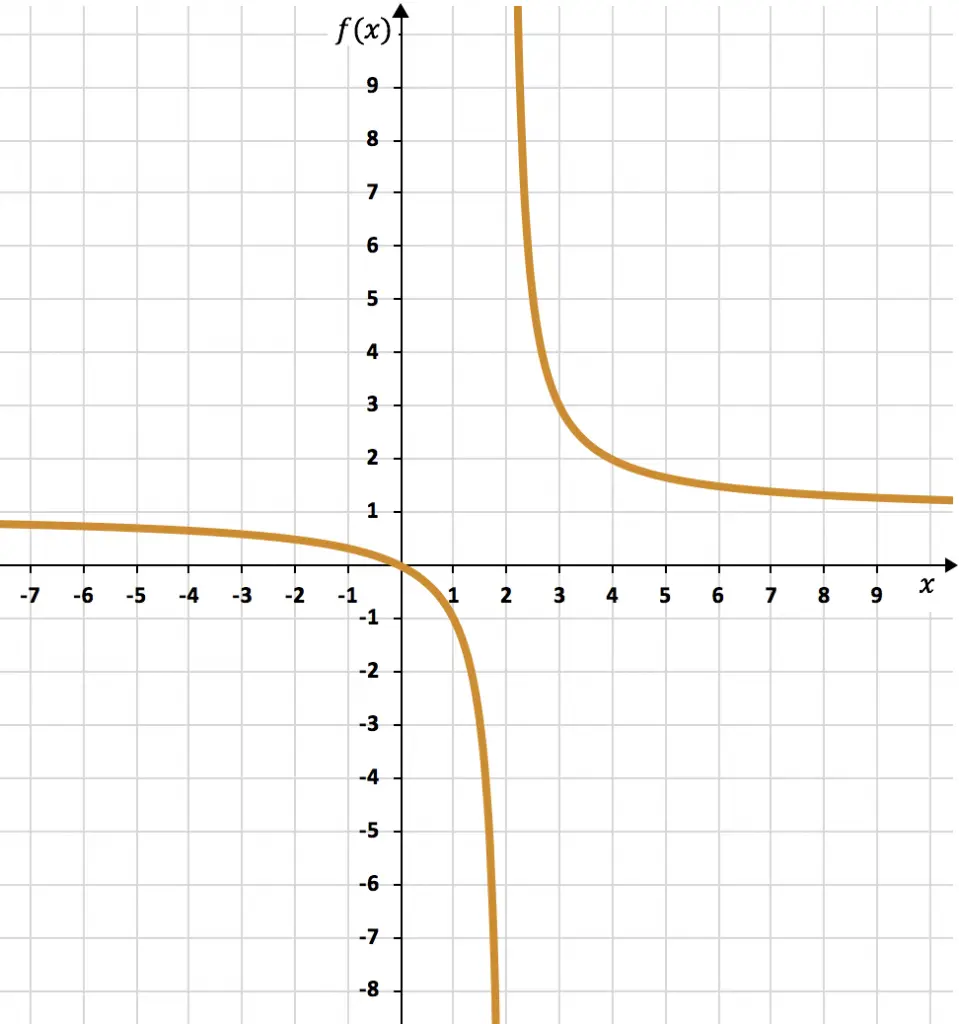
Y, para finalizar, representamos los puntos obtenidos en una gráfica y dibujamos las hipérbolas, formando así la función de proporcionalidad inversa:

 

Ejercicio 5

Representa en la gráfica la siguiente función racional:

Lo primero que debemos hacer es calcular el dominio de la función:

Una vez conocemos el dominio de la función, construimos una tabla de valores:

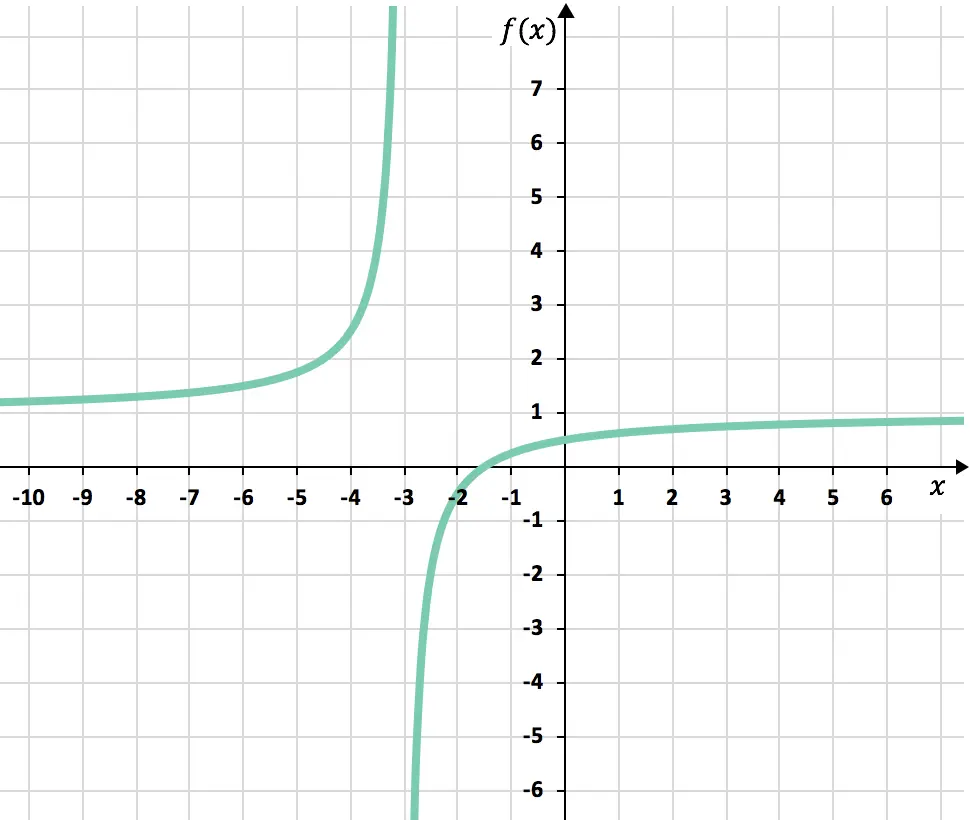
Para acabar, solo nos falta representar los puntos obtenidos en una gráfica y trazar las hipérbolas, formando así la función de fraccionaria:

 

Aplicaciones de la función de proporcionalidad inversa

La función de proporcionalidad inversa aparece en muchos casos de la física y las matemáticas.

Por ejemplo, sirve para describir la relación que hay entre la presión y el volumen en un gas ideal sometido a una temperatura k constante. Esta función se denomina ley de Boyle-Mariotte (P×V=k) y es un ejemplo de función de proporcionalidad inversa. Evidentemente, el dominio de definición de esta función se restringe tan solo a la rama positiva, ya que no existen volúmenes ni presiones negativos.

La relación entre la intensidad de corriente y la resistencia eléctrica sometida a una diferencia de potencial constante también viene regida por una función de proporcionalidad inversa. Esta función es conocida como la ley de Ohm (V=I×R).