▷ Función Irracional (o Radical): dominio, representación gráfica, ejercicios,...

En esta página se explica qué es una función irracional, también llamada función radical, junto con todas las características de este tipo funciones. También encontrarás cómo calcular el dominio de las funciones radicales o irracionales y, además, podrás ver cómo representarlas en una gráfica con ejemplos y practicar con ejercicios y problemas resueltos paso a paso.

Índice

¿Qué es una función irracional (o radical)?

Una función irracional significa lo mismo que una función radical y, por tanto, comparten definición:

Una función irracional, también conocida como función radical, es una función que tiene la variable independiente x bajo el símbolo de una raíz.

Como ya sabemos, el resultado de una raíz puede ser positivo o negativo. De manera que la representación de una función irracional (o radical) tiene dos posibles curvas:

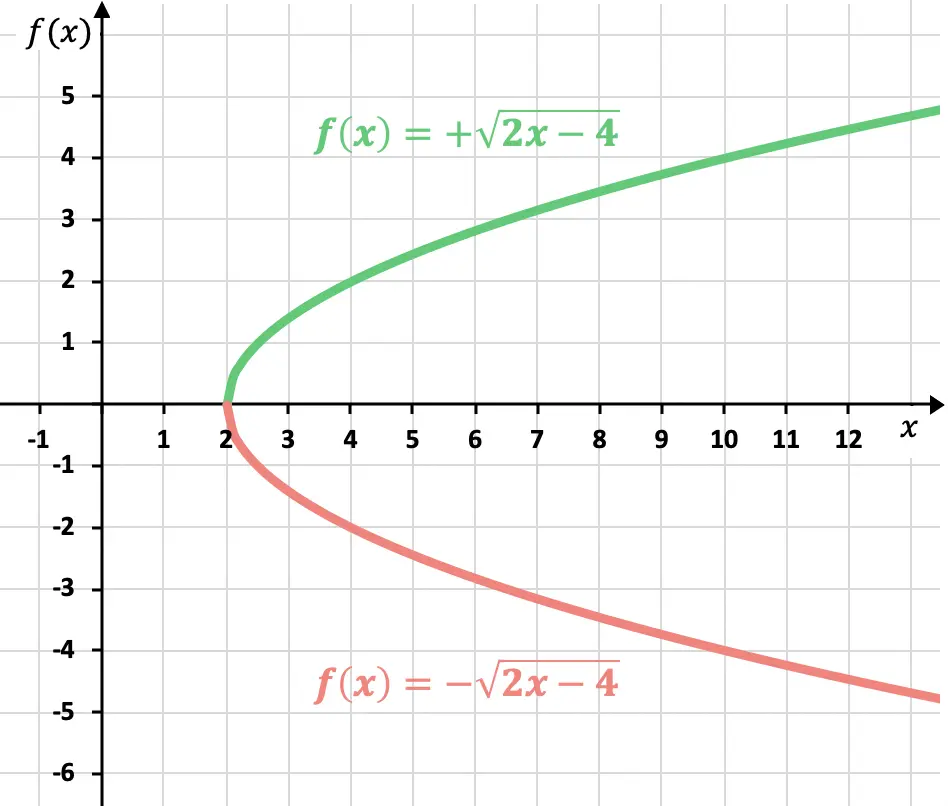
ejemplos de funciones irracionales o radicales

Pero si no se especifica el signo, se supone que se debe representar la función positiva.

Por otro lado, no se debe confundir una función irracional con una función racional. Aunque tengan nombres muy parecidos, son dos tipos de funciones totalmente diferentes.

Dominio de una función irracional o radical

El dominio de una función con raíces depende de la paridad del índice de la raíz, es decir, depende de si el índice del radical es par o impar.

Dominio de una función con raíz de índice par

Como bien sabes, no existe la raíz (de índice par) de un número negativo. Por tanto, una función radical con índice par existirá siempre que su contenido sea igual o más grande que 0.

A modo de ejemplo, veamos cómo se calcula el dominio de la siguiente función radical o irracional:

$f(x)=\sqrt{x-4}$

Consiste en una función radical de índice par, por tanto, debemos mirar cuándo su contenido es positivo o nulo:

$x-4\ge 0$

Resolvemos la inecuación:

$x\ge 4$

De manera que la función existirá siempre que x sea mayor o igual que 4, y se indica con el siguiente intervalo:

$\text{Dom } f= [4,+\infty)$

Dominio de una función con raíz de índice impar

Las funciones irracionales de índice impar no tienen este problema, ya que sí que existe la raíz de índice impar de un número negativo:

$\sqrt[3]{-8}=-2$

En consecuencia, las funciones radicales de índice impar existen por cualquier valor de x. O, dicho con otras palabras, el dominio son todos los números reales.

Por ejemplo, vamos a calcular el dominio de la siguiente función radical cuyo índice es impar:

$f(x)=\sqrt[3]{3x-4}$

Como se trata de una función irracional con índice impar, su dominio son todos los números reales:

$\text{Dom } f= \mathbb{R}$

Cómo representar una función irracional o radical

Vamos a ver cómo representar una función con raíces en un gráfico mediante un ejemplo.

Representa en una gráfica la siguiente función radical o irracional:

$f(x)=\sqrt{x+2}$

Lo primero que debemos hacer es hallar el dominio de la función. Como es una raíz cuadrada, lo de dentro tiene que ser positivo, ya que no existen las raíces cuadradas de un número negativo. Por tanto, la función radical existirá siempre que su contenido sea igual o más grande que 0:

$x+2\ge 0$

$x\ge -2$

De manera que el dominio de la función son todos los números más grandes o iguales que -2. Es decir:

$\text{Dom } f = [-2,+\infty)$

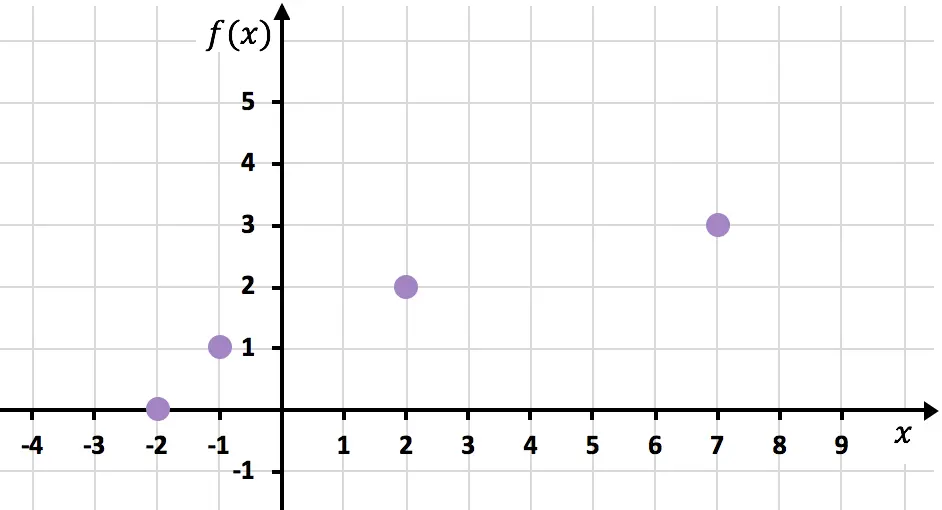
Una vez sabemos el dominio de la función, creamos una tabla de valores. Obviamente, cuantos más puntos calculemos, más precisa será la representación de la función. Pero calculando 3 o 4 puntos dentro del intervalo del dominio es suficiente:

$x= -2 \ \longrightarrow \ f(-2)=\sqrt{-2+2}= 0$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{-1+2}= 1$

$x= 2 \ \longrightarrow \ f(2)=\sqrt{2+2}= 2$

$x= 7 \ \longrightarrow \ f(7)=\sqrt{7+2}= 3$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 0 \\ -1 & 1 \\ 2 & 2 \\ 7 & 3 \end{array}$

Ahora representamos los puntos obtenidos en un gráfico:

como representar una funcion radical o irracional

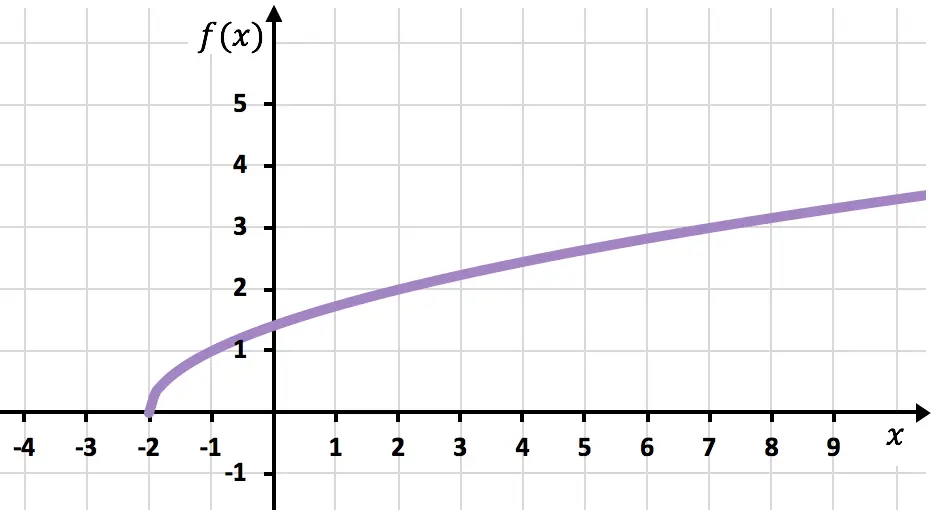
Y, finalmente, unimos los puntos y alargamos la curva para indicar que la función sigue creciendo:

ejemplo de representacion grafica de una funcion radical o irracional

Ejercicios resueltos de funciones irracionales o radicales

Ejercicio 1

Halla el dominio de la siguiente función radical:

$\sqrt{3x+6}$

Ver solución

La raíz cuadrada de un número negativo no existe. Por lo tanto, la función existirá cuando el argumento de la raíz sea positivo o nulo:

$3x+6 \ge 0$

$3x \ge -6$

$x \ge \cfrac{-6}{3}$

$x \ge -2$

$\mathbf{Dom } \ \bm{f = [-2,+\infty)}$

Ejercicio 2

Encuentra el dominio de la siguiente función irracional:

$\sqrt{-x+2}$

Ver solución

La raíz cuadrada de un número negativo no tiene solución real. Por lo tanto, la función existirá siempre que el contenido de la raíz sea positivo o cero:

$-x+2\ge 0$

$-x\ge -2$

$x\le\cfrac{-2}{-1}=2$

Recuerda que si en una inecuación cambiamos de lado un número negativo que está multiplicando o dividiendo también hay que girar el signo de la inecuación.

$x\le2$

$\mathbf{Dom } \ \bm{f = (-\infty,2]}$

Ejercicio 3

Representa en un gráfico la siguiente función irracional:

$f(x)= \sqrt{x-1}$

Ver solución

Antes de nada, tenemos que calcular el dominio de la función:

$x-1\ge 0$

$x\ge 1$

$\text{Dom } f = [1,+\infty)$

Ahora creamos una tabla de valores otorgando a la función valores de dentro del intervalo del dominio:

$x= 1 \ \longrightarrow \ f(1)= \sqrt{1-1}=0$

$x= 2 \ \longrightarrow \ f(2)= \sqrt{2-1}=1$

$x= 5 \ \longrightarrow \ f(5)= \sqrt{5-1}=2$

$x= 10 \ \longrightarrow \ f(10)= \sqrt{10-1}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 2 & 1 \\ 5 & 2 \\ 10 & 3 \end{array}$

Finalmente, representamos los puntos y trazamos la función en la gráfica:

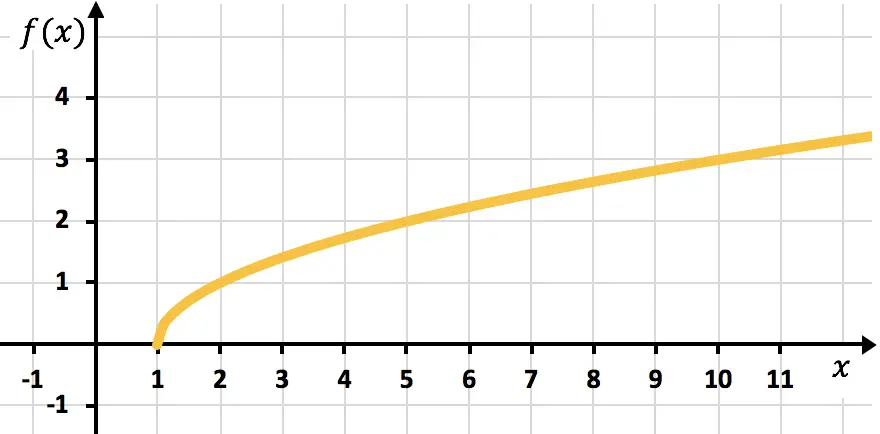
ejercicio resuelto paso a paso de funcion irracional o radical

Ejercicio 4

Representa gráficamente la siguiente función irracional o radical:

$f(x)= -2\sqrt{x}+3$

Ver solución

En primer lugar, debemos calcular el dominio de la función:

$x\ge 0$

$\text{Dom } f = [0,+\infty)$

Ahora creamos una tabla de valores otorgando a la función valores de dentro del intervalo del dominio:

$x= 0 \ \longrightarrow \ f(0)= -2\sqrt{0}+3=3$

$x= 1 \ \longrightarrow \ f(1)= -2\sqrt{1}+3=1$

$x= 4 \ \longrightarrow \ f(4)= -2\sqrt{4}+3=-1$

$x= 9 \ \longrightarrow \ f(9)= -2\sqrt{9}+3=-3$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 3 \\ 1 & 1 \\ 4 & -1 \\ 9 & -3 \end{array}$

Para finalizar, representamos los puntos y dibujamos la función en la gráfica:

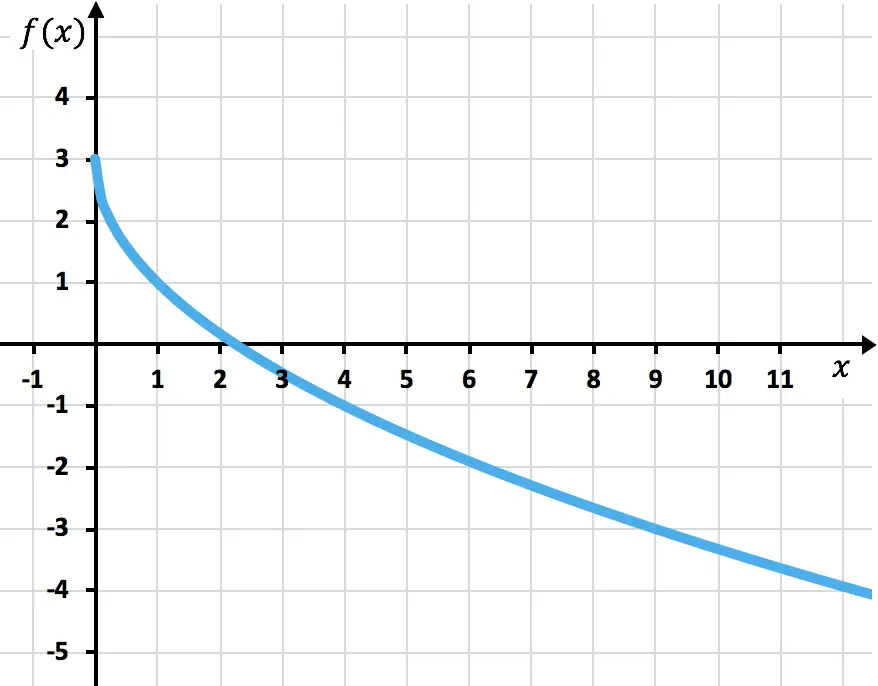
Ejercicio 5

Realiza la representación gráfica de la siguiente función irracional o radical:

$f(x)= \sqrt{-x+5}$

Ver solución

Antes de trazar la función, tenemos que calcular el dominio de la función:

$-x+5\ge 0$

$-x\ge -5$

$x\le\cfrac{-5}{-1}=5$

Recuerda que si en una inecuación cambiamos de lado un número negativo que está multiplicando o dividiendo también hay que cambiar el signo de la inecuación.

$x\le5$

$\text{Dom } f = (-\infty,5]$

Ahora construimos una tabla de valores evaluando la función en puntos que pertenecen al dominio de la función:

$x= 5 \ \longrightarrow \ f(5)=\sqrt{-5+5}=0$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{-4+5}=1$

$x= 1 \ \longrightarrow \ f(1)=\sqrt{-1+5}=2$

$x= -4 \ \longrightarrow \ f(-4)=\sqrt{-(-4)+5}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 5 & 0 \\ 4 & 1 \\ 1 & 2 \\ -4 & 3 \end{array}$

Y, para acabar, solo nos queda representar los puntos y pintar la función en el gráfico:

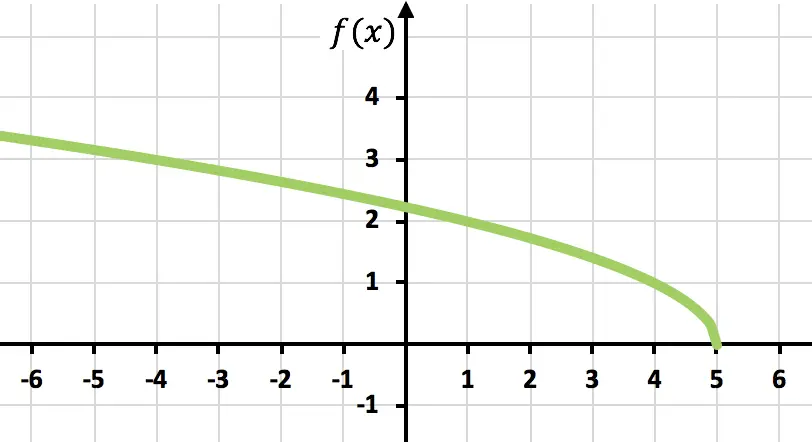
ejercicios resueltos de funciones radicales o irracionales

Ejercicio 6

Representa en una gráfica la siguiente función irracional o radical:

$f(x)= \sqrt{x^2-5x+4}$

Ver solución

Primero debemos calcular el dominio de la función:

$x^2-5x+4\ge 0$

En este caso hemos obtenido una inecuación de segundo grado, por lo que tenemos que aplicar la fórmula de las ecuaciones de segundo grado para resolverla:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle x=\cfrac{-(-5)\pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1} = \cfrac{5\pm 3}{2} =\begin{cases} 4 \\[2ex] 1 \end{cases}$

Dividimos la recta en tres trozos con las raíces obtenidas:

Y sustituimos un número de cada tramo en la inecuación, para ver qué tramos cumplen la inecuación y, en consecuencia, pertenecen al dominio:

$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 0}$ $0^2-5\cdot 0+4\ge 0 \ \longrightarrow \ 4\ge 0$ ✅

$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 2}$ $2^2-5\cdot 2+4\ge 0 \ \longrightarrow \ -10\ \cancel{\ge } \ 0$ ❌

$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 5}$ $5^2-5\cdot 5+4\ge 0 \ \longrightarrow \ 4\ge 0$ ✅

Por lo tanto, los tramos que cumplen con la inecuación son los de los lados:

De modo que el dominio de la función es:

$\text{Dom } f = (-\infty,1]\cup [4,+\infty)$

Una vez hemos calculado el dominio de la función, construimos una tabla de valores otorgando a la función valores de dentro del intervalo del dominio:

$x= 1 \ \longrightarrow \ f(1)=\sqrt{1^2-5\cdot 1+4} =0$

$x= 0 \ \longrightarrow \ f(0)=\sqrt{0^2-5\cdot 0+4} =2$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{(-1)^2-5\cdot (-1)+4} =3,16$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{4^2-5\cdot 4+4} =0$

$x= 5 \ \longrightarrow \ f(5)=\sqrt{5^2-5\cdot 5+4} =2$

$x= 6 \ \longrightarrow \ f(6)=\sqrt{6^2-5\cdot 6+4} =3,16$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 0 & 2 \\ -1 & 3,16 \\ 4 & 0 \\ 5 & 2 \\ 6 & 3,16 \\ \end{array}$

Finalmente, representamos los puntos obtenidos en la gráfica y trazamos la función:

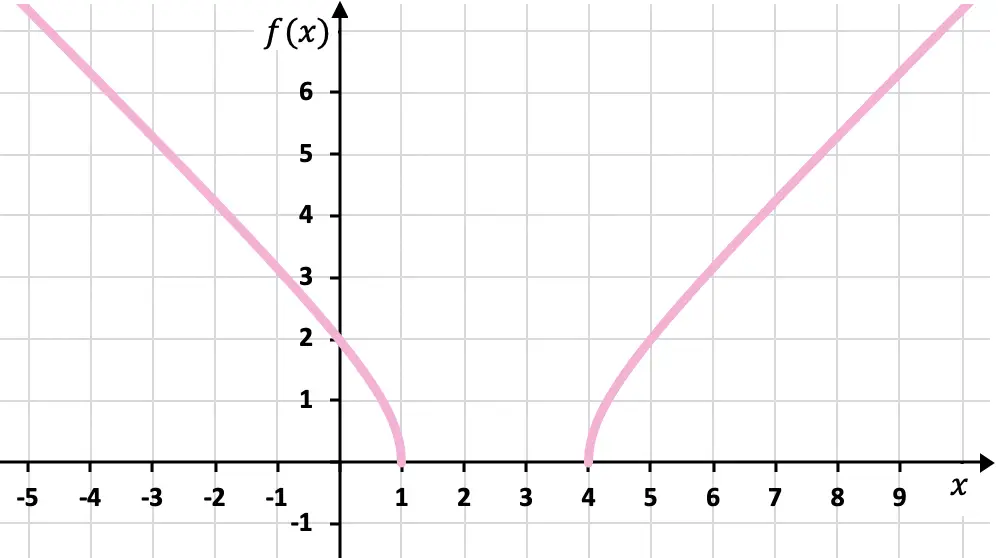
grafica de una funcion irracional o radical de indice par

Ejercicio 7

Representa en la gráfica la siguiente función formada por una raíz:

$f(x)= \sqrt[3]{x}$

Ver solución

Se trata de una función irracional cuya raíz es de índice impar, con lo que el dominio de la función son todos los números reales:

$\text{Dom } f = \mathbb{R}$

Por tanto podemos coger cualquier punto para crear la tabla de valores. En este caso buscaremos muchos puntos porque es una raíz cúbica:

$x= 0 \ \longrightarrow \ f(0)= \sqrt[3]{0} = 0$

$x= 0,5 \ \longrightarrow \ f(0,5)= \sqrt[3]{0,5} = 0,79$

$x= -0,5 \ \longrightarrow \ f(-0,5)= \sqrt[3]{-0,5} = -0,79$

$x= 1 \ \longrightarrow \ f(1)= \sqrt[3]{1} = 1$

$x= -1 \ \longrightarrow \ f(-1)= \sqrt[3]{-1} = -1$

$x= 8 \ \longrightarrow \ f(8)= \sqrt[3]{8} = 2$

$x= -8 \ \longrightarrow \ f(-8)= \sqrt[3]{-8} = -2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 0 \\ 0,5 & 0,79 \\ -0,5 & -0,79 \\ 1 & 1 \\ -1 & -1 \\ 8 & 2 \\ -8 & -2 \end{array}$

Finalmente, representamos los puntos encontrados y trazamos la función en la gráfica:

graficar una funcion irracional o radical de indice impar

Ejercicio 8

Resuelve el siguiente problema relacionado con las funciones irracionales (o radicales):

El consumo de una batería de un móvil viene dado por la siguiente función:

$f(t)=\sqrt{x-K \vphantom{(-K)}}$

Donde el consumo se expresa en miliamperios (mA) y $t$ es el tiempo transcurrido en minutos.

Determina el valor de la constante $K$ para que pasados 4 minutos el consumo sea de 35 mA.

Ver solución

Que pasados 4 minutos el consumo sea de 35 mA quiere decir que cuando t es 4, f(t) es 35. Por tanto f(4)=35.

$f(4)=\sqrt{4-K} = 35$

$\sqrt{4-K} = 35$

Así que ahora debemos resolver la ecuación que hemos obtenido. Si nos fijamos, se trata de una ecuación irracional ya que tiene una raíz. En este tipo de ecuaciones lo primero que debemos hacer es aislar la raíz en un lado, que en este caso ya está aislada. Una vez está aislada, debemos elevar al cuadrado los dos lados de la ecuación:

$\left( \sqrt{4-K} \right)^2= 35^2$