Función polinómica

Aquí encontrarás qué son las funciones polinómicas y cuáles son todos los tipos de funciones polinómicas. Además, también explicamos las propiedades de las funciones polinómicas.

¿Qué es una función polinómica?

Por lo tanto, una función polinómica se describe matemáticamente con la siguiente expresión:

Por otro lado, las funciones polinómicas también se pueden definir usando la siguiente fórmula:

Donde los términos y son el coeficiente y la variable respectivamente de cada monomio que forma la función polinómica.

El término , llamado término principal, indica el grado de la función polinómica, ya que es el monomio de mayor grado de la función. O dicho de otra forma, el exponente de valor más grande es el que indica el grado de la función polinómica.

Aunque más abajo veremos más características de las funciones polinómicas, el dominio de cualquier función polinómica son todos los números reales.

Tipos de funciones polinómicas

Vista la definición de función polinómica, vamos a ver ahora cuáles son todos los tipos de funciones polinómicas que existen.

Función constante

La función constante es una función polinómica de grado 0, por tanto, es un tipo de función que siempre toma la misma imagen para cualquier valor de la variable independiente (x).

La expresión general de la función constante es la siguiente:

Por ejemplo, las siguientes tres funciones son constantes o funciones polinómicas de grado cero:

La representación gráfica de una función constante es una recta horizontal (paralela al eje x) de valor igual a la constante.

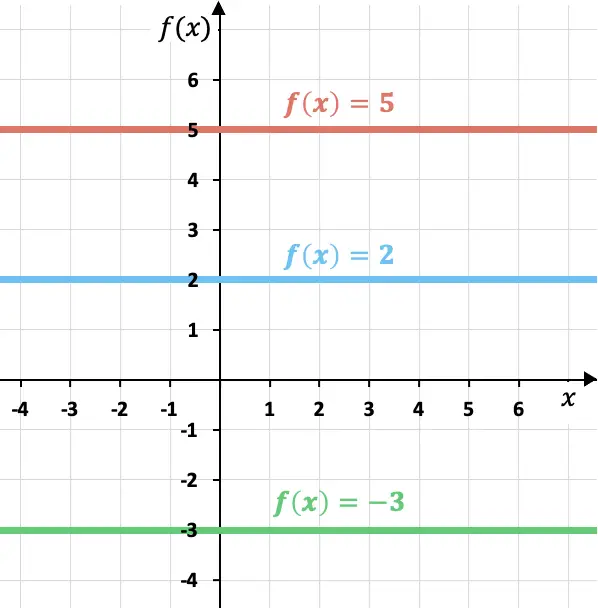
Puedes ver más características sobre este tipo de función en el siguiente enlace:

➤ Ver: características de la función constante

Función lineal

Una función lineal, también llamada función afín, es una función polinómica de primer grado. De manera que una función polinómica de este tipo solamente puede estar compuesta por un término lineal y un término independiente:

Donde  es la pendiente de la recta y  es la ordenada en el origen, es decir, donde la función corta con el eje Y.

Ejemplos de funciones lineales o funciones polinómicas de primer grado:

Hay quien distingue la función lineal de la función afín según si la función tiene el término o no, siendo la función afín con ordenada en el origen y la función lineal sin.

La representación gráfica de las funciones lineales siempre son rectas cuyo grado de inclinación depende del valor de la pendiente de la función.

A continuación puedes ver graficada la función polinómica de primer grado

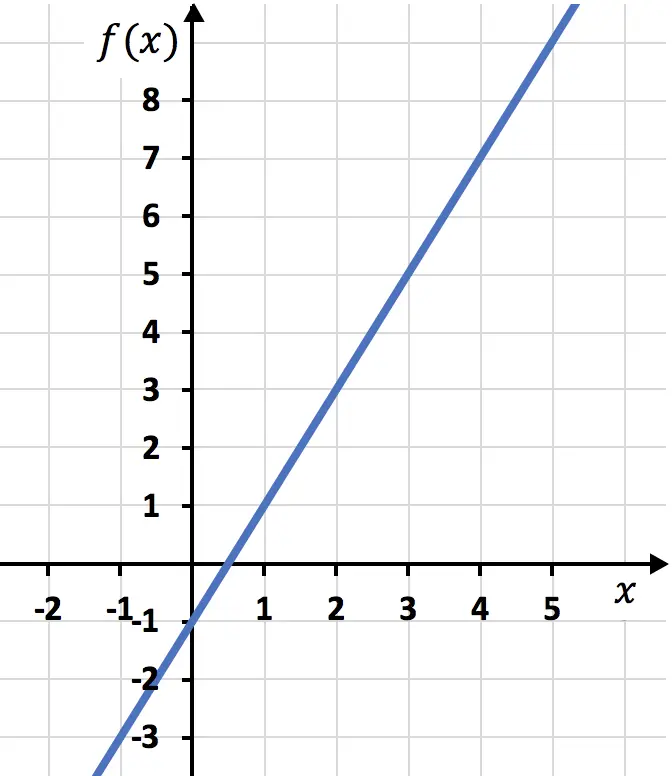
Sin embargo, para representar gráficamente una función lineal debes tener claro varios conceptos. En el siguiente enlace encontrarás la explicación paso a paso de cómo graficar una función polinómica de este tipo:

➤ Ver: cómo graficar una función lineal

Función cuadrática

Una función cuadrática es una función polinómica de grado 2, es decir, es una función en la que el término de mayor grado es de segundo grado.

Por lo tanto, la fórmula de una función cuadrática es la siguiente:

Donde es el término cuadrático, el término lineal y el término independiente de la función polinómica.

Ejemplos de funciones cuadráticas o funciones polinómicas de segundo grado:

La gráfica de una función cuadrática siempre es una parábola y su forma depende del signo del coeficiente principal

• Si el coeficiente es positivo, la función cuadrática es convexa (con forma de ).
• En cambio, si el coeficiente es negativo, la función cuadrática es cóncava (con forma de ).

Así pues, con el signo del coeficiente principal de la función polinómica de segundo grado podemos saber la forma que tendrá su gráfica, pero para hacer su representación gráfica exacta se debe seguir un procedimiento concreto. Puedes ver este procedimiento en el siguiente enlace:

➤ Ver: cómo graficar una función cuadrática

Función cúbica

Una función cúbica es una función polinómica de tercer grado. Por lo tanto, este tipo de funciones polinómicas se expresan algebraicamente de la siguiente manera:

Ejemplos de funciones cúbicas o funciones polinómicas de tercer grado:

Las representaciones gráficas de las funciones cúbicas corresponden a curvas cúbicas. Sin embargo, para representar este tipo de funciones en un gráfico se debe seguir un procedimiento complicado (incluye derivadas). Puedes consultar cómo se hace aquí:

➤ Ver: cómo representar una función

Com puedes ver, en realidad los tipos de funciones polinómicas son infinitos, ya que un polinomio puede tener infinitos términos. Así, por ejemplo, una función cuártica es como una función cúbica pero añadiendo un término de cuarto grado. Lo importante es que entiendas que el tipo de función polinómica lo marca el grado de la función.

Propiedades de las funciones polinómicas

Las funciones polinómicas tienen las siguientes características:

• El dominio de cualquier función polinómica es el conjunto de los números reales.

• Todas las funciones polinómicas son continuas.

• Las funciones polinómicas de grado mayor que 1 no tienen asíntotas.

• Independientemente del tipo de función polinómica que sea, el único punto de corte con el eje de las ordenadas (eje Y) está a la altura de su término independiente, es decir, en el siguiente punto:

• En cambio, una función polinómica intercepta el eje de las abscisas (eje X), a lo sumo, tantas veces como el grado de la función.

• Si una función polinómica solo tiene términos de grado par, implica que es simétrica respecto al eje OY. Por otro lado, si una función polinómica solo tiene términos de grado impar, significa que la función es simétrica respecto al origen de coordenadas.

• El número de extremos relativos (máximos o mínimos) de una función polinómica es, como mucho, el grado del polinomio de la función menos 1.

• El número de puntos de inflexión de una función polinómica es, como máximo, igual al grado del polinomio de la función menos 2.

• Se pueden hacer operaciones con funciones polinómicas:
  • La suma de dos funciones polinómicas da como resultado otra función polinómica.
  • El producto de dos funciones polinómicas da lugar a otra función polinómica.
  • Al multiplicar una función polinómica por un escalar (número real) se obtiene una función polinómica similar pero con su gráfica contraída o expandida.
  • La composición de dos funciones polinómicas es igual a otra función polinómica.