Función cuadrática o parábola

En esta página se explica qué es una función cuadrática junto con todas sus características: curvatura, vértice, puntos de corte con los ejes, etc. También encontrarás cómo se representa una función cuadrática en una gráfica. Y, finalmente, podrás practicar con los ejemplos, ejercicios resueltos paso a paso y problemas que hay sobre las funciones cuadráticas.

¿Qué es una función cuadrática?

La definición de función cuadrática es la siguiente:

En matemáticas, una función cuadrática (o parabólica) es una función polinómica de grado 2, es decir, una función en la que el término de mayor grado es de segundo grado. Por lo tanto, la fórmula de una función cuadrática es la siguiente:

f(x)=ax^2+bx+c

Donde:

  • ax^2 es el término cuadrático.
  • bx es el término lineal.
  • c es el término independiente.

El dominio de una función cuadrática siempre son todos los números reales.

\text{Dom } f=\mathbff{R}

Concavidad y convexidad de una función cuadrática

Analizar la curvatura de una función cuadrática o parábola es muy simple, porque solo depende del coeficiente de segundo grado.

  • Si el coeficiente a es positivo, la función cuadrática es convexa (con forma de \bm{\cup}). En consecuencia, el vértice es un mínimo.
  • Si el coeficiente a es negativo, la función cuadrática es cóncava (con forma de \bm{\cap}). Por lo que el vértice es un máximo.
funcion cuadratica o parabola convexa
funcion cuadratica o parabola concava

Nota: La comunidad matemática aún no está totalmente de acuerdo y, por tanto, hay profesores que lo dicen al revés: llaman función cóncava la que tiene forma de \bm{\cup}, y función convexa la que tiene forma de \bm{\cap}. En cualquier caso, lo importante es saber qué forma tiene la función, independientemente del nombre.

Vértice de una función cuadrática

Para poder graficar una función cuadrática es necesario saber las coordenadas del vértice de la parábola.

Para hallar el vértice de una función cuadrática tenemos que calcular la coordenada X del punto mediante la siguiente fórmula:

\displaystyle x=\frac{-b}{2a}

Luego podemos hallar la otra coordenada del vértice calculando la imagen de la función en ese punto:

\displaystyle f\left(\frac{-b}{2a}\right)

De modo que las coordenadas del vértice de una función cuadrática (o parábola) son:

\displaystyle \left(\frac{-b}{2a} \ , \ f\left(\frac{-b}{2a}\right)\right)

Puntos de corte con los ejes de una función cuadrática

Una parábola siempre corta con el eje de ordenadas (eje Y), y esto sucede cuando x=0. Por lo tanto, para calcular el punto de corte de una función cuadrática con el eje Y se debe resolver f(0).

Por ejemplo, el punto de corte con el eje OY de la siguiente función cuadrática es:

f(x)=x^2-2x+1

f(0)=0^2-2\cdot 0+1 = 1

\bm{(0,1)}

Por otro lado, el punto de corte de una función cuadrática con el eje de abscisas (eje X) se produce cuando f(x)=0. Así que para calcular el punto de corte con el eje X hay que resolver la ecuación f(x)=0.

A modo de ejemplo, a continuación tienes el cálculo del punto de corte con el eje OX de la misma función cuadrática:

f(x)=x^2-2x+1

0=x^2-2x+1

Resolvemos la ecuación de segundo grado con la fórmula general:

x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}

x=\cfrac{-(-2)\pm \sqrt{(-2)^2-4\cdot 1\cdot1}}{2\cdot 1} =\cfrac{2\pm 0}{2} = 1

De modo que el punto de corte de la función cuadrática con el eje X es:

\bm{(1,0)}

En este caso hemos obtenido una única solución de la ecuación de segundo grado, sin embargo, podríamos haber obtenido dos soluciones. En tal caso, significa que la función cuadrática corta el eje X en dos puntos distintos.

Ejemplo de cómo representar una función cuadrática o parábola

Vamos a ver cómo representar una función de segundo grado en un gráfico mediante un ejemplo.

  • Representa gráficamente la siguiente función:

f(x)=x^2-4x+5

Lo primero que debemos hacer es calcular el vértice de la parábola. Para ello, utilizamos la fórmula que hemos visto más arriba:

x = \cfrac{-b}{2a} = \cfrac{-(-4)}{2\cdot 1}= \cfrac{4}{2}= 2

Una vez sabemos dónde estará el vértice, debemos construir una tabla de valores: calculamos el valor de la función en el vértice y en los puntos de su alrededor:

f(x)=x^2-4x+5

  • x= 2 \ \longrightarrow \ f(2) = 2^2-4\cdot2+5=1
  • x= 1 \ \longrightarrow \ f(1)=1^2-4\cdot1+5=2
  • x= 3 \ \longrightarrow \ f(3) = 3^2-4\cdot3+5=2
  • x= 0 \ \longrightarrow \ f(0) = 0^2-4\cdot0+5=5
  • x= 4 \ \longrightarrow \ f(4) = 4^2-4\cdot4+5=5

\begin{array}{c|c} x & f(x) \\ \hline 2 & 1 \\ 1 & 2 \\ 3 & 2 \\ 0 & 5 \\ 4 & 5 \end{array}

También se pueden calcular los puntos de corte de la función cuadrática con los ejes cartesianos para dibujar mejor la parábola, pero no es estrictamente necesario.

Ahora representamos los puntos obtenidos en una gráfica:

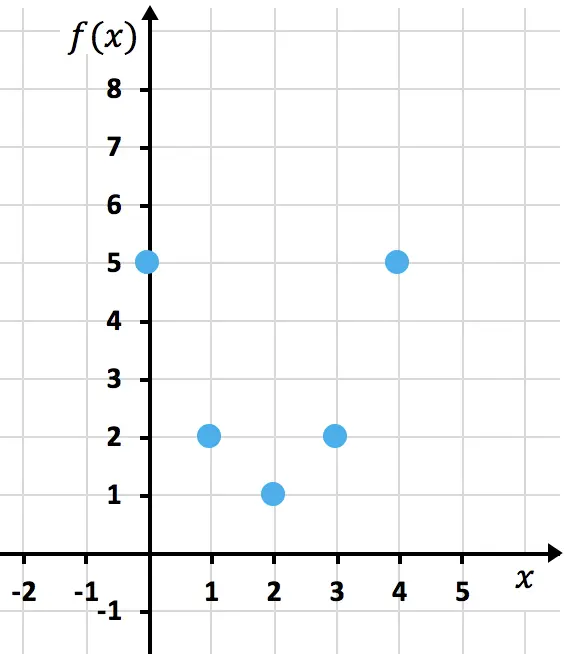
ejemplo de como representar una funcion cuadratica o parabola

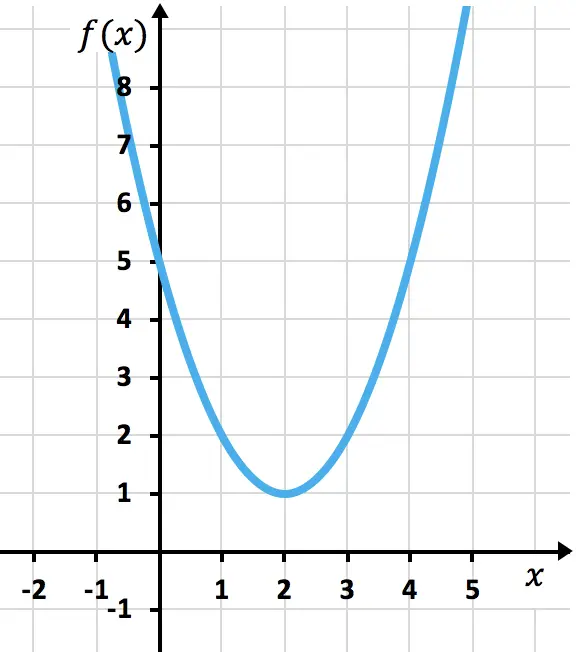
Y finalmente, unimos los puntos formando la parábola. Luego alargamos las ramas de la parábola para indicar que sigue hacia arriba:

representacion de una funcion cuadratica o parabola

Ejercicios resueltos de funciones cuadráticas

Ejercicio 1

Halla el vértice de la siguiente función cuadrática:

f(x)=2x^2+8x+4

Primero calculamos la coordenada X del vértice mediante la fórmula:

x = \cfrac{-b}{2a} = \cfrac{-8}{2\cdot 2} = \cfrac{-8}{4} = -2

Y ahora calculamos la otra coordenada evaluando la función en el punto:

\begin{aligned} f(-2) & =2(-2)^2+8(-2)+4 \\[1.7ex] & = 2 \cdot 4 - 16 +4 \\[1.7ex] & = 8-16+4 \\[1.7ex] & = -4 \end{aligned}

De manera que el vértice de la función cuadrática es:

\bm{(-2,-4)}

 

Ejercicio 2

Encuentra los puntos de corte de la siguiente función con los ejes:

f(x)=x^2-4x+3

Para calcular el punto de corte con el eje Y debemos calcular f(0):

f(0)=0^2-4\cdot 0+3 = 3

Así que la función pasa por el eje Y en el punto:

\bm{(0,3)}

Y para hallar los puntos de corte con el eje X debemos resolver f(x)=0:

f(x)=x^2-4x+3

0=x^2-4x+3

Calculamos las raíces de la ecuación de segundo grado con la fórmula:

x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}

\displaystyle x=\cfrac{-(-4)\pm \sqrt{(-4)^2-4\cdot 1\cdot 3}}{2\cdot 1} =\cfrac{4\pm 2}{2} = \begin{cases} 3 \\[2ex] 1 \end{cases}

De manera que la función corta con el eje X en dos puntos:

\bm{(1,0) \qquad (3,0)}

 

Ejercicio 3

Representa gráficamente la siguiente función cuadrática:

f(x)=-x^2+4x+1

Se trata de una función cuadrática. Por tanto, para representarla primero debemos calcular la coordenada X del vértice de la parábola con la fórmula:

x = \cfrac{-b}{2a} = \cfrac{-4}{2\cdot (-1)} = \cfrac{-4}{-2} = 2

Ahora creamos la tabla de valores. Para ello calculamos el valor de f(x) en el vértice y alrededor del vértice:

x= 2 \ \longrightarrow \ f(2)=-2^2+4\cdot2+1 = 5

x= 1 \ \longrightarrow \ f(1)=-1^2+4\cdot1+1 = 4

x= 3 \ \longrightarrow \ f(3)=-3^2+4\cdot3+1 =4

x= 0 \ \longrightarrow \ f(0)=-0^2+4\cdot0+1 = 1

x= 4 \ \longrightarrow \ f(4)=-4^2+4\cdot4+1 = 1

\begin{array}{c|c} x & f(x) \\ \hline 2 & 5 \\ 1 & 4 \\ 3 & 4 \\ 0 & 1 \\ 4 & 1 \end{array}

Y, por último, representamos los puntos en el gráfico y trazamos la parábola:

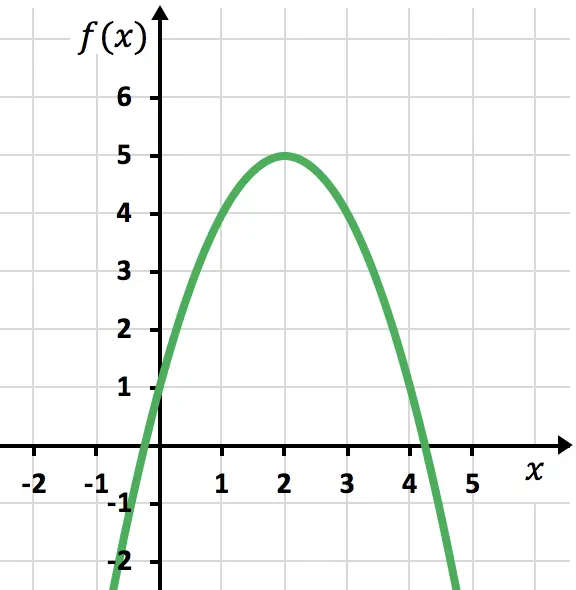
ejemplo de funcion cuadratica

 

Ejercicio 4

Realiza la representación gráfica de la siguiente función cuadrática:

f(x)=-2x^2-8x-1

Se trata de una función de segundo orden. Por tanto, para representarla primero debemos hallar la coordenada X del vértice de la parábola con la fórmula:

x = \cfrac{-b}{2a} = \cfrac{-(-8)}{2\cdot (-2)} = \cfrac{+8}{-4} = -2

Ahora construimos la tabla de valores. Para ello calculamos el valor de f(x) en el vértice y alrededor del vértice:

x= -2 \ \longrightarrow \ f(-2)=-2(-2)^2-8\cdot(-2)-1 =7

x= -1 \ \longrightarrow \ f(-1)=-2(-1)^2-8\cdot(-1)-1= 5

x= -3 \ \longrightarrow \ f(-3)=-2(-3)^2-8\cdot(-3)-1= 5

x= 0 \ \longrightarrow \ f(0)=-2\cdot0^2-8\cdot0-1= -1

x= -4 \ \longrightarrow \ f(-4)=-2(-4)^2-8\cdot(-4)-1= -1

\begin{array}{c|c} x & f(x) \\ \hline -2 & 7 \\ -1 & 5 \\ -3 & 5 \\ 0 & -1 \\ -4 & -1 \end{array}

Finalmente, representamos los puntos en la gráfica y trazamos la parábola:

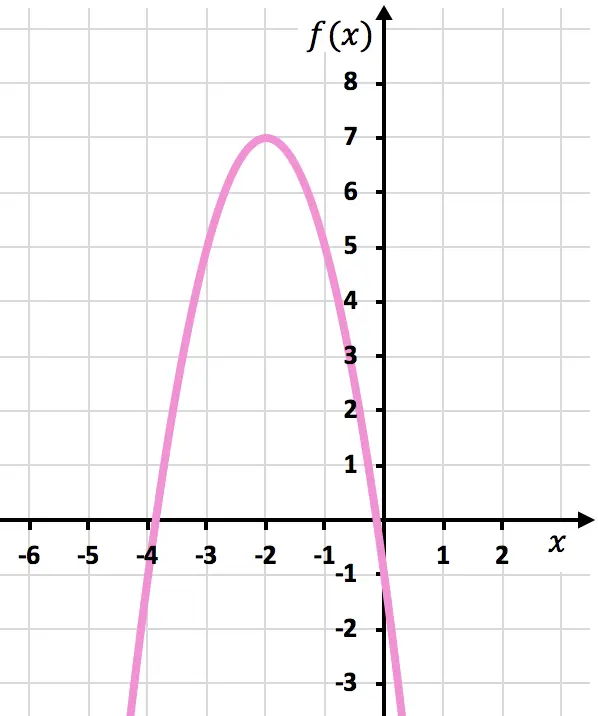
ejercicio resuelto paso a paso de funcion cuadratica

 

Ejercicio 5

Representa en una gráfica la siguiente función cuadrática incompleta:

f(x)=x^2+2

Es una función polinómica de grado dos. Por tanto, para representarla primero debemos calcular la coordenada X del vértice de la parábola con la fórmula:

x = \cfrac{-b}{2a} = \cfrac{-0}{2\cdot1} = \cfrac{0}{2} = 0

En este caso la función es incompleta, ya que no tiene término de primer grado. Por eso b=0 .

Ahora hacemos la tabla de valores. Para ello calculamos el valor de f(x) en el vértice y alrededor del vértice:

x= 0 \ \longrightarrow \ f(0)=0^2+2=2

x= 1 \ \longrightarrow \ f(1)=1^2+2=3

x= -1 \ \longrightarrow \ f(-1)=(-1)^2+2=3

x= 2 \ \longrightarrow \ f(2)=2^2+2=6

x= -2 \ \longrightarrow \ f(-2)=(-2)^2+2=6

\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 3 \\ -1 & 3 \\ 2 & 6 \\ -2 & 6 \end{array}

Por último, representamos los puntos en el gráfico y dibujamos la parábola:

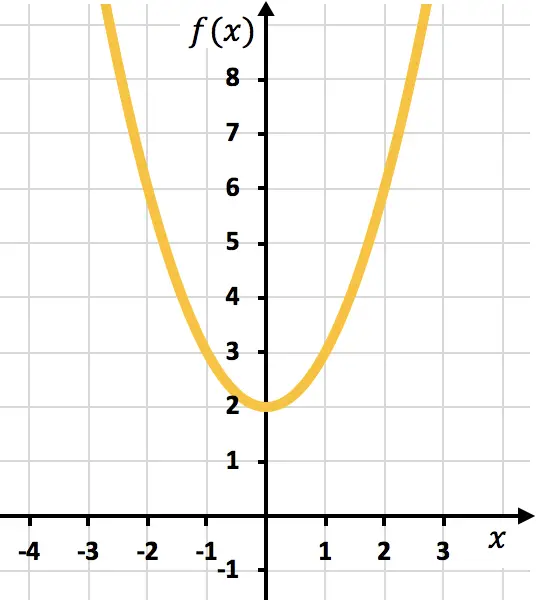
ejercicios resueltos de representar una funcion cuadratica incompleta

 

Ejercicio 6

Resuelve el siguiente problema relacionado con las funciones cuadráticas:

El coste de producción de un producto viene definido por la siguiente función:

f(x)=x^2-12x+76

Donde x son las unidades producidas (en millares) y f(x) es el coste de producir las unidades (en millares de €).

  • Representa la función del coste de producción en un gráfico.
  • Determina cuántos millares de unidades se tienen que producir para minimizar los costes.

Se trata de una función cuadrática. Por tanto, para representarla primero debemos encontrar la coordenada X del vértice de la parábola con la fórmula:

x = \cfrac{-b}{2a} = \cfrac{-(-12)}{2\cdot 1} = \cfrac{12}{2} = 6

Ahora hacemos la tabla de valores. Para ello calculamos el valor de f(x) en el vértice y alrededor del vértice:

x= 6 \ \longrightarrow \ f(6)=6^2-12\cdot6+76 = 40

x= 5 \ \longrightarrow \ f(5)=5^2-12\cdot5+76 = 41

x= 7 \ \longrightarrow \ f(7)=7^2-12\cdot7+76 = 41

x= 4 \ \longrightarrow \ f(4)=4^2-12\cdot4+76 = 44

x= 8 \ \longrightarrow \ f(8)=8^2-12\cdot8+76 = 44

\begin{array}{c|c} x & f(x) \\ \hline 6 & 40 \\ 5 & 41 \\ 7 & 41 \\ 4 & 44 \\ 8 & 44 \end{array}

Ahora representamos los puntos en el gráfico y trazamos la parábola:

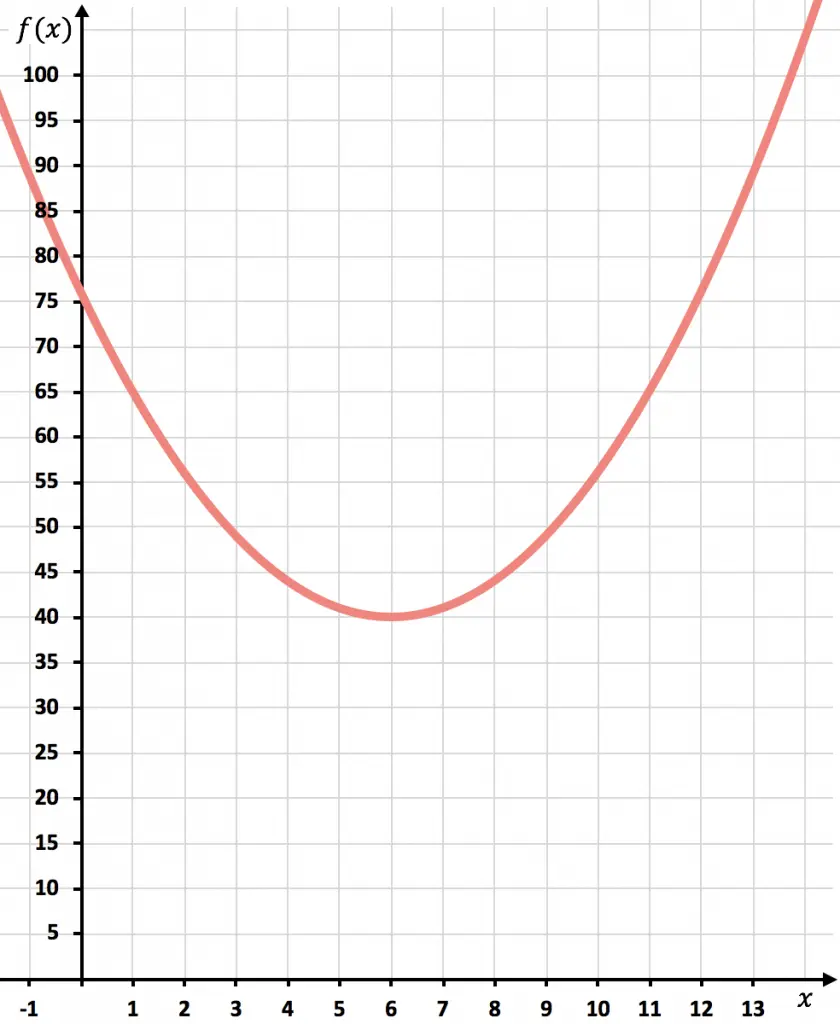
problema de funcion cuadratica o parabola

Una vez representada la función, vamos a ver en qué punto se minimizan los costes.

Tal y como se ve en el gráfico, los costes mínimos se conseguirán en el vértice de la parábola. Porque es donde la función toma el valor más pequeño.

En conclusión, se minimizarán los costes produciendo 6 millares de unidades.

 

Ejercicio 7

Resuelve el siguiente problema de funciones cuadráticas:

Un atleta realiza un lanzamiento de jabalina cuya trayectoria se puede representar con la siguiente función:

h(x) = -0,025x^2+2x+2

Donde x son los metros recorridos por la jabalina y h su altura (también en metros).

¿Cuál es la máxima altura a la que consigue llegar la jabalina?

Se trata de una función cuadrática, por lo tanto, la trayectoria de la jabalina será una parábola.

Además como el coeficiente del término cuadrático es negativo (-0,025), la parábola tendrá forma de U invertida y sus ramas irán hacia abajo. Así que la jabalina alcanzará la altura máxima en el vértice, ya que será el punto más alto de la parábola.

De modo que calculamos la coordenada X del vértice de la parábola con la fórmula:

x = \cfrac{-b}{2a} = \cfrac{-2}{2\cdot (-0,025)} = \cfrac{-2}{-0,05} = 40

Y luego calculamos la altura a la que estará la jabalina en ese punto evaluando la función en x=40:

h(40) = -0,025\cdot (40)^2+2\cdot 40+2 = 42

De manera que la altura máxima a la que consigue llegar la jabalina es 42 metros.

 

Ejercicio 8

Resuelve el siguiente problema sobre las funciones cuadráticas:

Los costes de producción (en euros) de una empresa vienen definidos por la siguiente función:

C(q)=40000+20q+q^2

Donde q son las unidades producidas.

Y el precio de venda de cada unidad es de 520 €.

  • ¿Qué beneficio conseguirá la empresa si vende 150 unidades?
  • ¿Cuántas unidades se deben vender para que el beneficio sea máximo?

La empresa ingresa 520 € por cada unidad que vende. Por tanto, la función que define los ingresos es:

I(q)=520\cdot q = 520q

Donde q son las unidades vendidas.

Pero nos preguntan por el beneficio, que son los ingresos menos los costes. Así que restamos los ingresos menos los costes para obtener la función que describe el beneficio de la empresa:

B(q)=I(q)-C(q)

B(q)=520q - (40000+20q+q^2)

B(q)=520q - 40000-20q-q^2

B(q)=-q^2 + 500q - 40000

Una vez sabemos la función que describe el beneficio de la empresa, solamente tenemos que sustituir 150 en la expresión de la función para calcular el beneficio que obtendrá la empresa vendiendo 150 unidades:

\begin{aligned} B(150) & =-(150)^2 + 500\cdot 150 - 40000 \\[2ex] & = -22500+75000 - 40000 \\[2ex] & = \bm{12500} \end{aligned}

De modo que vendiendo 150 unidades la empresa conseguirá 12500 € de beneficio.

El enunciado también nos pide calcular con cuántas unidades se consigue el máximo beneficio.

La función que describe el beneficio es una función cuadrática, con lo que tendrá forma de parábola. Y como el coeficiente del término de segundo grado es negativo (-1), la parábola tendrá forma de U invertida y sus ramas irán hacia abajo. Por tanto, los beneficios máximos se conseguirán en el vértice, ya que es el punto más alto de la parábola.

Así que calculamos la coordenada X del vértice de la parábola con la fórmula:

x = \cfrac{-b}{2a} = \cfrac{-500}{2\cdot(-1)} = \cfrac{-500}{-2} = 250

De modo que la empresa conseguirá el máximo beneficio vendiendo 250 unidades.

Por otro lado, aunque no lo pedía el enunciado, podemos determinar el beneficio que se conseguirá vendiendo estas 250 unidades:

B(250) =-(250)^2 + 500\cdot250- 40000= 22500 €

 

2 comentarios en “Función cuadrática o parábola”

    1. Funciones

      Hola Felip,

      Una parábola tiene tres incógnitas, que son los tres coeficientes del polinomio cuadrático:
      f(x)=ax^2+bx+c

      Si sabemos que el vértice de la parábola está en x=0, podemos relacionar los coeficientes a y b mediante la fórmula del vértice de una parábola:
      x=\cfrac{-b}{2a} \ \longrightarrow \ 0 = \cfrac{-b}{2a} \ \longrightarrow \ b=0

      Luego podemos obtener el coeficiente c sustituyendo las coordenadas del punto de corte con el eje Y en la ecuación:
      f(0)=a\cdot 0^2+c=20 \ \longrightarrow \ c=20

      Finalmente, encontramos el coeficiente a sustituyendo las coordenadas del punto de corte con el eje X en la ecuación:
      f(-20)=0 \ \longrightarrow \ a\cdot (-20)^2+20=0 \ \longrightarrow \ a=-0,05

      En conclusión, la ecuación de la parábola que nos pedía el problema es:
      f(x)=-0,05x^2+20

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *