Función lineal y función afín

En este post encontrarás la explicación de la función afín y de la función lineal, junto a las diferencias que existen entre estos dos tipos de funciones. Además, verás ejemplos de cómo representar en una gráfica tanto una función afín como una función lineal y cómo calcular sus expresiones a partir de dos puntos. Por último, podrás practicar con varios ejercicios resueltos paso a paso.

¿Qué es una función afín y una función lineal?

Las definiciones de función afín y función lineal son las siguientes:

Una función afín es una función polinómica de primer grado, es decir, es una función que representada en la gráfica es una línea recta. Las funciones afines son de la siguiente forma:

f(x)=mx+n

Donde m es la pendiente de la recta y n es la ordenada en el origen, es decir, donde la función corta con el eje vertical.

En matemáticas, las funciones afines también son conocidas como transformaciones lineales en el contexto del álgebra lineal.

Una función lineal es una función afín que no tiene término independiente. Por lo tanto, la fórmula de las funciones lineales es la siguiente:

f(x)=mx

Donde m es la pendiente de la recta.

El dominio y el recorrido (o rango) tanto de la función lineal como de la función afín son todos los números reales:

\text{Dom } f=\mathbff{R}

\text{Im } f= \mathbb{R}

¿Cuál es la diferencia entre una función lineal y una función afín?

Ahora que has visto los conceptos de función lineal y función afín, habrás notado que son muy similares entre sí. Sin embargo, la siguiente diferencia entre ellas es muy importante:

La única diferencia entre la función lineal y la afín es que la función lineal no tiene término independiente mientras que la función afín siempre tiene el coeficiente de la ordenada en el origen (n) diferente de cero (0).

Función lineal
f(x)=mx

Función afín
f(x)=mx+n

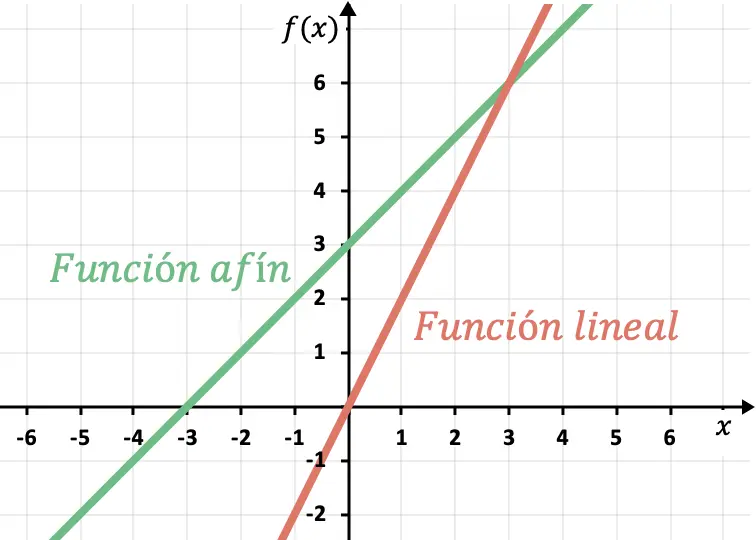
Esto implica que una función lineal siempre pasa por el origen de coordenadas, el punto (0,0). En cambio, una función afín nunca pasará por este punto porque tiene una ordenada en el origen distinta de 0.

cual es la diferencia entre una funcion lineal y una funcion afin

Pendiente y ordenada en el origen de una función lineal o afín

En este apartado vamos a analizar un ejemplo de una función afín o lineal para entender el significado de los términos m y n, o dicho de otra forma, la pendiente y la ordenada en el origen.

  • Determina la expresión de la función representada en el gráfico y clasifícala en función lineal o afín.

Este tipo de funciones siguen la siguiente expresión:

f(x)=mx+n

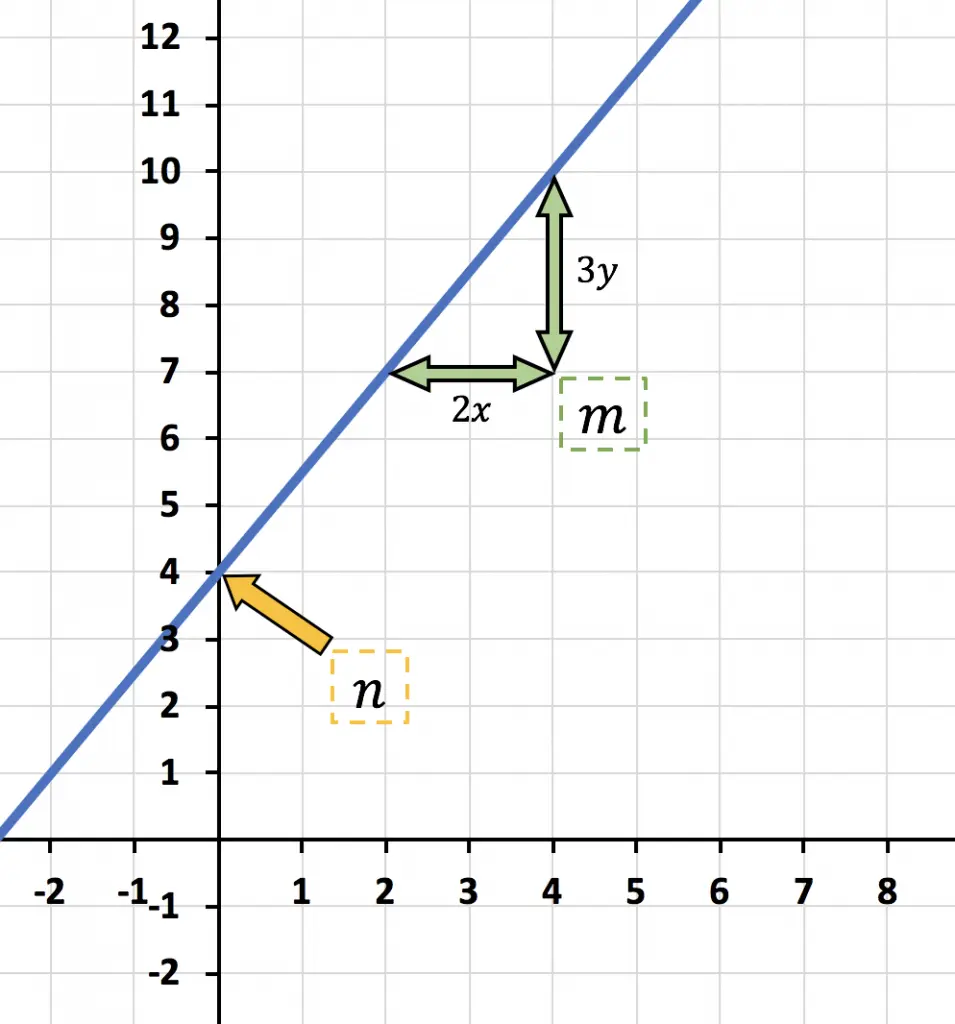
significado pendiente y ordenada en el origen funcion lineal o afin m y n

n es la ordenada en la origen, es decir, donde la función corta con el eje vertical Y. Por tanto en este caso:

n=4

Por otro lado, m es la pendiente de la recta. Y se puede calcular dividiendo la diferencia de y entre dos puntos entre la diferencia de x entre esos dos mismos puntos:

m=\cfrac{\Delta y }{\Delta x} = \cfrac{3}{2}

m indica «cuántas y sube por cada x», por tanto, en este caso la función «sube 3y por cada 2x».

En conclusión, la expresión de la función afín representada en el gráfico es:

\displaystyle \bm{f(x)=}\frac{\bm{3}}{\bm{2}}\bm{x+4}

Además, como la ordenada en el origen es diferente de cero, se trata de una función afín.

A continuación te mostramos más ejemplos de funciones lineales y afines para acabarlo de comprender:

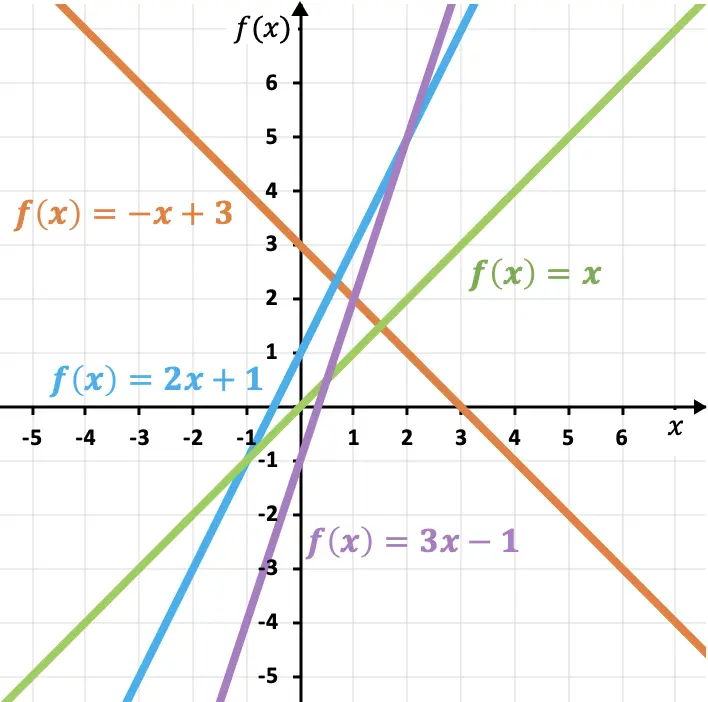
ejemplos de funciones lineales y afines

Como puedes observar en estos ejemplos, cuanto mayor es la pendiente más inclinada está la recta y, en consecuencia, más crece la función. Asimismo, el coeficiente de la pendiente determina el crecimiento o decrecimiento de una función:

  • Si la pendiente es positiva la función es creciente, es decir, crece a medida que aumenta la x.
  • Si la pendiente es negativa la función es decreciente, es decir, decrece a medida que aumenta la x.

Además, también se puede saber si dos rectas son paralelas o perpendiculares gracias a sus pendientes:

  • Cuando dos rectas tienen la misma pendiente son paralelas, es decir, no se cortan en ningún punto o son totalmente idénticas.

m_1 = m_2

  • Por contra, dos rectas son perpendiculares, es decir se cortan formando ángulo reto (90º), si sus pendientes cumplen la siguiente relación:

m_1 = -\cfrac{1}{m_2}

Ejemplo de cómo representar una función afín o lineal

Vamos a ver cómo representar una función de primer grado gráficamente mediante un ejemplo.

  • Representa en una gráfica la siguiente función afín:

f(x)=2x-1

Lo primero que debemos hacer es crear una tabla de valores. Para ello vamos otorgando los valores que queramos a x para obtener valores de f(x):

f(x)=2x-1

  • x= 0 \ \longrightarrow \ f(0) = 2\cdot0-1=-1
  • x= 1 \ \longrightarrow \ f(1) = 2\cdot1-1=1
  • x= 2 \ \longrightarrow \ f(2) = 2\cdot2-1=3
  • x= 3 \ \longrightarrow \ f(3) = 2\cdot3-1=5
  • x= 4 \ \longrightarrow \ f(4) = 2\cdot4-1=7

\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}

Aunque con una tabla de valores con dos puntos es suficiente, podemos hacer más puntos para asegurarnos de que está bien.

Una vez hemos creado la tabla de valores, representamos los puntos en el gráfico:

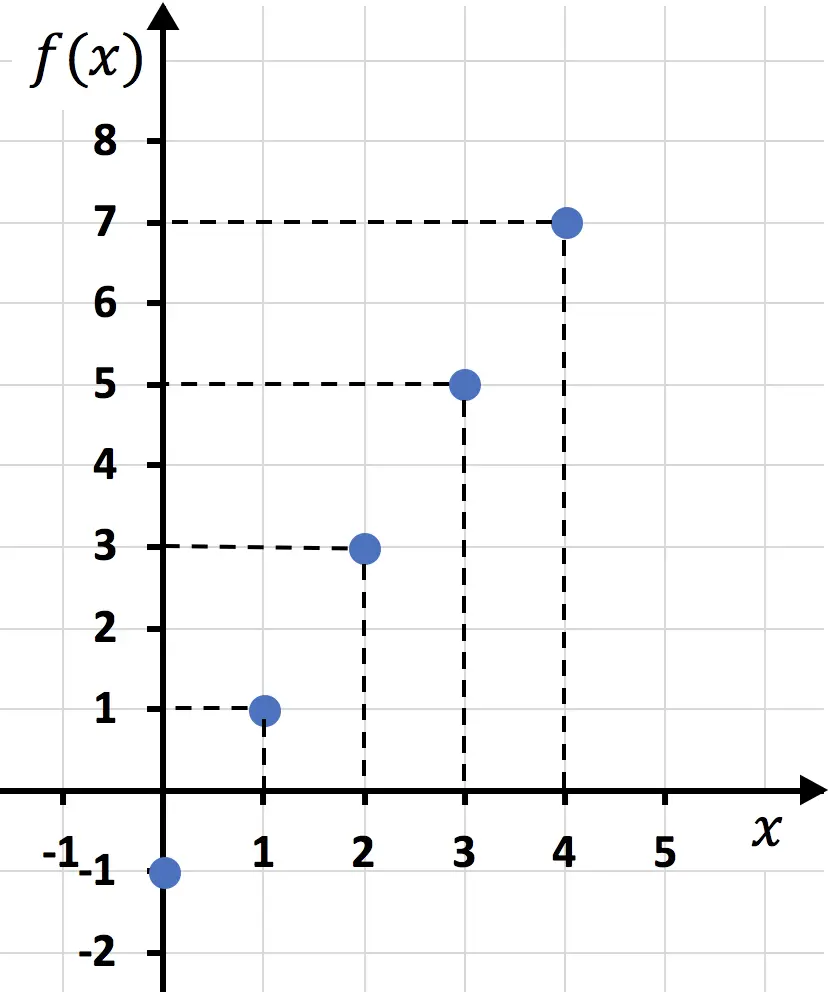
como representar una recta o funcion lineal o y afin

Y, finalmente, unimos los puntos y trazamos una recta:

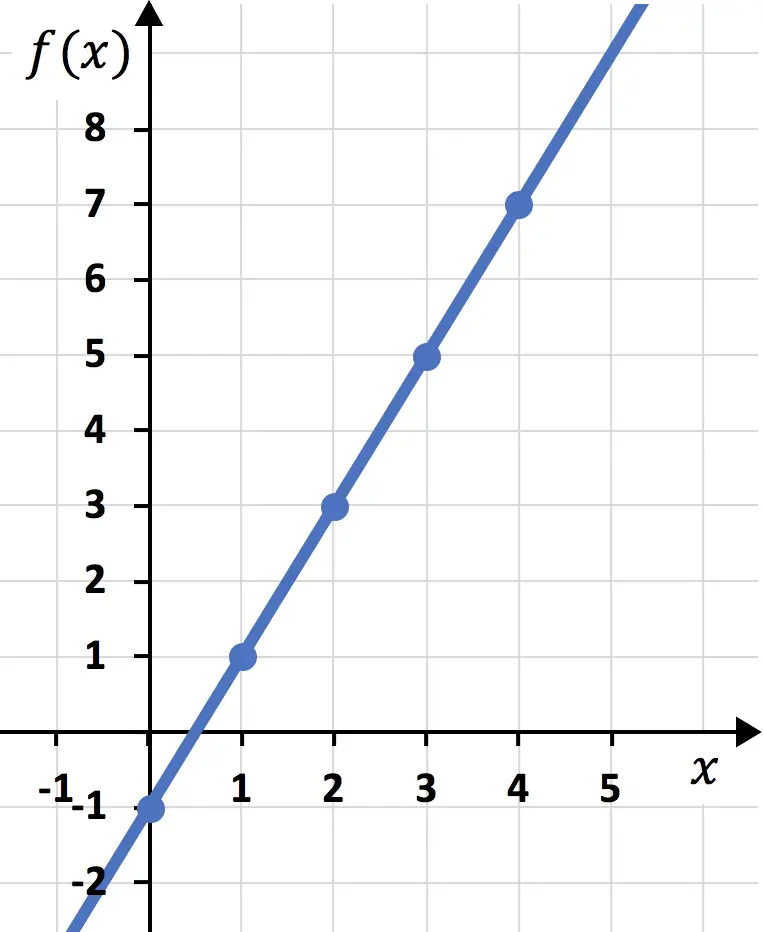
representacion grafica de una funcion lineal o afin

Y de esta manera ya hemos representado la función en un gráfico. Como ves no es complicado, simplemente hay que hacer primero una tabla de valores y luego dibujar los puntos en un gráfico.

Cómo calcular una función lineal o afín a partir de dos puntos

Veamos ahora cómo hallar una función de lineal o afín a partir de dos puntos mediante un ejemplo:

  • Calcula la función lineal que cumple f(3)=5 y pasa por el punto (1,-1).

Primero de todo, f(3)=5 quiere decir que la función pasa por el punto (3,5).

Por tanto, como tenemos dos puntos por los que pasa la función, podemos calcular la pendiente m de la función:

Dados dos puntos, P_1=(x_1,y_1) y P_2=(x_2,y_2), la pendiente m de la función se calcula:

m=\cfrac{y_2-y_1}{x_2-x_1}

En nuestro caso la función pasa por los puntos (3,5) y (1,-1). De modo que la pendiente m de la función es:

m=\cfrac{y_2-y_1}{x_2-x_1}=\cfrac{-1-5}{1-3} = \cfrac{-6}{-2} = 3

Así que la función será de la forma:

f(x) = mx+n \ \xrightarrow{m \ = \ 3} \ f(x)=3x+n

Una vez sabemos m podemos resolver la incógnita n. Para ello sustituimos en la ecuación las coordenadas de un punto que pertenezca a la función. Por ejemplo el punto (3,5):

f(x) = 3x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ 5} \ 5=3\cdot 3+n

Resolvemos la ecuación resultante:

5=3\cdot 3+n

5= 9 + n

5-9=n

-4=n

De manera que la función lineal es:

\bm{f(x)=3x-4}

Ejercicios resueltos de funciones lineales y afines

Ejercicio 1

Determina la pendiente y la ordenada en el origen de la siguiente función afín:

f(x)=-5x-2

Una función lineal es de la forma f(x)=mx+n .

Por tanto la pendiente de la función es el número que acompaña x, que en este caso es -5:

\bm{m=-5}

Y la ordenada en el origen es el término independiente, que en este caso es -2:

\bm{n=-2}

 

Ejercicio 2

Representa la siguiente función afín en un gráfico:

f(x)=x+1

Primero damos valores a x para crear la tabla de valores:

x= 0 \ \longrightarrow \ f(0)=0+1 = 1

x= 1 \ \longrightarrow \ f(1)=1+1= 2

x= 2 \ \longrightarrow \ f(2)=2+1 = 3

x= 3 \ \longrightarrow \ f(3)=3+1 = 4

x= 4 \ \longrightarrow \ f(4)=4+1 = 5

\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \\ 3 & 4 \\ 4 & 5 \end{array}

Y luego representamos los puntos de la tabla de valores en la gráfica y trazamos la recta:

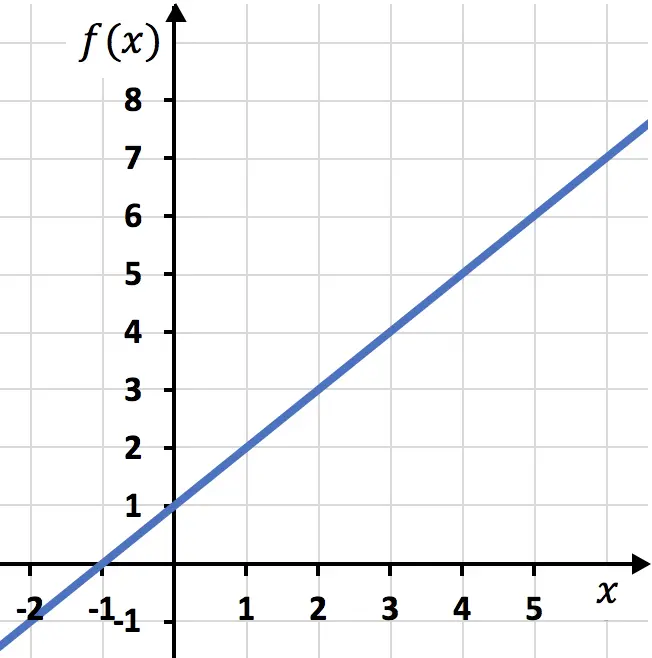
ejemplo de funcion lineal o afin

 

Ejercicio 3

Dibuja la siguiente función afín en la gráfica:

f(x)=-2x+6

Primero damos valores a x para crear la tabla de valores:

x= 0 \ \longrightarrow \ f(0)=-2\cdot0+6=6

x= 1 \ \longrightarrow \ f(1)=-2\cdot1+6=4

x= 2 \ \longrightarrow \ f(2)=-2\cdot2+6=2

x= 3 \ \longrightarrow \ f(3)=-2\cdot3+6=0

x= 4 \ \longrightarrow \ f(4)=-2\cdot4+6=-2

\begin{array}{c|c} x & f(x) \\ \hline 0 & 6 \\ 1 & 4 \\ 2 & 2 \\ 3 & 0 \\ 4 & -2 \end{array}

Y finalmente representamos los puntos de la tabla de valores en la gráfica y trazamos la recta:

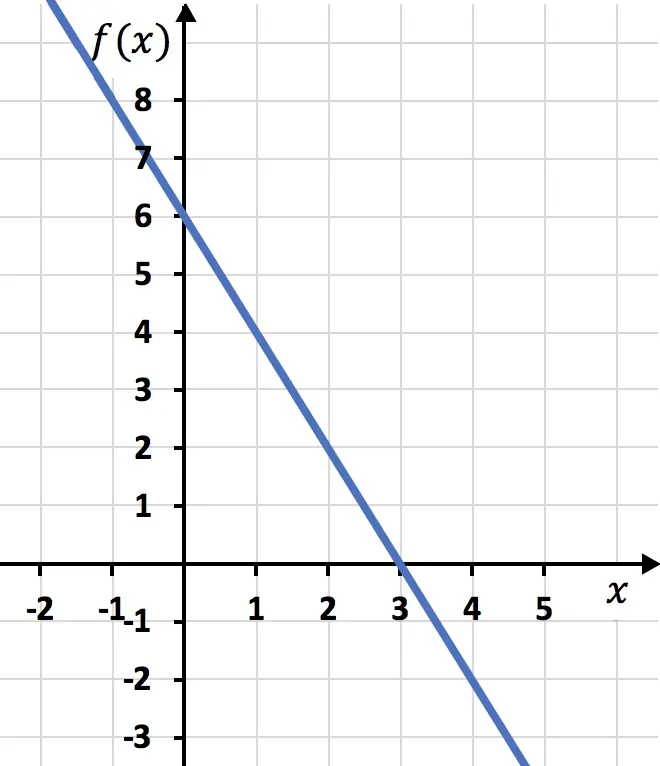
ejercicio resuelto paso a paso de funcion lineal y afin

 

Ejercicio 4

Encuentra la expresión de la función afín que pasa por los puntos (2,3) y (0,1).

La función pasa por los puntos (2,3) y (0,1), por tanto la pendiente de la función es:

m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{1-3}{0-2} = \cfrac{-2}{-2} = 1

Y la función será de la forma:

f(x)=mx+n \ \xrightarrow{m \ = \ 1} \ f(x)=1x+n

Una vez sabemos m podemos calcular n. Para ello debemos sustituir las coordenadas de un punto que pertenezca a la función en la ecuación. Por ejemplo el punto (2,3):

f(x)=x+n \ \xrightarrow{x \ = \ 2 \ ; \ f(x) \ = \ 3}   3=2+n

Ahora hay que resolver la ecuación resultante:

3-2=n

1 = n

De manera que la función corresponde a la siguiente expresión:

\bm{f(x)=x+1}

 

Ejercicio 5

Representa la siguiente función afín gráficamente:

f(x)=2x-1

Primero damos valores a x para crear la tabla de valores:

x= 0 \ \longrightarrow \ f(0)=2\cdot0-1=-1

x= 1 \ \longrightarrow \ f(1)=2\cdot1-1=1

x= 2 \ \longrightarrow \ f(2)=2\cdot2-1=3

x= 3 \ \longrightarrow \ f(3)=2\cdot3-1=5

x= 4 \ \longrightarrow \ f(4)=2\cdot4-1=7

\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}

Y después representamos los puntos de la tabla de valores en la gráfica y trazamos la recta:

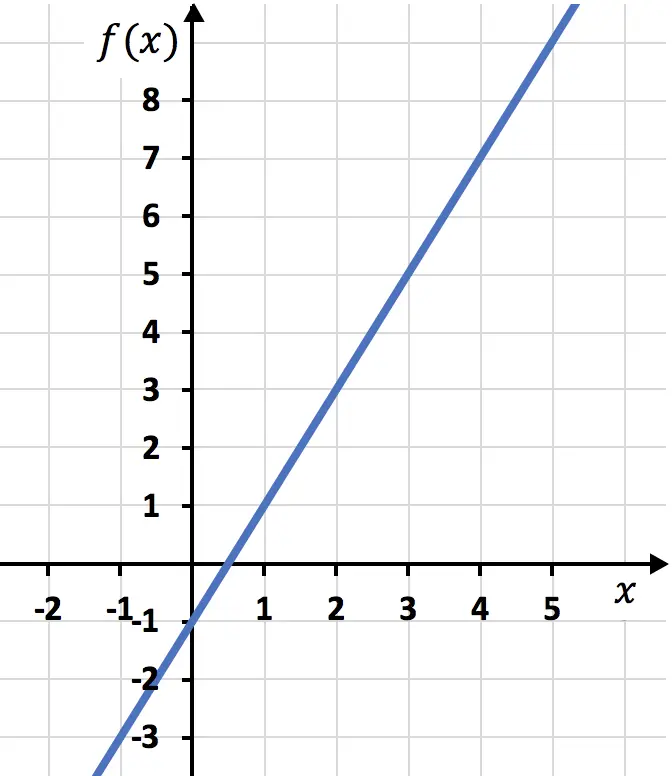
ejercicios resueltos de representar una funcion lineal o afin graficamente

 

Ejercicio 6

Calcula la función lineal que satisface las siguientes dos condiciones:

\begin{array}{c}f(3) =-2 \\[3ex] f(-1)=6 \end{array}

Que se cumpla f(3)=-2 quiere decir que la función pasa por el punto (3,-2). Y, del mismo modo, f(-1)=6 significa que la función pasa por el punto (-1,6).

De manera que la función pasa por los puntos (3,-2) y (-1,6), por lo que su pendiente es:

m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{6-(-2)}{-1-3} = \cfrac{8}{-4} = -2

Por tanto la función será de la forma:

f(x)=mx+n \ \xrightarrow{m \ = \ -2} \ f(x)=-2x+n

Y una vez sabemos m podemos calcular n. Para ello sustituimos las coordenadas de un punto que pertenezca a la función en la ecuación. Por ejemplo el punto (3,-2):

f(x)=-2x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ -2} \ -2=-2(3)+n

Y resolvemos la ecuación resultante:

-2=-6+n

-2+6=n

4 = n

Así que la función es:

\bm{f(x)=-2x+4}

 

Ejercicio 7

Halla la función afín que cumple f(1) =6  y pasa por el punto (3,5).

Que se cumpla f(1)=6 quiere decir que la función pasa por el punto (1,6).

De manera que la función pasa por los puntos (1,6) y (3,5) y, por tanto, su pendiente es:

m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{5-6}{3-1} = \cfrac{-1}{2} = -\cfrac{1}{2}

De manera que la función será de la forma:

\displaystyle f(x)=mx+n \ \xrightarrow{m \ = \ -\frac{1}{2}} \ f(x)=-\frac{1}{2}x+n

Una vez sabemos el término m podemos calcular el coeficiente n. Para ello sustituimos las coordenadas de un punto que pertenezca a la función en la ecuación. Por ejemplo el punto (1,6):

\displaystyle f(x)=-\frac{1}{2}x+n \ \xrightarrow{x \ = \ 1 \ ; \ f(x) \ = \ 6} \ 6=-\frac{1}{2}\cdot 1+n

Resolvemos la ecuación resultante:

6=-\cfrac{1}{2}+n

6+\cfrac{1}{2}=n

Recuerda que para sumar fracciones primero hay que reducirlas a común denominador y luego sumar los numeradores:

\cfrac{2 \cdot 6}{2} +\cfrac{1 \cdot 1}{2}=n

\cfrac{12}{2} +\cfrac{1}{2}=n

\cfrac{13}{2}=n

Por tanto la función es:

\displaystyle \bm{f(x)=-}\mathbf{\frac{1}{2}}\bm{x +}\mathbf{\frac{13}{2}}

 

Ejercicio 8

Resuelve el siguiente problema relacionado con las funciones lineales y afines:

Una tienda vende 40 unidades de un producto cuando el precio es de 15 €/unidad, y 65 unidades cuando el precio es 10 €/unidad.

  • Calcula la función de la demanda del producto, suponiendo que es una función afín.
  • ¿Cuántas unidades se venderán si se pone el precio a 12 €/unidad?

Como es una función afín, la función será del tipo f(x)=mx+n .

Donde x será el precio por unidad del producto y f(x) serán las unidades vendidas.

El enunciado nos dice que cuando el precio es 15 €/unidad se venden 40 unidades. Por tanto, como x es el precio y f(x) las unidades vendidas, se debe cumplir la siguiente igualdad:

f(15)=40

Y cuando el precio es 10 €/unidad se venden 65 unidades. Por tanto, usando el mismo razonamiento:

f(10)=65

Que se cumpla f(15)=40 quiere decir que la función pasa por el punto (15,40). Y f(10)=65 significa que la función pasa por el punto (10,65).

Por tanto la pendiente de la función es:

m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{65-40}{10-15} = \cfrac{25}{-5} = -5

De modo que la función será de la forma:

f(x)=mx+n \ \xrightarrow{m \ = \ -5} \ f(x)=-5x+n

Una vez sabemos m podemos calcular n. Para ello sustituimos las coordenadas de un punto que pertenezca a la función en la ecuación. Por ejemplo el punto (15,40):

f(x)=-5x+n \ \xrightarrow{x \ = \ 15 \ ; \ f(x) \ = \ 40} \ 40=-5\cdot 15+n

Y resolvemos la ecuación resultante:

40=-75+n

40+75=n

115 = n

Por tanto la función que relaciona las vendas producidas con el precio es:

\bm{f(x)=-5x+115}

Por otra parte, en la función x representa el precio. Por lo tanto, para saber cuántas unidades se venderán si el precio es 12 €/unidad debemos calcular f(12):

f(x)=-5x+115 \ \xrightarrow{x \ = \ 12} \ f(12)=-5\cdot 12+115

f(12)=-60+115

f(12)=\bm{55}

Así que si el precio es 12 €/unidad se venderán 55 unidades.

 

16 comentarios en “Función lineal y función afín”

  1. CESAR ADRIANO RAFAEL VÁSQUEZ

    Extraordinario, bastante claro, con ejemplos muy entendibles. Me gusta …. Gracias. Gracias.

    Responder
  2. jose

    ayuda para resolver este ejercicio por favor gracias, F(x)2x para x:4,3,2,10,-1,-2,-3,-4 X=2 y para y= -4-,-3,-2,-1-0, 1,2,3,4

    Responder
    1. Funciones

      Hola Jose, entiendo que debes graficar las dos funciones del ejercicio.

      La primera función, f(x)=2x, es una función lineal. Por lo tanto, tienes que calcular la imagen de la función en cada punto y representar los puntos obtenidos en una gráfica, tal y como se explica en este artículo. Luego solo tienes que unir los puntos calculados.

      La segunda función, x=2y, la han expresado diferente pero el proceso es exactamente el mismo. Primero calculas las imágenes de la función en los puntos dados, luego representas los puntos en la gráfica, y finalmente los unes trazando una línea recta.

    1. Funciones

      ¡Gracias Marcela! Todos los artículos están explicados lo mejor posible. 😊

    1. Funciones

      ¡Muchísimas gracias Daniel! ¡Se ha puesto el máximo esfuerzo en todos los artículos! 😉

    1. Funciones

      Hola Liliana,

      La función que propones es la función opuesta a la función identidad, por lo tanto, para graficar la función simplemente debes dibujar una recta con una pendiente de -1 y que pase por el origen de coordendadas.

  8. mariluz

    consulta, en el ejemplo de como representar funciones, mencionas que es una función lineal, sin embargo me cabe la duda ya que se supone que la función lineal no tiene coeficiente de posición??? ayudaaaa por favor..estoy confundida

    Responder
    1. Funciones

      Hola Mariluz,

      Efectivamente, la función representada en el ejemplo que mencionas es una función afín, ya que tiene ordenada en el origen. Ya se ha corregido este pequeño detalle, ¡gracias por tu aportación!

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *