▷ Cómo representar una función (ejercicios resueltos)

En este post veremos cómo representar en una gráfica cualquier tipo de función. Además, encontrarás ejercicios resueltos paso a paso de la representación de funciones en una gráfica.

Índice

Cómo representar una función en una gráfica

Para representar una función en una gráfica, se deben hacer los siguientes pasos:

Hallar el dominio de la función.
Calcular los puntos de corte de la función con los ejes cartesianos.
Calcular las asíntotas de la función.
Estudiar la monotonía de la función y hallar sus extremos relativos.
Estudiar la curvatura de la función y hallar sus puntos de inflexión.
Representar en la gráfica los puntos de corte, las asíntotas, los extremos relativos y los puntos de inflexión, y luego trazar la función.

Ejemplo de la representación de una función

Para que veas cómo se representa una función gráficamente, vamos a resolver el siguiente ejercicio paso a paso:

Representa en un gráfico la siguiente función racional:

$f(x)=\cfrac{x^2}{x-1}$

Lo primero que debemos hacer es calcular el dominio de la función. Se trata de una función racional, por tanto, tenemos que igualar a cero el denominador para ver qué números no pertenecen al dominio de la función:

$x-1=0$

$x=1$

De modo que cuando x sea 1 el denominador será 0 y, en consecuencia, la función no existirá. Así que el domino de la función son todos los números reales excepto x=1.

$\text{Dom } f= \mathbb{R}-\{1 \}$

Para hallar el punto de corte con el eje X, debemos resolver la ecuación $f(x)= 0.$ Ya que la función siempre vale 0 en el eje X:

$f(x)=0$

$\cfrac{x^2}{x-1} = 0$

El término $x -1$ está dividiendo todo el lado izquierdo, por tanto, lo podemos pasar multiplicando a todo el lado derecho:

$x^2 = 0 \cdot (x-1)$

$x^2 = 0$

$x = 0$

De manera que el punto de corte con el eje OX es:

$\bm{(0,0)}$

Y para hallar el punto de corte con el eje Y, calculamos $f(0).$ Porque x siempre vale 0 en el eje Y:

$f(0)=\cfrac{0^2}{0-1} = \cfrac{0}{-1} = 0$

Por tanto, el punto de corte con el eje OY es:

$\bm{(0,0)}$

En este caso, como la función pasa por el origen de coordenadas, el punto de corte con el eje X coincide con el punto de corte con el eje Y.

Ua vez sabemos el dominio y los puntos de corte, debemos calcular las asíntotas de la función.

Para ver si la función tiene alguna asíntota vertical, tenemos que calcular el límite de la función en los puntos que no pertenecen al dominio (en este caso x=1). Y si el resultado es infinito, se trata de una asíntota vertical. Por tanto:

$\displaystyle \lim_{x \to 1} \ \cfrac{x^2}{x-1} = \cfrac{1^2}{1-1} = \cfrac{1}{0} = \infty$

Como el límite de la función cuando x tiende a 1 da infinito, x=1 es una asíntota vertical:

representar funciones, asintota vertical

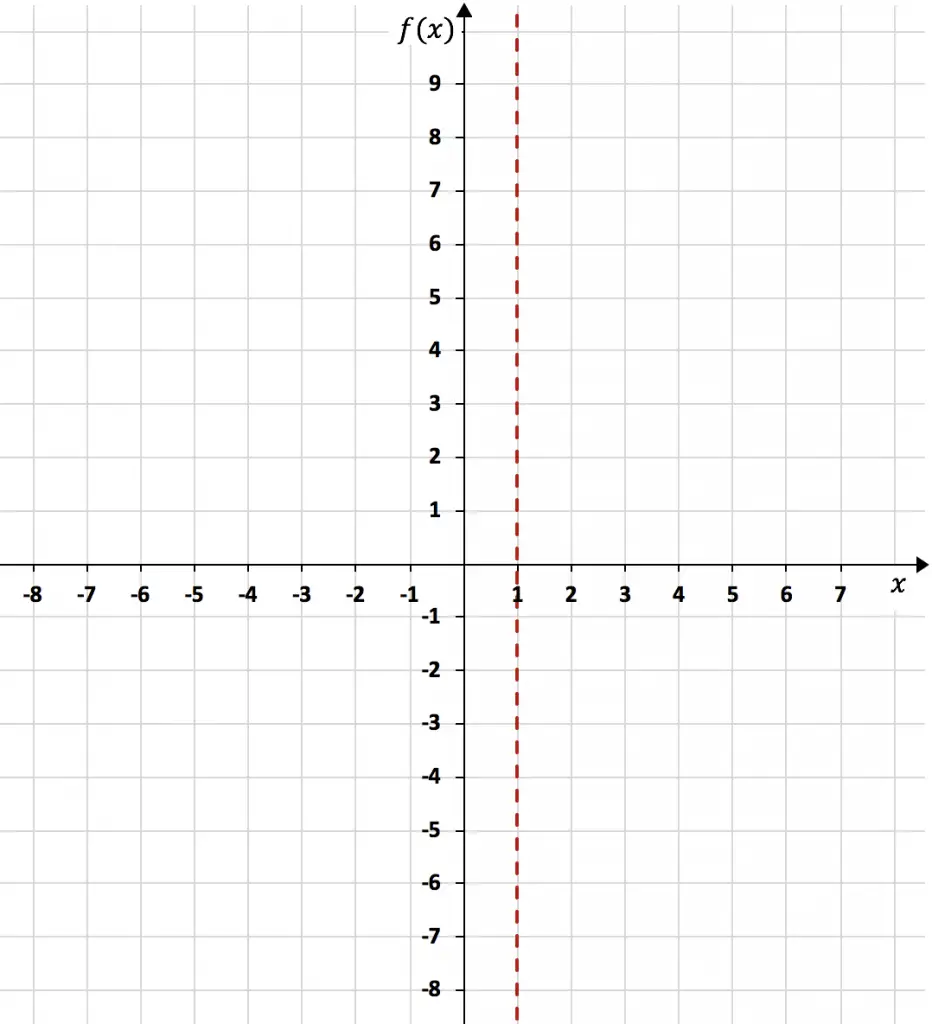
Una vez calculada la asíntota vertical, tenemos que calcular los límites laterales de la función hacia ella. Ya que no sabemos si la función tenderá a -∞ o a +∞ cuando se acerque a x=1 por la izquierda, y tampoco lo sabemos cuando se acerque a x=1 por la derecha.

Así pues, procedemos a calcular el límite lateral por la izquierda de la función en x=1:

$\displaystyle \lim_{x \to 1^{-}} \cfrac{x^2}{x-1}$

Para calcular numéricamente un límite lateral en un punto, tenemos que sustituir en la función un número que se acerque mucho al punto. En este caso queremos un número que se acerque mucho a 1 por la izquierda, como por ejemplo el 0,9. Así que sustituimos el punto 0,9 en la función:

$\cfrac{0,9^2}{0,9-1}=\cfrac{0,81}{-0,1}=-81$

Los límites laterales en una asíntota solo pueden dar +∞ o -∞. Y como al sustituir en la función un número que se acerca mucho a 1 por la izquierda hemos obtenido un resultado negativo, el límite por la izquierda es -∞:

$\displaystyle \lim_{x \to 1^{-}} \cfrac{x^2}{x-1} = \bm{-\infty}$

Ahora hacemos el mismo procedimiento con el límite lateral por la derecha:

$\displaystyle \lim_{x \to 1^{+}} \cfrac{x^2}{x-1}$

Sustituimos en la función un número que se acerque mucho a 1 por la derecha. Por ejemplo el punto 1,1:

$\cfrac{1,1^2}{1,1-1}=\cfrac{1,21}{0,1}=+12,1$

En este caso el resultado del límite lateral es un número positivo. Por lo tanto, el límite por la derecha es +∞:

$\displaystyle \lim_{x \to 1^{+}} \cfrac{x^2}{x-1} = \bm{+\infty}$

En conclusión, en x=1 la función tiende a menos infinito por la izquierda, y a más infinito por la derecha:

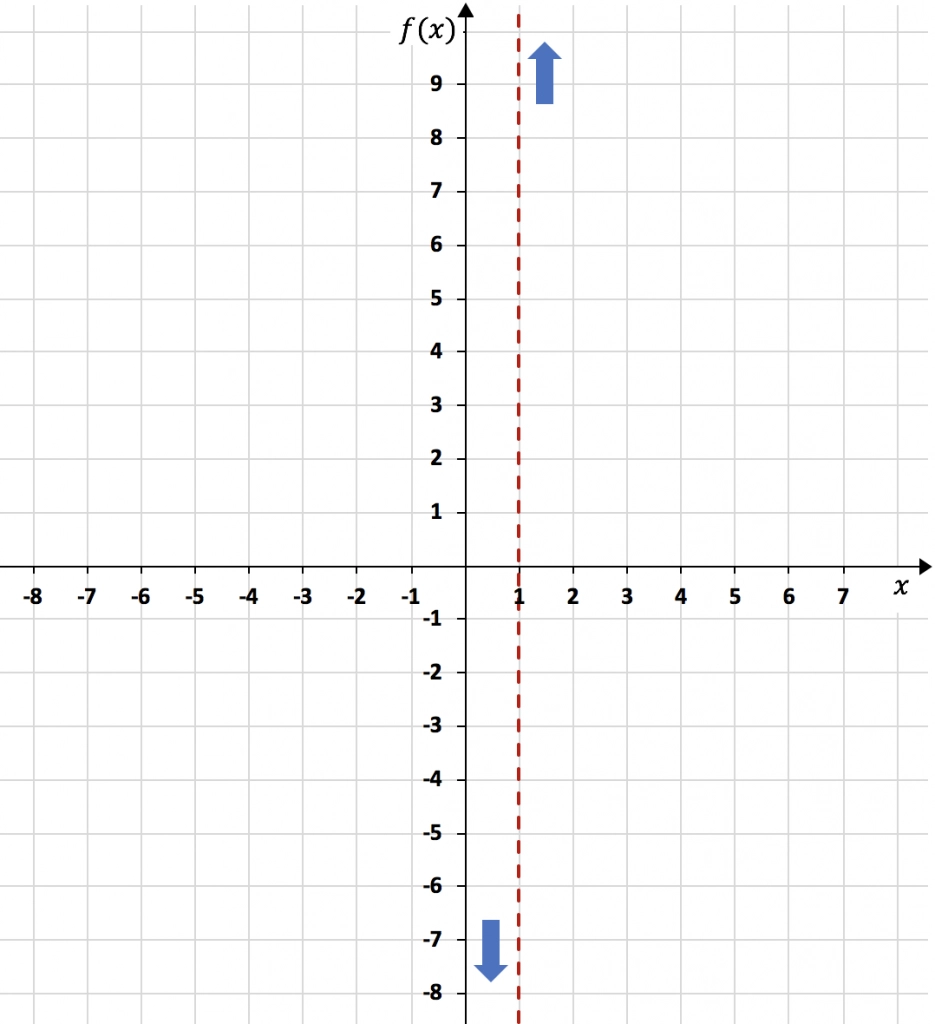
Por otro lado, la asíntota horizontal de la función será el resultado del límite al infinito de la función. Por tanto:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^2}{x-1} = \cfrac{+\infty}{+\infty } =+\infty$

Recuerda cómo calcular límites al infinito de funciones racionales:

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex] \cfrac{a_n}{b_n} & \text{si} & r=s \\[5ex] \pm \infty & \text{si} & r>s \end{array}\right.$

El límite al infinito de la función nos ha dado +∞, por tanto, la función no tiene asíntota horizontal.

Ahora calculamos la asíntota oblicua. Las asíntotas oblicuas son de la forma $y=mx+n$ . Y $m$ se calcula con la siguiente fórmula:

$\displaystyle m = \lim_{x \to +\infty} f(x):x$

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2}{x-1}:x$

La x es como si tuviera un 1 como denominador:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2}{x-1}:\cfrac{x}{1}$

Se trata de una división de fracciones, por tanto, las multiplicamos en cruz:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 \cdot 1 }{(x-1) \cdot x}$

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 }{x^2-x}$

Y calculamos el límite:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 }{x^2-x} = \cfrac{+\infty}{+\infty } = \cfrac{1}{1} = 1$

De manera que m=1. Ahora calculamos $n$ con la siguiente fórmula:

$\displaystyle n = \lim_{x \to +\infty} \bigl[f(x)-mx\bigr]$

$\displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-1x\right] = \cfrac{+\infty}{+\infty} -(+\infty) = +\infty - \infty$

Pero obtenemos la indeterminación infinito menos infinito, por lo que debemos reducir los términos a común denominador. Para ello, multiplicamos y dividimos el término x por el denominador de la fracción:

$\displaystyle n = \lim_{x \to +\infty}\left[\cfrac{x^2}{x-1}-x\right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x\cdot (x-1)}{x-1} \right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x^2-x}{x-1}\right]$

Ahora que los dos términos tienen el mismo denominador, los podemos juntar:

$\displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2-(x^2-x)}{x-1} \right] =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right]$

Y finalmente resolvemos el límite:

$\displaystyle n =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right] = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = 1$

De modo que n=1. Por tanto, la asíntota oblicua es:

$y = mx+n$

$y = 1x+1$

$\bm{y = x+1}$

Una vez hemos calculado la asíntota oblicua, la representamos en la misma gráfica haciendo una tabla de valores:

$y=x+1$

$\begin{array}{c|c} x & y \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \end{array}$

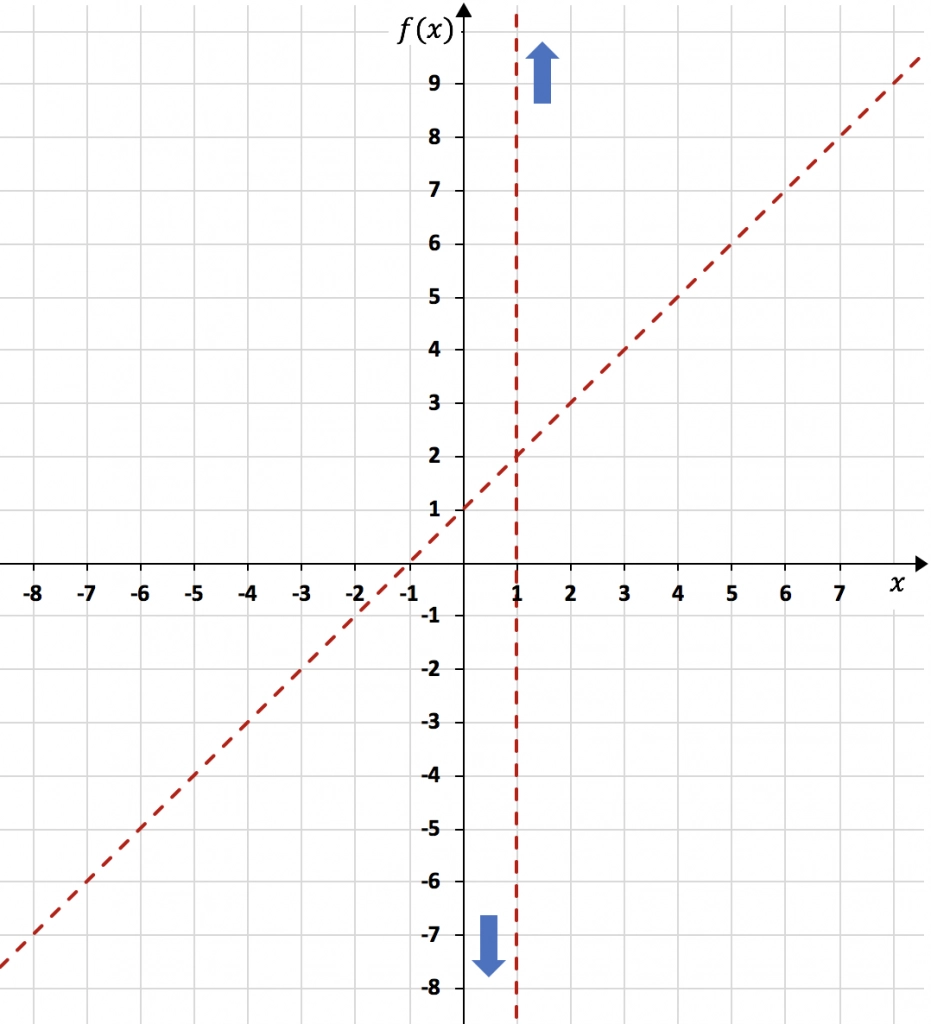
Ahora que ya sabemos todas las asíntotas que tiene la función, tenemos que analizar la monotonía de la función. Es decir, debemos estudiar en qué intervalos la función crece y en qué intervalos decrece. Así que calculamos la primera derivada de la función:

$f(x)=\cfrac{x^2}{x-1} \ \longrightarrow \ f'(x)= \cfrac{2x\cdot (x-1) - x^2 \cdot 1}{(x-1)^2}$

$f'(x)= \cfrac{2x^2-2x - x^2}{(x-1)^2} = \cfrac{x^2-2x}{(x-1)^2}$

Y ahora igualamos la derivada a 0 y resolvemos la ecuación:

$f'(x)=0$

$\cfrac{x^2-2x}{(x-1)^2}=0$

El término $\left(x-1\right)^2}$ está dividiendo a todo el lado izquierdo, por tanto, lo podemos pasar multiplicando a todo el lado derecho:

$x^2-2x=0\cdot \left(x-1\right)^2$

$x^2-2x=0$

Extraemos factor común para resolver la ecuación cuadrática:

$x(x-2)=0$

Para que la multiplicación valga 0, uno de los dos elementos de la multiplicación tiene que ser cero. Por lo tanto, igualamos cada factor a 0 y obtenemos las dos soluciones de la ecuación:

$\displaystyle x\cdot(x-2) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] x-2=0 \ \longrightarrow \ \bm{x= 2} \end{cases}$

Ahora representamos en la recta numérica todos los puntos críticos encontrados, es decir, los puntos que no pertenecen al dominio (x=1) y los que anulan la derivada (x=0 y x=2):

Y evaluamos el signo de la derivada en cada intervalo, para saber si la función crece o decrece. De manera que cogemos un punto de dentro de cada intervalo (nunca los puntos críticos) y miramos qué signo tiene la derivada en ese punto:

$f'(x)=\cfrac{x^2-2x}{\left(x-1\right)^2}$

$f'(-1) = \cfrac{(-1)^2-2(-1)}{\left((-1)-1\right)^2} =\cfrac{+3}{+4} = +0,75 \ \rightarrow \ \bm{+}$

$f'(0,5) = \cfrac{0,5^2-2\cdot 0,5}{\left(0,5-1\right)^2} = \cfrac{-0,75}{+0,25} = -3 \ \rightarrow \ \bm{-}$

$f'(1,5) = \cfrac{1,5^2-2\cdot 1,5}{\left(1,5-1\right)^2} = \cfrac{-0,75}{+0,25} = -3 \ \rightarrow \ \bm{-}$

$f'(3) = \cfrac{3^2-2\cdot 3}{\left(3-1\right)^2} =\cfrac{+3}{+4} = +0,75 \ \rightarrow \ \bm{+}$

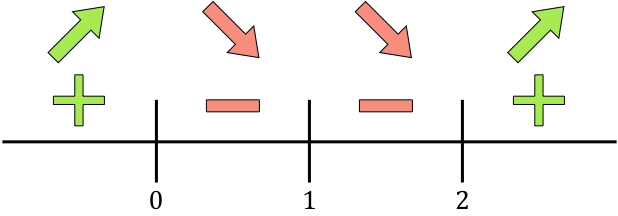
Si la derivada es positiva significa que la función crece, y si la derivada es negativa significa que la función decrece. Por tanto, los intervalos de crecimiento y decrecimiento son:

Crecimiento: $\bm{(-\infty, 0)\cup (2,+\infty)}$

Decrecimiento: $\bm{(0,1)\cup (1,2)}$

Además, en x=0 la función pasa de ser creciente a ser decreciente, así que x=0 es un máximo relativo de la función. Y en x=2 la función pasa de ser decreciente a ser creciente, por lo que x=2 es un mínimo relativo de la función.

Finalmente, sustituimos los extremos encontrados en la función original para hallar la coordenada Y de los puntos:

$f(0)=\cfrac{0^2}{0-1} = \cfrac{0}{-1} = 0 \ \longrightarrow \ (0,0)$

$f(2)=\cfrac{2^2}{2-1} = \cfrac{4}{1} = 4 \ \longrightarrow \ (2,4)$

Así que los extremos relativos de la función son:

Máximo en el punto $\bm{(0,0)}$

Mínimo en el punto $\bm{(2,4)}$

Representamos el máximo y el mínimo en el gráfico:

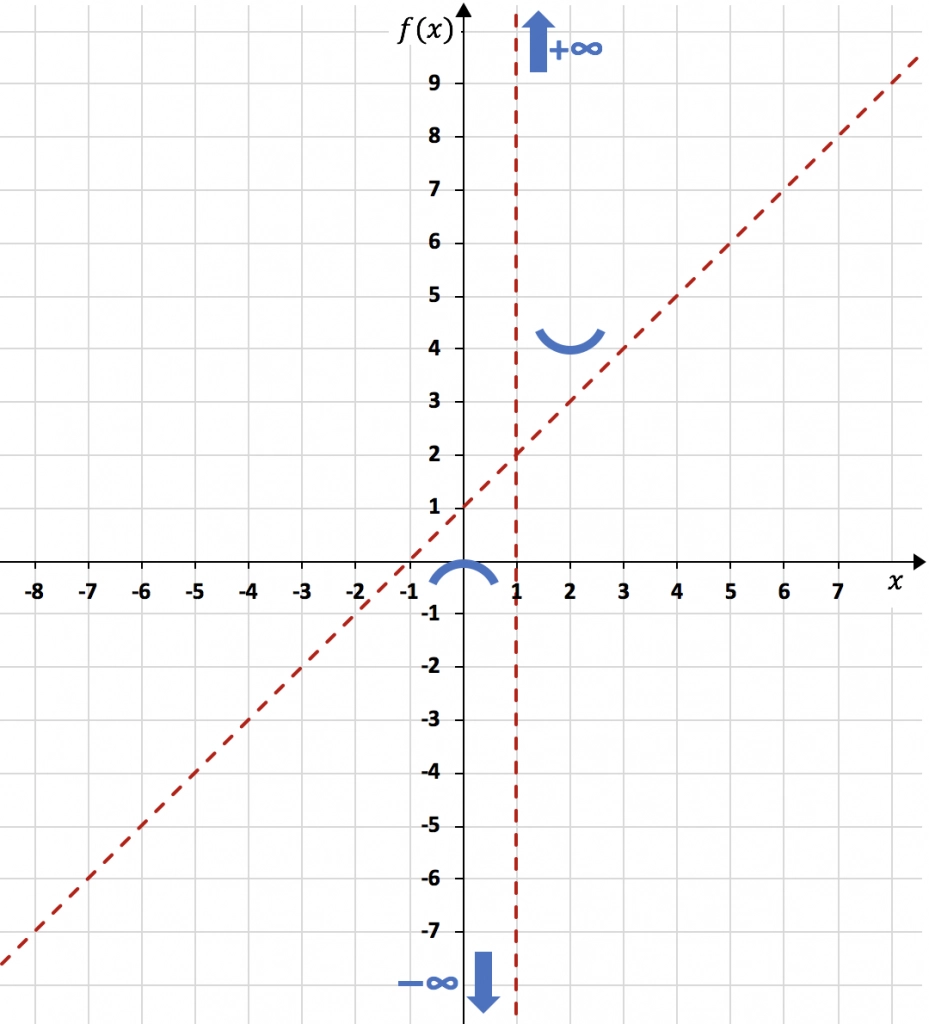
Finalmente, solo nos queda estudiar la curvatura de la función, es decir, estudiar los intervalos de concavidad y convexidad de la función. Para ello, calculamos su segunda derivada:

$f'(x)=\cfrac{x^2-2x}{(x-1)^2} \ \longrightarrow \ f''(x)= \cfrac{(2x-2)\cdot (x-1)^2- (x^2-2x)\cdot 2(x-1)\cdot 1}{\left(\left(x-1\right)^2\right)^2}$

$f''(x)= \cfrac{(2x-2)\cdot (x-1)^2- (x^2-2x)\cdot 2(x-1)}{(x-1)^4}$

$f''(x)= \cfrac{(2x-2)\cdot (x-1)^{\cancel{2}}- (x^2-2x)\cdot 2\cancel{(x-1)}}{(x-1)^{\cancelto{3}{4}}} = \cfrac{(2x-2)\cdot (x-1)- (x^2-2x)\cdot 2}{(x-1)^3}$

$f''(x)= \cfrac{2x^2-2x-2x+2- (2x^2-4x)}{(x-1)^3} =\cfrac{2x^2-2x-2x+2- 2x^2+4x}{(x-1)^3}$

$f''(x) =\cfrac{2}{(x-1)^3}$

Y ahora igualamos la segunda derivada a cero y resolvemos la ecuación:

$f''(x)=0$

$\cfrac{2}{(x-1)^3} =0$

$2=0\cdot \left(x-1\right)^3$

$2=0$

2 nunca será igual a 0, por lo que la ecuación $f''(x)=0$ no tiene solución.

Ahora representamos en la recta numérica todos los puntos críticos encontrados, es decir, los puntos que no pertenecen al dominio (x=1) y los que anulan la segunda derivada (en este caso no hay):

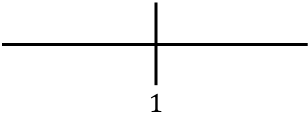
Y evaluamos el signo de la derivada en cada intervalo, para saber si la función es convexa o cóncava. De manera que cogemos un punto de dentro de cada intervalo (nunca los puntos singulares) y miramos qué signo tiene la derivada en ese punto:

$f''(x) =\cfrac{2}{(x-1)^3}$

$f''(0) =\cfrac{2}{(0-1)^3} = \cfrac{2}{-1}=-2 \ \rightarrow \ \bm{-}$

$f''(2) =\cfrac{2}{(2-1)^3} = \cfrac{2}{1}=2 \ \rightarrow \ \bm{+}$

Y finalmente deducimos los intervalos de concavidad y convexidad de la función. Si la segunda derivada es positiva significa que la función es convexa $(\bm{\cup})$ , y si la segunda derivada es negativa significa que la función es cóncava $(\bm{\cap})$ . Por tanto, los intervalos de concavidad y convexidad son:

Convexa $(\bm{\cup})$ : $\bm{(1,+\infty)}$

Cóncava $(\bm{\cap})$ : $\bm{(-\infty,1)}$

Sin embargo, aunque haya un cambio de curvatura en x=1, este no es un punto de inflexión. Porque x=1 no pertenece al dominio de la función.

Por tanto, podemos acabar de representar la función con la ayuda de todo lo que hemos calculado:

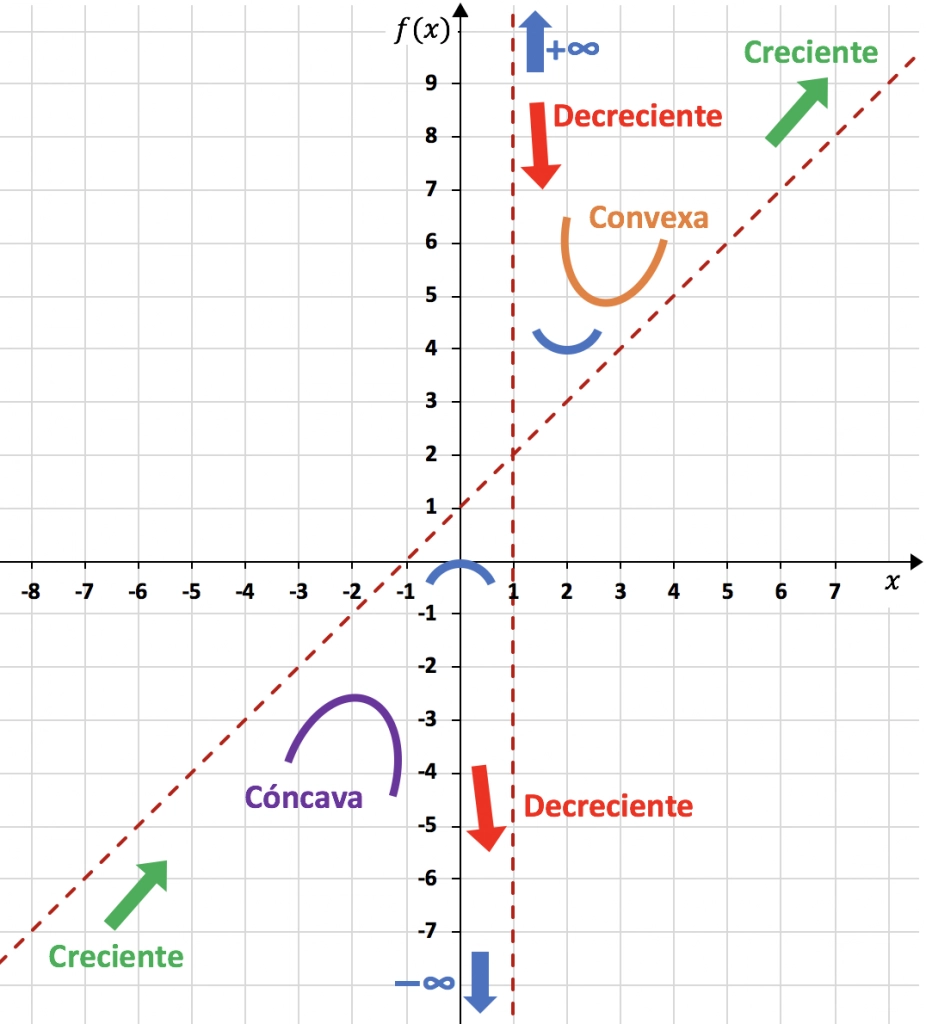
De manera que la función representada en la gráfica queda de la siguiente manera:

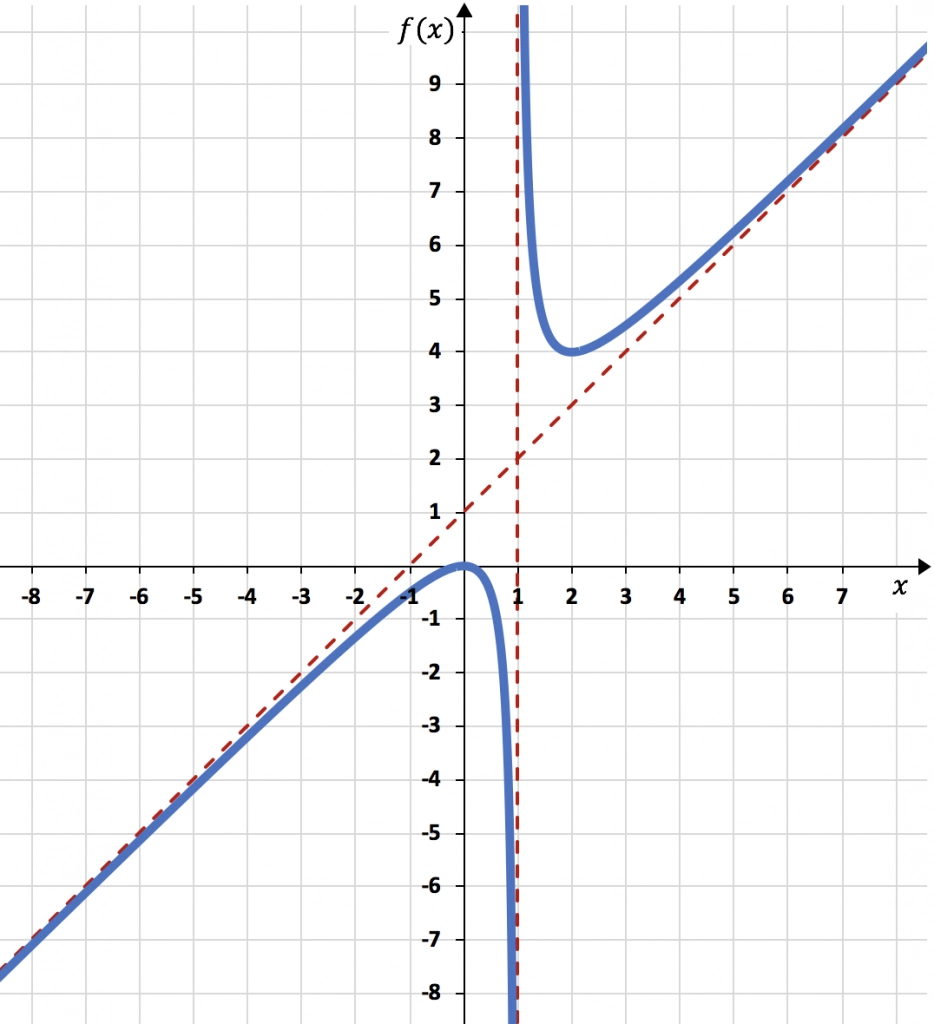
representacion grafica de funcion racional

Ejercicios resueltos de representación de funciones

Ejercicio 1

Representa en una gráfica la siguiente función polinómica:

$\displaystyle f(x)=x^3-3x^2+4$

Ver solución

Lo primero que debemos hacer es calcular el dominio de la función. Se trata de una función polinómica, por tanto, el dominio son todos los números reales:

$\text{Dom } f= \mathbb{R}$

Para hallar el punto de corte con el eje X, resolvemos $f(x)= 0.$

$f(x)=0$

$x^3-3x^2+4=0$

Se trata de una ecuación de grado superior a 2. Por tanto, factorizamos la ecuación:

$(x+1)(x^2-4x+4)=0$

De manera que x=-1 es una solución. Y calculamos las otras soluciones resolviendo la ecuación de segundo grado resultante:

$\begin{aligned}x & =\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} =\cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1 \cdot 4}}{2\cdot 1} \\[2ex] &=\cfrac{+4 \pm \sqrt{16-16}}{2} =\cfrac{4 \pm \sqrt{0}}{2} = \cfrac{4 }{2 } = 2\end{aligned}$

Por tanto, los puntos de corte con el eje X son:

$\bm{(-1,0)}$ y $\bm{(2,0)}$

Y para hallar el punto de corte con el eje Y, calculamos $f(0).$ Ya que x siempre vale 0 en el eje Y:

$f(0)=0^3-3\cdot0^2+4 = 4$

Por tanto, el punto de corte con el eje Y es:

$\bm{(0,4)}$

Para ver si la función tiene alguna asíntota vertical, tenemos que calcular el límite de la función en los puntos que no pertenecen al dominio. En este caso el dominio incluye a todos los números reales. Así que la función no tiene ninguna asíntota vertical.

Por otro lado, la asíntota horizontal de la función será el resultado del límite al infinito de la función. Por tanto:

$\displaystyle \lim_{x \to +\infty} \ x^3-3x^2+4 =(+\infty)^3 = +\infty$

El límite al infinito de la función nos ha dado +∞, por tanto, la función no tiene asíntota horizontal.

Ahora calculamos la asíntota oblicua. Las asíntotas oblicuas son de la forma $y=mx+n.$ Y $m$ se calcula con la siguiente fórmula:

$\displaystyle m = \lim_{x \to +\infty} f(x):x = \lim_{x \to +\infty} \left( x^3-3x^2+4\right): x =$

$\displaystyle = \lim_{x \to +\infty} \cfrac{x^3-3x^2+4}{x} = \cfrac{+\infty}{+\infty} = +\infty$

El límite nos ha dado +∞, de modo que la función tampoco tiene asíntota oblicua.

Para estudiar la monotonía de la función, primero debemos calcular su derivada:

$f(x)= x^3-3x^2+4 \ \longrightarrow \ f'(x)= 3x^2-6x$

Ahora igualamos la derivada a 0 y resolvemos la ecuación:

$f'(x)= 0$

$3x^2-6x=0$

$x(3x-6)=0$

$\displaystyle x\cdot(3x-6) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] 3x-6=0 \ \longrightarrow \ x= \cfrac{6}{3} = 2 \end{cases}$

Ahora representamos en la recta numérica todos los puntos singulares obtenidos, es decir, los puntos que no pertenecen al dominio (en este caso pertenecen todos) y los que anulan la derivada (x=0 y x=2):

Y evaluamos el signo de la derivada en cada intervalo, para saber si la función crece o decrece. De manera que cogemos un punto de dentro de cada intervalo (nunca los puntos singulares) y miramos qué signo tiene la derivada en ese punto:

$f'(-1)=3(-1)^2-6(-1)= 3+6 = 9\ \rightarrow \ \bm{+}$

$f'(1)=3\cdot 1^2-6\cdot 1= 3-6 = -3\ \rightarrow \ \bm{-}$

$f'(3)=3\cdot 3^2-6\cdot 3= 27-18 = 9\ \rightarrow \ \bm{+}$

Si la derivada es positiva significa que la función crece, y si la derivada es negativa significa que la función decrece. Por tanto, los intervalos de crecimiento y decrecimiento son:

Crecimiento: $\bm{(-\infty,0)\cup (2,+\infty)}$

Decrecimiento: $\bm{(0,2)}$

La función pasa de ser creciente a ser decreciente en x=0, así que x=0 es un máximo de la función. Y la función pasa de ser decreciente a ser creciente en x=2, por lo que x=2 es un mínimo de la función.

Por último, sustituimos los extremos encontrados en la función original para hallar las coordenadas Y de los puntos:

$f(0)=0^3-3\cdot 0^2+4 = 4 \ \longrightarrow \ (0,4)$

$f(2)=2^3-3\cdot 2^2+4 = 8-3 \cdot 4 +4 = 0 \ \longrightarrow \ (2,0)$

Así que los extremos relativos de la función son:

Máximo en el punto $\bm{(0,4)}$

Mínimo en el punto $\bm{(2,0)}$

Para estudiar la curvatura de la función, calculamos su segunda derivada:

$f'(x)= 3x^2-6x \ \longrightarrow \ f''(x)= 6x-6$

Ahora igualamos la segunda derivada a 0 y resolvemos la ecuación:

$f''(x)= 0$

$6x-6=0$

$6x=6$

$x= \cfrac{6}{6} = 1$

Representamos en la recta todos los puntos singulares encontrados, es decir, los puntos que no pertenecen al dominio (en este caso pertenecen todos) y los que anulan la derivada (x=1):

Y ahora evaluamos el signo de la segunda derivada en cada intervalo, para saber si la función es cóncava o convexa. De manera que cogemos un punto de dentro de cada intervalo (nunca los puntos singulares) y miramos qué signo tiene la segunda derivada en ese punto:

$f''(0)=6\cdot 0-6= -6 \ \rightarrow \ \bm{-}$

$f''(2)=6\cdot 2-6= 12-6= 6 \ \rightarrow \ \bm{+}$

Si la segunda derivada es positiva significa que la función es convexa $(\bm{\cup})$ , y si la segunda derivada es negativa significa que la función es cóncava $(\bm{\cap})$ . Por tanto, los intervalos de concavidad y convexidad son:

Convexa $(\bm{\cup})$ : $\bm{(1,+\infty)}$

Cóncava $(\bm{\cap})$ : $\bm{(-\infty,1)}$

Además, la función pasa de ser cóncava a ser convexa en x=1, por lo que x=1 es un punto de inflexión de la función.

Por último, sustituimos los puntos de inflexión encontrados en la función original para hallar la coordenada Y de los puntos:

$f(1)=1^3-3\cdot 1^2+ 4= 1 -3 +4 =2 \ \longrightarrow \ (1,2)$

Así que los puntos de inflexión de la función son:

Puntos de inflexión: $\bm{(1,2)}$

Finalmente, a partir de toda la información que hemos calculado, representamos gráficamente la función:

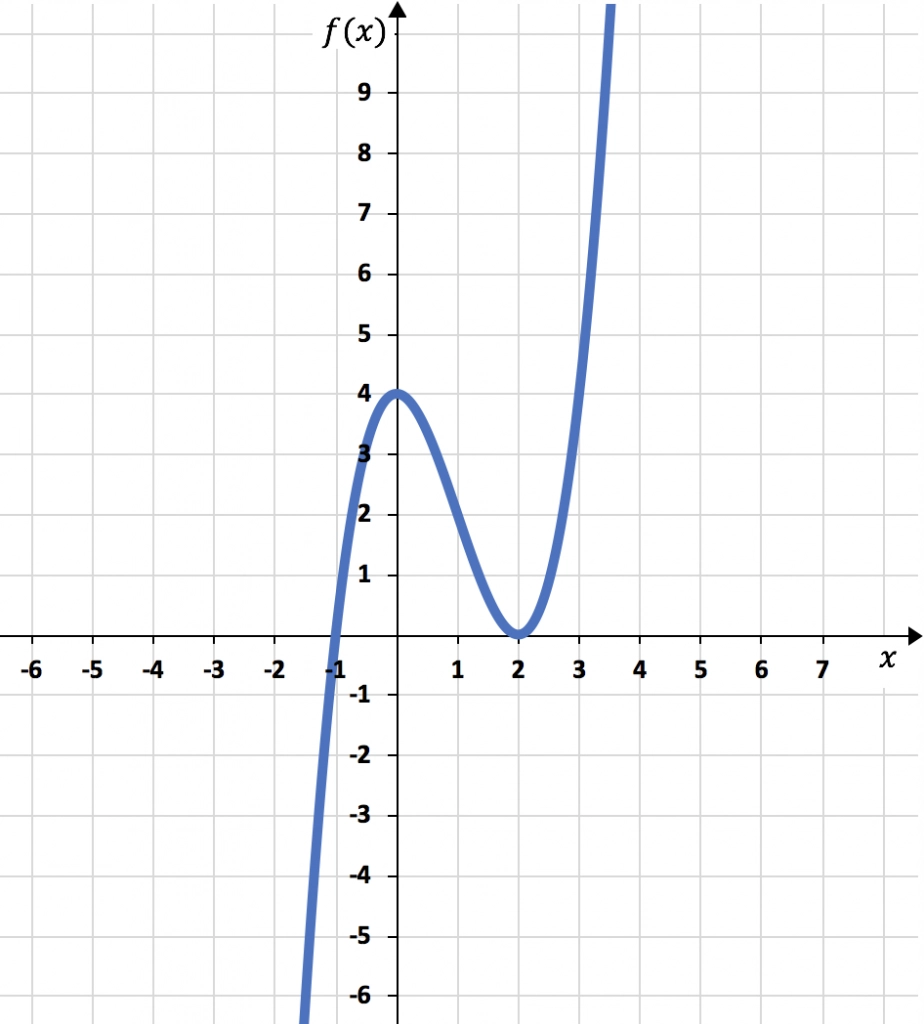
representacion grafica funcion polinomica

Ejercicio 2

Representa gráficamente la siguiente función racional:

$\displaystyle f(x)=\frac{x^2+2}{x^2-1}$

Ver solución

Para hallar el dominio de la función, igualamos el denominador. deal fracción a cero y resolvemos la ecuación resultante:

$x^2-1= 0$

$x^2=1$

$\sqrt{x^2}=\sqrt{1}$

$x=\pm 1$

$\text{Dom } f= \mathbb{R}-\{-1, +1 \}$

En segundo lugar, determinamos los puntos de corte de la función con el eje de abscisas igualando la expresión algebraica de la función. acero:

$f(x)=0$

$\cfrac{x^2+2}{x^2-1}=0$

$x^2+2=0\cdot (x^2-1)$

$x^2+2=0$

$x^2=-2$

$x=\sqrt{-2} \quad \color{red}\bm{\times}$

No existe la raíz cuadrada de un número negativo. Por tanto, la función no corta el eje X.

Y para hallar el punto de corte con el eje de las ordenadas, evaluamos la función en x=0.

$f(0)=\cfrac{0^2+2}{0^2-1}= \cfrac{2}{-1} = -2$

Por tanto, el punto de corte con el eje Y es:

$\bm{(0,-2)}$

Para ver si la función tiene alguna asíntota vertical, tenemos que calcular el límite de la función en los puntos que no pertenecen al dominio (en este caso x=-1 y x=+1). Y si el resultado es infinito, se trata de una asíntota vertical. Por tanto:

$\displaystyle \lim_{x \to -1} \cfrac{x^2+2}{x^2-1} = \cfrac{(-1)^2+2}{(-1)^2-1} =\cfrac{1+2}{1-1}= \cfrac{3}{0} = \infty$

Como el límite de la función cuando x tiende a -1 da infinito, x=-1 es una asíntota vertical.

Calculamos los límites laterales de la asíntota x=-1 sustituyendo en la función un número que se le acerque mucho:

$\displaystyle f(-1,1)=\cfrac{(-1,1)^2+2}{(-1,1)^2-1} =+15,29 \longrightarrow \lim_{x \to -1^{-}} \ \cfrac{x^2+2}{x^2-1} = +\infty$

$\displaystyle f(-0,9)=\cfrac{(-0,9)^2+2}{(-0,9)^2-1} =-14,79 \longrightarrow \lim_{x \to -1^{+}} \ \cfrac{x^2+2}{x^2-1} = -\infty$

Miramos ahora si x=+1 es una asíntota vertical:

$\displaystyle \lim_{x \to +1} \cfrac{x^2+2}{x^2-1} = \cfrac{1^2+2}{1^2-1} =\cfrac{1+2}{1-1}= \cfrac{3}{0} = \infty$

Como el límite de la función cuando x tiende a +1 da infinito, x=+1 es una asíntota vertical.

Calculamos los límites laterales de la asíntota x=1 sustituyendo en la función un número que se le acerque mucho:

$\displaystyle f(0,9)=\cfrac{(0,9)^2+2}{(0,9)^2-1} =-14,79 \longrightarrow \lim_{x \to +1^{-}} \ \cfrac{x^2+2}{x^2-1} = -\infty$

$\displaystyle f(1,1)=\cfrac{(1,1)^2+2}{(1,1)^2-1} =+15,29 \longrightarrow \lim_{x \to +1^{+}} \ \cfrac{x^2+2}{x^2-1} = +\infty$

Por otro lado, la asíntota horizontal de la función será el resultado del límite al infinito de la función. Por tanto:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^2+2}{x^2-1} = \cfrac{+\infty}{+\infty } =\cfrac{1}{1} = 1$

El límite al infinito de la función nos ha dado 1, por tanto, la función tiene una asíntota horizontal en y=1.

Como la función tiene asíntota horizontal, no tendrá asíntota oblicua.

Derivamos la función para luego estudiar los intervalos de crecimiento y decrecimiento:

$f(x)=\cfrac{x^2+2}{x^2-1} \ \longrightarrow \ f'(x)= \cfrac{2x \cdot (x^2-1) -(x^2+2) \cdot 2x}{\left(x^2-1 \right)^2}$

$f'(x)= \cfrac{2x^3-2x - (2x^3+4x) }{\left(x^2-1 \right)^2} = \cfrac{-6x}{\left(x^2-1 \right)^2}$

Ahora igualamos la derivada a 0 y resolvemos la ecuación:

$f'(x)= 0$

$\cfrac{-6x}{\left(x^2-1 \right)^2}=0$

$-6x=0\cdot\left(x^2-1 \right)^2$

$-6x= 0$

$x=\cfrac{0}{-6} = 0$

Representamos en la recta todos los puntos críticos calculados, que son los puntos que no pertenecen al dominio (x=-1 y x=+1) y los que anulan la derivada (x=0):

$f'(-2)= \cfrac{-6(-2)}{\left((-2)^2-1 \right)^2} = \cfrac{12}{9} =1,33 \ \rightarrow \ \bm{+}$

$f'(-0,5)= \cfrac{-6(-0,5)}{\left((-0,5)^2-1 \right)^2} = \cfrac{3}{0,56} =5,33 \ \rightarrow \ \bm{+}$

$f'(0,5)= \cfrac{-6\cdot 0,5}{\left(0,5^2-1 \right)^2} = \cfrac{-3}{0,56} =-5,33 \ \rightarrow \ \bm{-}$

$f'(2)= \cfrac{-6\cdot 2}{\left(2^2-1 \right)^2} = \cfrac{-12}{9} =-1,33 \ \rightarrow \ \bm{-}$

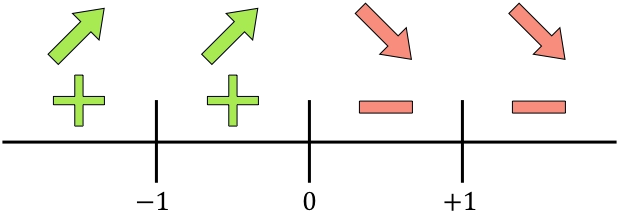
La función crece donde la derivada es positiva y la función decrece donde la función es negativa:

Crecimiento: $\bm{(-\infty,-1)\cup (-1,0)}$

Decrecimiento: $\bm{(0,1)\cup (1,+\infty)}$

La función pasa de ser creciente a ser decreciente en x=0, así que x=0 es un máximo local de la función.

Sustituimos el extremo encontrado en la función original para hallar la coordenada Y del punto:

$f(0)=\cfrac{0^2+2}{0^2-1}= \cfrac{2}{-1} = -2 \ \longrightarrow \ (0,-2)$

Así que los extremos relativos de la función son:

Máximo en el punto $\bm{(0,-2)}$

Para estudiar la curvatura de la función, calculamos su segunda derivada:

$f'(x)=\cfrac{-6x}{\left(x^2-1 \right)^2} \ \longrightarrow$ $f''(x)= \cfrac{-6 \cdot \left(x^2-1 \right)^2 - (-6x) \cdot 2(x^2-1) \cdot 2x}{ \left(\left(x^2-1 \right)^2\right)^2}$

$f''(x)= \cfrac{-6 \left(x^2-1 \right)^2 -(-6x)\cdot 4x(x^2-1)}{\left(x^2 -1\right)^4} =$ $\cfrac{-6 \left(x^2-1 \right)^2 + 24x^2(x^2-1)}{\left(x^2 -1\right)^4}$

Todos los términos tienen $(x^2-1)$ , por lo que podemos simplificar la fracción:

$f''(x)= \cfrac{-6 \left(x^2-1 \right)^{\cancel{2}} + 24x^2\cancel{(x^2-1)}}{\left(x^2-1 \right)^\cancelto{3}{4}} =\cfrac{-6 \left(x^2-1 \right) + 24x^2}{\left(x^2 -1\right)^3}$

$f''(x)= \cfrac{-6x^2+6 + 24x^2}{\left(x^2 -1\right)^3} =\cfrac{18x^2+6}{\left(x^2 -1\right)^3}$

Ahora igualamos la segunda derivada a 0 y resolvemos la ecuación:

$f''(x)= 0$

$\cfrac{18x^2+6}{\left(x^2 -1\right)^3}=0$

$18x^2+6=0\cdot \left(x^2 -1\right)^3$

$18x^2+6= 0$

$18x^2=-6$

$x^2=\cfrac{-6}{18}$

$x^2=-0,33$

$x=\sqrt{-0,33} \quad \color{red}\bm{\times}$

No existe la raíz cuadrada de un número negativo. Por lo tanto, no hay ningún punto que cumpla $f''(x)=0$

Ahora representamos en la recta todos los puntos singulares encontrados, es decir, los puntos que no pertenecen al dominio (x=-1 y x=+1) y los que anulan la segunda derivada (en este caso no hay):

Y evaluamos el signo de la segunda derivada en cada intervalo, para saber si la función es cóncava o convexa. De manera que cogemos un punto de dentro de cada intervalo (nunca los puntos singulares) y miramos qué signo tiene la segunda derivada en ese punto:

$f''(-2)=\cfrac{18(-2)^2+6}{\left((-2)^2 -1\right)^3}= \cfrac{78}{27} = 2,89 \ \rightarrow \ \bm{+}$

$f''(0)=\cfrac{18\cdot 0^2+6}{\left(0^2 -1\right)^3}= \cfrac{6}{-1} = -6 \ \rightarrow \ \bm{-}$

$f''(2)=\cfrac{18\cdot 2^2+6}{\left(2^2 -1\right)^3}= \cfrac{78}{27} = 2,89 \ \rightarrow \ \bm{+}$

Convexa $(\bm{\cup})$ : $\bm{(-\infty, -1) \cup (1, +\infty)}$

Cóncava $(\bm{\cap})$ : $\bm{(-1,1)}$

Sin embargo, aunque haya un cambio de curvatura en x=-1 y en x=1, estos no son puntos de inflexión. Porque no pertenecen al dominio de la función.

Y, finalmente, graficamos la función utilizando todos los cálculos hechos:

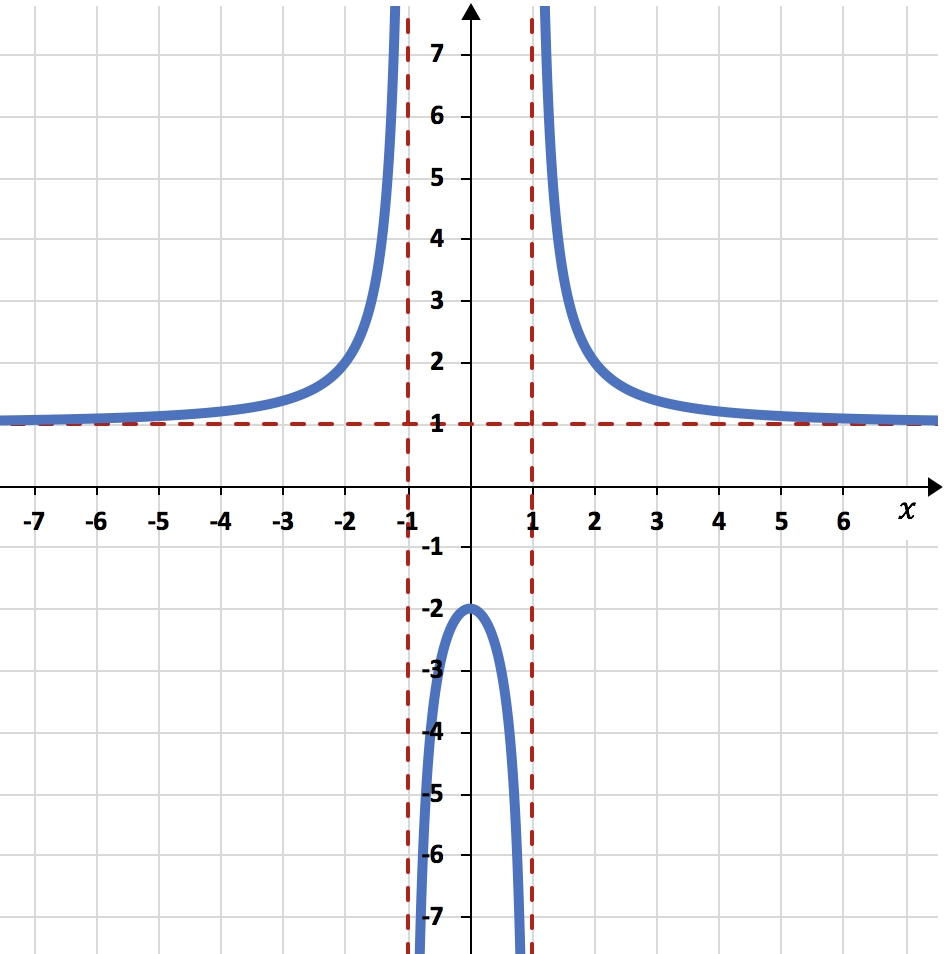
Ejercicio 3

Representa en una gráfica la siguiente función racional:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Ver solución

Se trata de una función racional, por tanto, tenemos que igualar a 0 el denominador para ver qué números no pertenecen al dominio de la función:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

Para hallar el punto de corte con el eje X, resolvemos $f(x)= 0.$ Ya que la función siempre vale 0 en el eje X:

$f(x)=0$

$\cfrac{x^3}{x^2-4}=0$

$x^3=0\cdot (x^2-4)$

$x^3=0$

$x=\sqrt[3]{0}=0$

Por tanto, el punto de corte con el eje X es:

$\bm{(0,0)}$

Y para hallar el punto de corte con el eje Y, calculamos $f(0).$ Ya que x siempre vale 0 en el eje Y:

$f(0)=\cfrac{0^3}{0^2-4} = \cfrac{0}{-4} = 0$

Por tanto, el punto de corte con el eje Y es:

$\bm{(0,0)}$

En este caso el punto de corte con el eje X coincide con el punto de corte con el eje Y, ya que la función pasas por el origen de coordenadas.

Para ver si la función tiene alguna asíntota vertical, tenemos que calcular el límite de la función en los puntos que no pertenecen al dominio (en este caso x=-2 y x=+2). Y si el resultado es infinito, se trata de una asíntota vertical. Por tanto:

$\displaystyle \lim_{x \to -2} \cfrac{x^3}{x^2-4} = \cfrac{(-2)^3}{(-2)^2-4} =\cfrac{-8}{4-4}= \cfrac{-8}{0} = \infty$

Como el límite de la función cuando x tiende a -2 da infinito, x=-2 es una asíntota vertical.

Calculamos los límites laterales de la asíntota x=-2 sustituyendo en la función un número que se le acerque mucho:

$\displaystyle f(-2,1)=\cfrac{(-2,1)^3}{(-2,1)^2-4} =-22,59 \longrightarrow \lim_{x \to -2^{-}} \cfrac{x^3}{x^2-4} = -\infty$

$\displaystyle f(-1,9)=\cfrac{(-1,9)^3}{(-1,9)^2-4} =+17,59 \longrightarrow \lim_{x \to -2^{+}} \cfrac{x^3}{x^2-4} = +\infty$

Miramos ahora si x=+2 es una asíntota vertical:

$\displaystyle \lim_{x \to +2} \cfrac{x^3}{x^2-4} = \cfrac{(2)^3}{(2)^2-4} =\cfrac{8}{4-4}= \cfrac{8}{0} = \infty$

Como el límite de la función cuando x tiende a +2 da infinito, x=+2 es una asíntota vertical.

Calculamos los límites laterales de la asíntota x=2 sustituyendo en la función un número que se le acerque mucho:

$\displaystyle f(1,9)=\cfrac{1,9^3}{1,9^2-4} =-17,59 \longrightarrow \lim_{x \to 2^{-}} \cfrac{x^3}{x^2-4} = -\infty$

$\displaystyle f(2,1)=\cfrac{2,1^3}{2,1^2-4} =22,59 \longrightarrow \lim_{x \to 2^{+}} \cfrac{x^3}{x^2-4} = +\infty$

Por otro lado, la asíntota horizontal de la función será el resultado del límite al infinito de la función. Por tanto:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^3}{x^2-4} = \cfrac{+\infty}{+\infty } =+\infty$

El límite al infinito de la función nos ha dado +∞, por tanto, la función no tiene asíntota horizontal.

Ahora calculamos la asíntota oblicua. Las asíntotas oblicuas son de la forma $y=mx+n.$ Y $m$ se calcula con la siguiente fórmula:

$\displaystyle m = \lim_{x \to +\infty} f(x):x = \lim_{x \to +\infty} \cfrac{x^3}{x^2-4}: x =\lim_{x \to +\infty} \cfrac{x^3}{x^2-4}: \frac{x}{1}$

$\displaystyle m =\lim_{x \to +\infty}\cfrac{x^3\cdot 1}{(x^2-4)\cdot x} =\lim_{x \to +\infty}\cfrac{x^3}{x^3-4x}$

$\displaystyle m =\lim_{x \to +\infty}\cfrac{x^3}{x^3-4x} = \frac{+\infty}{+\infty} = \frac{1}{1} = \bm{1}$

Una vez sabemos la pendiente de la asíntota oblicua, determinamos la ordenada en el origen utilizando la siguiente fórmula:

$\displaystyle n = \lim_{x \to +\infty} \left[f(x)-mx\right] = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-1x\right]$

$\displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}$

Pero obtenemos la indeterminación ∞ – ∞. Por tanto, tenemos que reducir los términos a común denominador. Para ello, multiplicamos y dividimos la x por el denominador de la fracción:

$\displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x \cdot (x^2-4)}{(x^2-4)}\right] =\lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x^3-4x}{x^2-4}\right]$

$\displaystyle n = \lim_{x \to +\infty} \cfrac{x^3- (x^3-4x)}{x^2-4} = \lim_{x \to +\infty} \cfrac{4x}{x^2-4}$

$\displaystyle n =\lim_{x \to +\infty} \cfrac{4x}{x^2-4} = \cfrac{+\infty}{\infty} =\bm{0}$

En defnitiva, la asíntota oblicua es:

$y = mx+n$

$y = 1x + 0$

$\bm{y = x }$

Para estudiar la monotonía de la función, primero debemos calcular su derivada:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

Ahora igualamos la derivada a 0 y resolvemos la ecuación:

$f'(x)= 0$

$\cfrac{x^4-12x^2}{\left(x^2-4\right)^2}=0$

$x^4-12x^2=0\cdot \left(x^2-4\right)^2$

$x^4-12x^2=0$

$x^2(x^2-12)=0$

$\displaystyle x^2\cdot(x^2-12) =0 \longrightarrow \begin{cases} x^2 =0 \ \longrightarrow \ \bm{x=0} \\[2ex] x^2-12=0 \ \longrightarrow \ x=\sqrt{12} \ \longrightarrow \ \bm{x= \pm 3,46} \end{cases}$

Ahora representamos en la recta todos los puntos singulares encontrados, es decir, los puntos que no pertenecen al dominio (x=-2 y x=+2) y los que anulan la derivada (x=0, x=-3,46 y x=+3,46):

$f'(-4)= \cfrac{(-4)^4-12(-4)^2}{\left((-4)^2-4\right)^2} = \cfrac{64}{144} = 0,44 \ \rightarrow \ \bm{+}$

$f'(-3)= \cfrac{(-3)^4-12(-3)^2}{\left((-3)^2-4\right)^2} = \cfrac{-27}{25} = -1,08 \ \rightarrow \ \bm{-}$

$f'(-1)= \cfrac{(-1)^4-12(-1)^2}{\left((-1)^2-4\right)^2} = \cfrac{-11}{9} = -1,22 \ \rightarrow \ \bm{-}$

$f'(1)= \cfrac{1^4-12\cdot1^2}{\left(1^2-4\right)^2} = \cfrac{-11}{9} = -1,22 \ \rightarrow \ \bm{-}$

$f'(3)= \cfrac{3^4-12\cdot 3^2}{\left(3^2-4\right)^2} = \cfrac{-27}{25} = -1,08 \ \rightarrow \ \bm{-}$

$f'(4)= \cfrac{4^4-12\cdot 4^2}{\left(4^2-4\right)^2} = \cfrac{64}{144} = 0,44 \ \rightarrow \ \bm{+}$

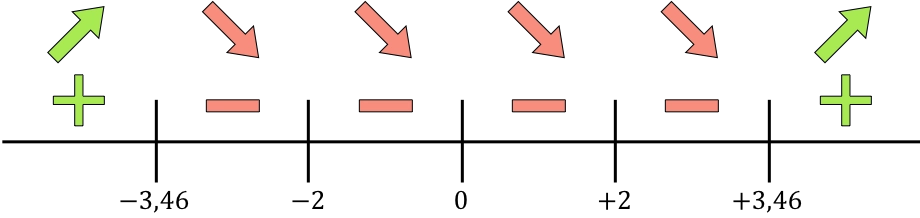
Si la derivada es positiva significa que la función crece, y si la derivada es negativa significa que la función decrece. Por tanto, los intervalos de crecimiento y decrecimiento son:

Crecimiento: $\bm{(-\infty,-3,46)\cup (3,46,+\infty)}$

Decrecimiento: $\bm{(-3,46,-2)\cup(-2,0)\cup (0,2) \cup (2,3,46)}$

La función pasa de ser creciente a ser decreciente en x=-3,46, así que x=-3,46 es un máximo de la función. Y la función pasa de ser decreciente a ser creciente en x=3,46, por lo que x=3,46 es un mínimo de la función.

Determinamos las coordenadas Y de los extemos relativos:

$f(-3,46)=\cfrac{(-3,46)^3}{(-3,46)^2-4} = \cfrac{-41,42}{7,97}=-5,20 \ \longrightarrow \ (-3,46,-5,20)$

$f(3,46)=\cfrac{3,46^3}{3,46^2-4} = \cfrac{41,42}{7,97}=5,20 \ \longrightarrow \ (3,46,5,20)$

Así que los extremos relativos de la función son:

Máximo en el punto $\bm{(-3,46,-5,20)}$

Mínimo en el punto $\bm{(3,46,5,20)}$

Para estudiar la curvatura de la función, calculamos la segunda derivada de la función:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Ahora igualamos la segunda derivada a 0 y resolvemos la ecuación:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

$x(8x^2+96)=0$

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$ no tiene solución, ya que no existe la raíz negativa de un número real.

Ahora representamos en la recta todos los puntos singulares encontrados, es decir, los puntos que no pertenecen al dominio (x=-2 y x=+2) y los que anulan la segunda derivada (x=0):

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot 1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

Convexa $(\bm{\cup})$ : $\bm{(-2,0)\cup (2,+\infty)}$

Cóncava $(\bm{\cap})$ : $\bm{(-\infty,-2)\cup (0,2)}$

Sin embargo, aunque haya un cambio de curvatura en x=-2 y en x=+2, estos no son puntos de inflexión. Porque x=-2 y x=+2 no pertenecen al dominio de la función. En cambio, en x=0 hay un cambio de curvatura (la función pasa de convexa a cóncava) y sí que pertenece a la función, por tanto, x=0 es un punto de inflexión.

Sustituimos los puntos de inflexión encontrados en la función original para hallar la otra coordenada del punto de inflexión:

$f(0) = \cfrac{0^3}{0^2-4} = \cfrac{0}{-4} =0\ \longrightarrow \ (0,0)$

Así que los puntos de inflexión de la función son:

Puntos de inflexión: $\bm{(0,0)}$

Finalmente, a partir de toda la información que hemos calculado, representamos la función:

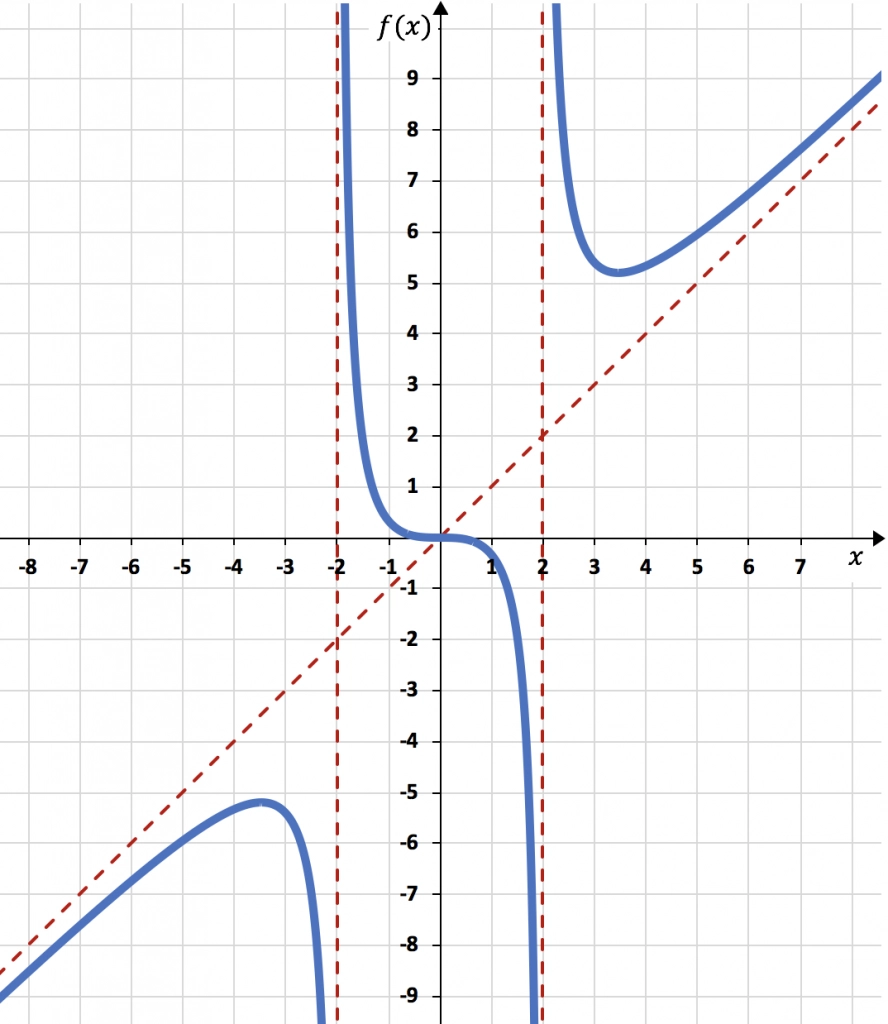
representacion grafica de funciones ejercicios resueltos

Comentario: Fíjate que la función cruza la asíntota oblicua en el punto $(0,0) .$ Eso es porque las asíntotas oblicuas determinan sobre todo el comportamiento de la función cuando x tiende a +∞ y a -∞, de hecho, la función nunca llega cruzar la asíntota oblicua en la derecha de la gráfica (x→+∞) y en la izquierda de la gráfica (x→-∞). Aún así, es muy poco frecuente que la función cruce la asíntota oblicua por el medio, se trata de un caso muy especial.

Representación de funciones

Cómo representar una función en una gráfica

Ejemplo de la representación de una función

Ejercicios resueltos de representación de funciones

Ejercicio 1

Ejercicio 2

Ejercicio 3

Deja un comentario Cancelar respuesta