Funciones logarítmicas

En esta página encontrarás qué son las funciones logarítmicas y también cómo representarlas en una gráfica. Además, verás todas sus características, cómo calcular su dominio y varios ejemplos para entenderlo mejor. Finalmente, podrás practicar con ejercicios y problemas resueltos paso a paso de funciones logarítmicas.

¿Qué es una función logarítmica?

La definición de una función logarítmica es la siguiente:

En matemáticas, las funciones logarítmicas son aquellas funciones cuya variable independiente x forma parte del argumento de un logaritmo. Es decir, son de la siguiente forma:

f(x)=\log_a x

Donde a es obligatoriamente un número real positivo y diferente de 1.

Por ejemplo, la siguiente función es logarítmica:

f(x)=\log_5 x

Antes de ver las características de las funciones logarítmicas, vamos a repasar brevemente el concepto de logaritmo:

  • El logaritmo en base a de y es el elemento al que hay elevar el número a para que dé como resultado el número y.

\log_a y = x \iff a^x = y

Recuerda también que el logaritmo neperiano (o logaritmo natural) es equivalente al logaritmo cuya base es el número exponencial e:

\ln x = \log_e x

Por otro lado, se suele omitir la base cuando esta es 10. Este tipo de logaritmos se llaman logaritmos decimales o algoritmos comunes:

\log_{10} x = \log x

Dominio de una función logarítmica

Un logaritmo solo admite números positivos, por lo tanto, el dominio de una función logarítmica serán todos los números que satisfagan esta condición.

A modo de ejemplo, vamos a calcular el dominio de la siguiente función logarítmica:

f(x)=\log_3 (2x-4)

El argumento de un logaritmo tiene que ser más grande que 0, ya que no existen ni los logaritmos de números negativos ni el logaritmo de 0. Así que tenemos que mirar cuándo el argumento de la función es mayor que cero:

2x-4>0

Ahora resolvemos la inecuación:

2x>4

x>\cfrac{4}{2}

x>2

De modo que el argumento del logaritmo será más grande que cero si x es mayor que 2. Así que el dominio de la función son todos los números más grandes que 2 (no incluido):

\text{Dom } f = (2,+\infty)

Características de las funciones logarítmicas

  • Como hemos visto, el dominio de una función logarítmica son todas las x que hacen que el argumento del logaritmo sea positivo.
  • El recorrido o rango de una función logarítmica son todos los números reales.

\text{Im } f= \mathbb{R}

  • Toda función logarítmica es una función continua e inyectiva.
  • El crecimiento o decrecimiento de una función logarítmica depende de la base del logaritmo: si la base es mayor que 1 (a>1) la función es creciente, en cambio, si la base está dentro del intervalo entre cero y uno (0<a<1) la función es decreciente.
  • Del mismo modo, la curvatura de cualquier función logarítmica también viene definida por su base: la función será cóncava (en forma de \bm{\cap}) si la base es superior a 1, por contra, será convexa (en forma de \bm{\cup}) si la base es menor que 1.
  • La inversa de la función logarítmica es la función exponencial. Por tanto, las gráficas de una función logarítmica y una función exponencial son simétricas respecto de la recta y=x si ambas poseen la misma base.

Cómo representar una función logarítmica en una gráfica

A continuación vamos a ver con un ejemplo cómo graficar una función logarítmica.

  • Representa en un gráfico la siguiente función:

f(x)=\log_2 (x-1)

Lo primero que debemos hacer es hallar el dominio de la función. Y, como es un logaritmo, su argumento tiene que ser más grande que 0, ya que no existen ni los logaritmos de números negativos ni el logaritmo de 0. Así que miramos cuándo el argumento de \log_2 (x-1) es mayor que 0:

x-1>0

x>1

Por tanto, el argumento del logaritmo será positivo si y solo si x es mayor que 1. De manera que el dominio de la función son todos los números más grandes que 1 (no incluido):

\text{Dom } f = (1,+\infty)

Una vez sabemos el dominio de la función logarítmica, creamos una tabla de valores. Evidentemente, cuantos más puntos se calculen, más exacta será la representación de la función. Pero calculando unos 5 puntos dentro del intervalo del dominio es suficiente:

  • x= 1,5 \ \longrightarrow \ f(1,5)=\log_2 (1,5-1)=-1
  • x= 2 \ \longrightarrow \ f(2)=\log_2 (2-1)= 0
  • x= 3 \ \longrightarrow \ f(3)=\log_2 (3-1) = 1
  • x= 5 \ \longrightarrow \ f(5)=\log_2 (5-1) = 2
  • x= 9 \ \longrightarrow \ f(9)=\log_2 (9-1) = 3

\begin{array}{c|c} x & f(x) \\ \hline 1,5 & -1 \\ 2 & 0 \\ 3 & 1 \\ 5 & 2 \\ 9 & 3 \end{array}

Te recomendamos usar la calculadora para encontrar los puntos de la tabla de valores, ya que no son fáciles de calcular a mano. Sin embargo, en algunas calculadoras solo se pueden calcular los logaritmos de base 10, en tal caso recuerda que puedes hallar el resultado de cualquier logaritmo aplicando la propiedad de cambio de base de los logaritmos:

\log_2 0,5 = \cfrac{ \log 0,5 }{ \log 2} = -1

Ahora representamos los puntos obtenidos en un gráfico:

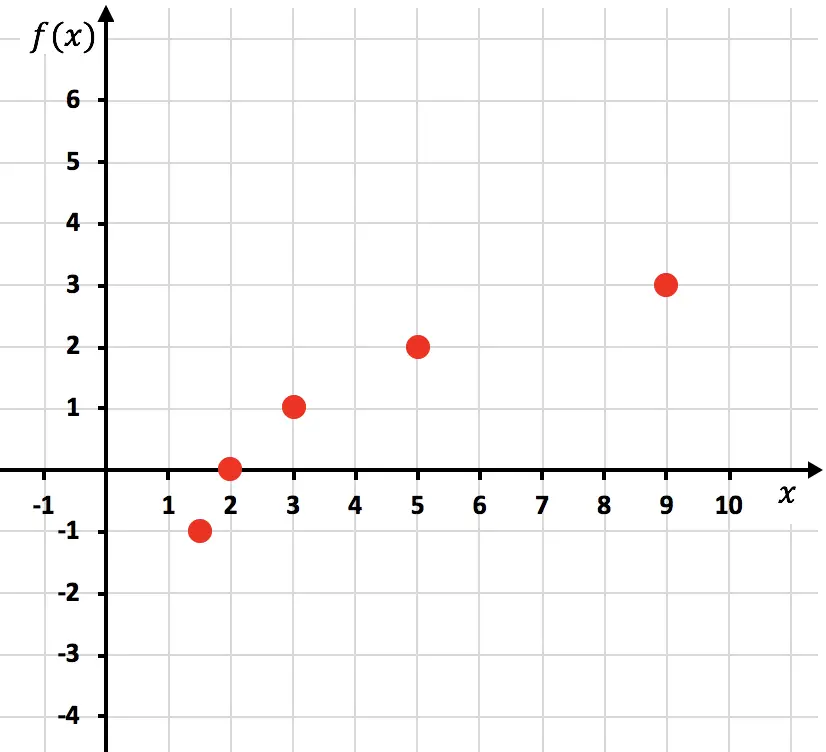
Y finalmente unimos los puntos y alargamos la función:

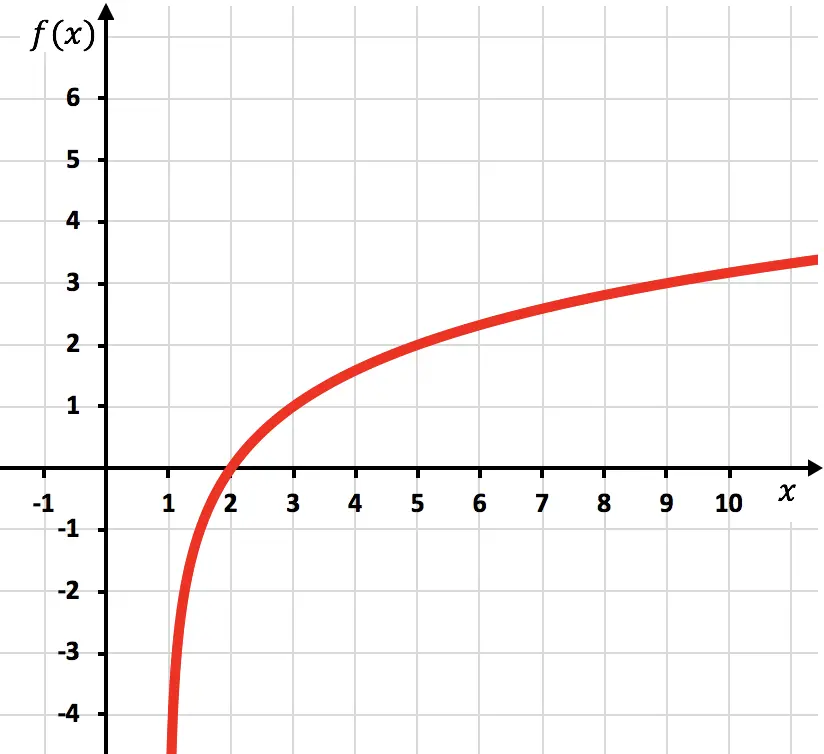
ejemplo de representacion grafica de una funcion logaritmica

Fíjate que la función por la derecha sigue creciendo hasta el infinito. En cambio, la función por la izquierda va decreciendo pero nunca llega a tocar x=1. Aunque se acerca mucho, nunca lo llega a tocar. Eso significa que la recta x=1 es una asíntota vertical de la función.

Ejercicios resueltos de funciones logarítmica

Ejercicio 1

Calcula el dominio de la siguiente función logarítmica:

f(x)= \log_8 4x

No existe ni el logaritmo de un número negativo ni el logaritmo de 0. Por tanto, debemos mirar cuándo el argumento del logaritmo es más grande que 0:

4x>0

x>\cfrac{0}{4}

x>0

\mathbf{Dom } \ \bm{f = (0,+\infty)}

 

Ejercicio 2

Halla el dominio de la siguiente función logarítmica:

f(x)= \log (4-x)

No existe ni el logaritmo de un número negativo ni el logaritmo de 0. Por tanto, debemos mirar cuándo el argumento del logaritmo es mayor que cero:

4-x>0

-x>-4

x<\cfrac{-4}{-1} = 4

Recuerda que si en una inecuación cambiamos de lado un número negativo que está multiplicando o dividiendo también hay que girar el signo de la inecuación.

x<4

\mathbf{Dom } \ \bm{f = (-\infty,4)}

 

Ejercicio 3

Representa en una gráfica la siguiente función logarítmica:

f(x)= \log_2 x

En primer lugar, tenemos que calcular el dominio de la función logarítmica:

x>0

\text{Dom } f = (0,+\infty)

Ahora creamos una tabla de valores otorgando valores a x dentro del intervalo del dominio:

x= 0,5 \ \longrightarrow \ f(0,5)= \log_2 0,5= -1

x= 1 \ \longrightarrow \ f(1)= \log_2 1= 0

x= 2 \ \longrightarrow \ f(2)= \log_2 2= 1

x= 4 \ \longrightarrow \ f(4)= \log_2 4= 2

x= 8 \ \longrightarrow \ f(8)= \log_2 8= 3

\begin{array}{c|c} x & f(x) \\ \hline 0,5 & -1 \\ 1 & 0 \\ 2 & 1 \\ 4 & 2 \\ 8 & 3 \end{array}

Por último, representamos los puntos en la gráfica y dibujamos la función:

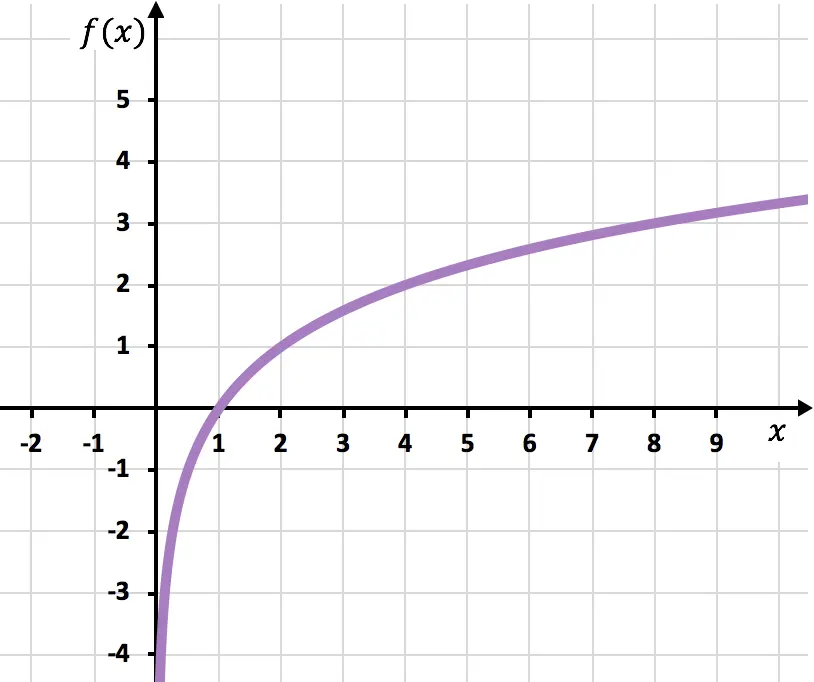
ejercicios resueltos de funciones logaritmicas

Fíjate que la función por la derecha sigue creciendo hasta el infinito. En cambio, por la izquierda la función va decreciendo pero nunca llega a cruzar x=0. Eso es porque la función tiene una asíntota vertical en el eje Y.

 

Ejercicio 4

Representa gráficamente la siguiente función logarítmica:

f(x)= \log_2 (x+2)

Lo primero que debemos hacer es calcular el dominio de la función logarítmica:

x+2>0

x>-2

\text{Dom } f = (-2,+\infty)

Ahora creamos una tabla de valores dando valores a x dentro del intervalo del dominio:

x= -1,5 \ \longrightarrow \ f(-1,5)= \log_2 (-1,5+2)= -1

x= -1 \ \longrightarrow \ f(-1)= \log_2 (-1+2)=0

x= 0 \ \longrightarrow \ f(0)=\log_2 (0+2)=1

x= 2 \ \longrightarrow \ f(2)=\log_2 (2+2)=2

x= 6 \ \longrightarrow \ f(6)=\log_2 (6+2)=3

\begin{array}{c|c} x & f(x) \\ \hline -1,5 & -1 \\ -1 & 0 \\ 0 & 1 \\ 2 & 2 \\ 6 & 3 \end{array}

Finalmente, representamos los puntos en la gráfica y trazamos la función:

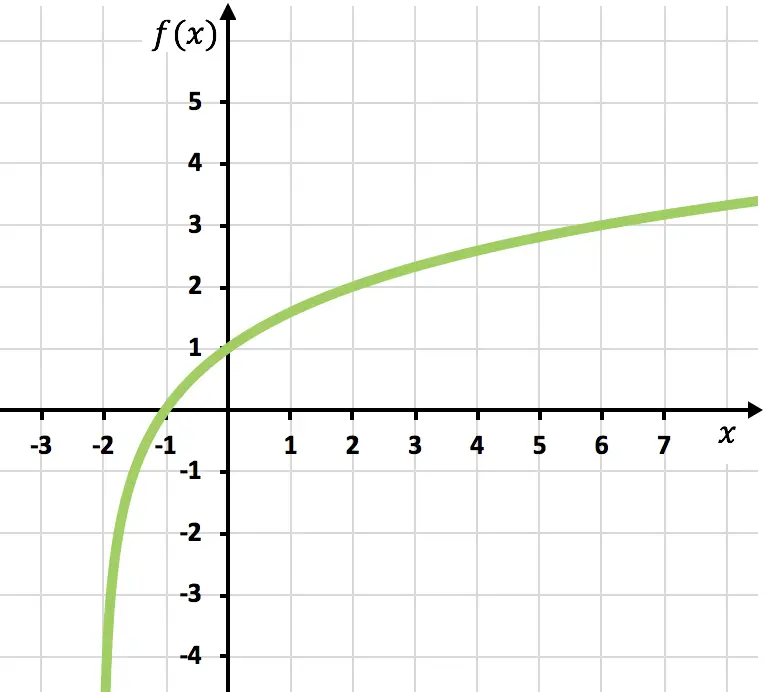
ejercicio resuelto paso a paso de funcion logaritmica

Fíjate que la función por la derecha sigue creciendo hasta el infinito. En cambio, por la izquierda la función va disminuyendo pero nunca llega a cruzar x=-2. Eso es porque tiene una asíntota vertical en x=-2.

 

Ejercicio 5

Realiza la representación gráfica de la siguiente función logarítmica:

f(x)=\log_3 x

Lo primero que debemos hacer es calcular el dominio de la función logarítmica:

x>0

\text{Dom } f = (0,+\infty)

Ahora creamos una tabla de valores evaluando la función en varios puntos de dentro del intervalo del dominio:

x= 1 \ \longrightarrow \ f (1)= \log_3 1= 0

x= 3 \ \longrightarrow \ f(3)= \log_3 3= 1

x= 9 \ \longrightarrow \ f(9)= \log_3 9= 2

\displaystyle x= \cfrac{1}{3} \ \longrightarrow \ f\left( \frac{1}{3} \right)= \log_3 \frac{1}{3}= -1

\displaystyle x= \cfrac{1}{9} \ \longrightarrow \ f\left( \frac{1}{9} \right)= \log_3 \frac{1}{9}= -2

\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 3 & 1 \\ 9 & 2 \\ \frac{1}{3} & -1 \\[1.1ex] \frac{1}{9} & -2 \end{array}

Y, para acabar, representamos los puntos en la gráfica y pintamos la función:

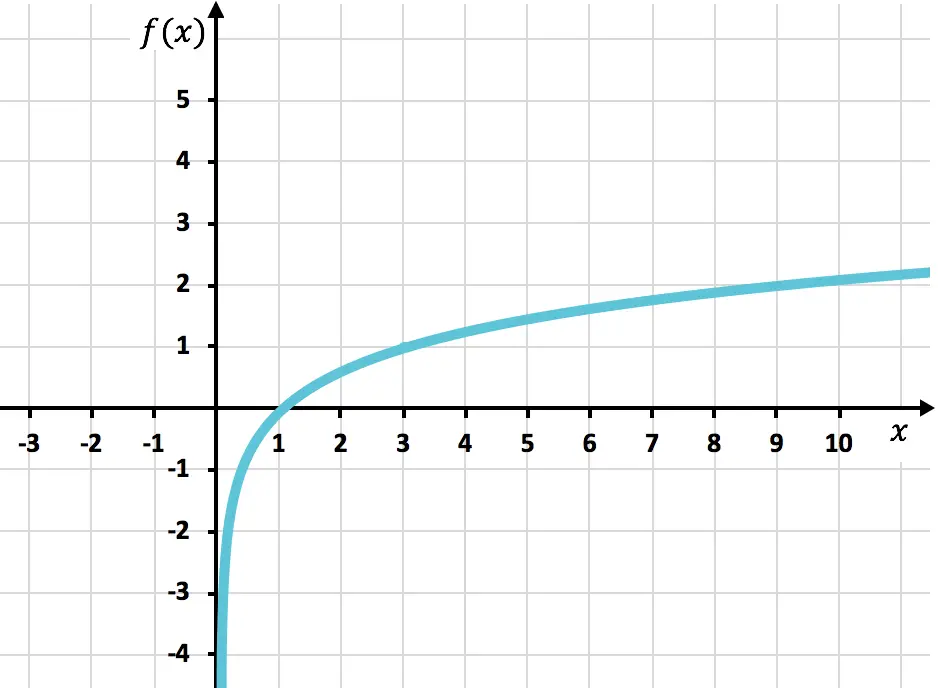
ejemplos de funciones logaritmicas o con logaritmos

Fíjate que la función por la derecha sigue creciendo hasta el infinito. Pero por la izquierda la función va disminuyendo aunque nunca llega a cruzar x=0. Eso es debido a que la función tiene una asíntota vertical en el eje de las ordenadas.

 

Ejercicio 6

Representa en un gráfico la siguiente función con logaritmo:

f(x)= \log_2 (1-x)

Antes de graficar la función, debemos calcular su dominio:

1-x>0

-x>-1

x<\cfrac{-1}{-1} = 1

Recuerda que si en una inecuación cambiamos de lado un número negativo que está multiplicando o dividiendo también hay que invertir el signo de la inecuación

x<1

\text{Dom } f = (-\infty,1)

Ahora creamos una tabla de valores dando valores a x dentro del intervalo del dominio:

x= 0,5 \ \longrightarrow \ f(0,5)= \log_2 (1-0,5)=-1

x= 0 \ \longrightarrow \ f(0)= \log_2 (1-0)= 0

x= -1 \ \longrightarrow \ f(-1)=\log_2 (1-(-1))=1

x= -3 \ \longrightarrow \ f(-3)=\log_2 (1-(-3))=2

x= -7 \ \longrightarrow \ f(-7)=\log_2 (1-(-7))=3

\begin{array}{c|c} x & f(x) \\ \hline 0,5 & -1 \\ 0 & 0 \\ -1 & 1 \\ -3 & 2 \\ -7 & 3 \end{array}

Y, para finalizar, representamos los puntos en la gráfica y trazamos la función:

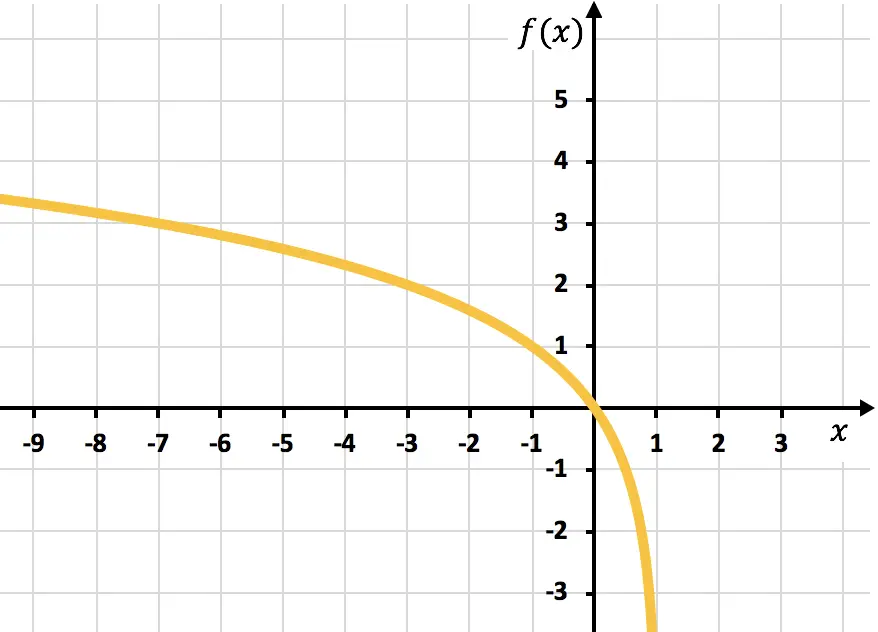
funcion logaritmica dominio

Fíjate que la función por la izquierda sigue creciendo hasta el infinito. En cambio, por la derecha la función va disminuyendo pero nunca llega a cruzar x=1. Por lo tanto, tiene una asíntota vertical en la recta x=1.

 

Propiedades de los logaritmos

A modo de repaso, a continuación tienes las propiedades de los logaritmos por si necesitas hacer operaciones con funciones logarítmicas:

  • El logaritmo de un producto es equivalente a la suma de los logaritmos de los factores.

\log(A\cdot B) = \log A + \log B

  • El logaritmo de un cociente es igual a la diferencia del logaritmo del dividendo menos el logaritmo del divisor.

\displaystyle \log \left(\frac{A}{B} \right) = \log A - \log B

  • El logaritmo de una potencia es lo mismo que multiplicar el exponente de la potencia por el logaritmo de la base.

\displaystyle \log A^n = n\cdot \log A

  • El logaritmo de una raíz es igual a dividir el logaritmo del radicando entre el índice de la raíz.

\displaystyle \log \sqrt[n]{A} =\cfrac{\log A}{n}

2 comentarios en “Funciones logarítmicas”

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *