Función exponencial

En esta página encontrarás qué son las funciones exponenciales y también cómo representar en un gráfico una función exponencial. Además, verás todas sus características y varios ejemplos para entenderlo perfectamente. Finalmente, podrás practicar con ejercicios y problemas resueltos paso a paso sobre funciones exponenciales.

¿Qué es una función exponencial?

La definición de función exponencial es la siguiente:

En matemáticas, las funciones exponenciales son aquellas funciones que tienen la variable independiente x en el exponente de una potencia. Es decir, son de la siguiente forma:

f(x)=a^x

Donde a es un número real positivo y diferente de 1.

Ejemplos de funciones exponenciales

Las siguientes funciones son ejemplos de funciones exponenciales:

f(x)=3^{x}

f(x)=4^{-x}

\displaystyle f(x)=\left( \frac{1}{2} \right)^x

f(x)=5^x

Características de las funciones exponenciales

Las funciones exponenciales tienen las siguientes propiedades:

  • El dominio de una función exponencial son todos los números reales, o dicho con otras palabras, una función exponencial existe por cualquier valor de x.

\text{Dom } f=\mathbff{R}

  • Sin embargo, la función solo toma valores positivos, por lo tanto, el recorrido o rango de una función exponencial son todos los números reales positivos.

\text{Im } f= (0,+\infty)

  • Toda función exponencial es una función continua e inyectiva a la vez.
  • Si la función no está trasladada, cualquier función exponencial pasa por el punto (0,1). Porque la función evaluada en el cero siempre da como resultado uno.

f(0)=a^0=1

  • Asimismo, el valor de una función exponencial en x=1 es igual a la base.

f(1)=a^1=a

  • Si la base de la potencia (a) es mayor que 1 la función exponencial es creciente. Por contra, si el coeficiente a está dentro del intervalo entre 0 y 1 la función exponencial es decreciente.
  • En general, el eje X es una asíntota horizontal de una función exponencial.
  • La inversa de la función exponencial es la función logarítmica. Por tanto, las gráficas de una función exponencial y una función logarítmica son simétricas respecto de la recta y=x si ambas poseen la misma base.

Cómo representar en una gráfica una función exponencial

Las funciones exponenciales son muy sencillas de representar. Así que vamos a ver cómo graficar una función exponencial en un gráfico mediante un ejemplo.

  • Representa en una gráfica la siguiente función exponencial:

f(x)=2^x

En las funciones exponenciales no hace falta calcular el dominio, porque siempre serán todos los números reales:

\text{Dom } f = \mathbb{R}

Por tanto, simplemente tenemos que hacer la tabla de valores. Como este tipo de funciones cambian mucho de un punto a otro, calcularemos 5 puntos. Pero cuantos más puntos calculemos, más precisa será la representación de la función. 

  • x= 0 \ \longrightarrow \ f(0)=2^0= 1
  • x= 1 \ \longrightarrow \ f(1)=2^1= 2
  • x= 2 \ \longrightarrow \ f(2)=2^2= 4
  • x= -1 \ \longrightarrow \ f(-1)=2^{-1}= 0,5
  • x= -2 \ \longrightarrow \ f(-2)=2^{-2}= 0,25

\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 4 \\ -1 & 0,5 \\ -2 & 0,25 \end{array}

Te recomendamos usar la calculadora para hallar los puntos de la tabla de valores, ya que son complicados de calcular a mano.

Ahora representamos los puntos en un gráfico:

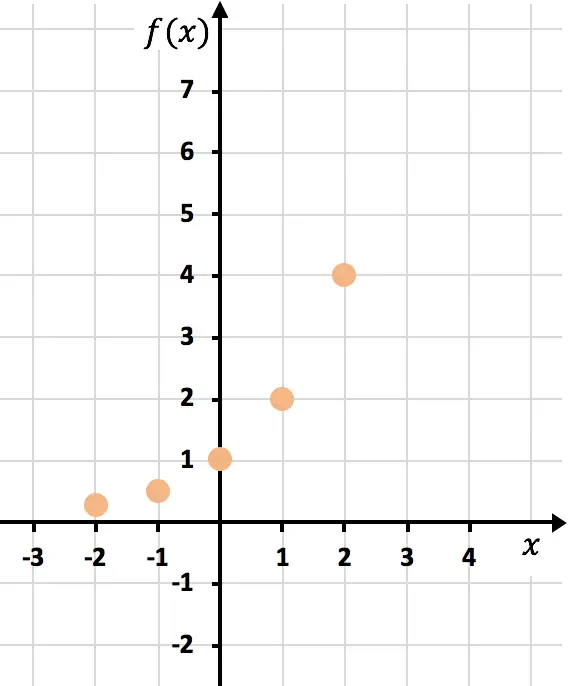
Y finalmente unimos los puntos y alargamos la función:

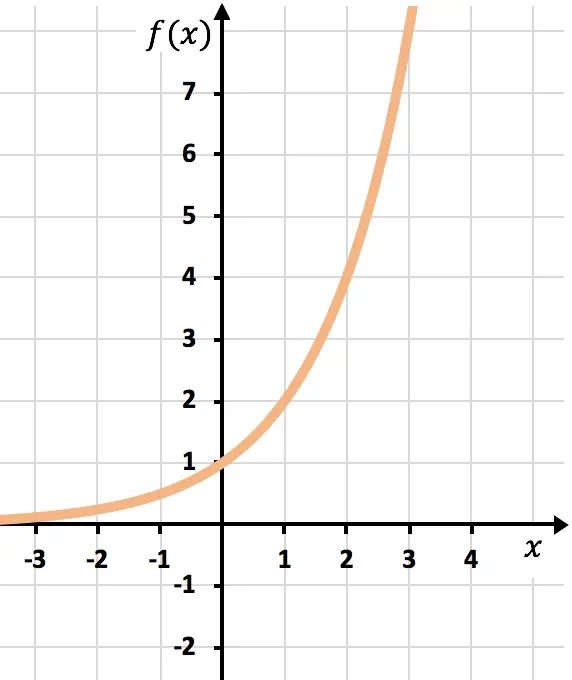
como representar o graficar una funcion exponencial

Fíjate que la función por la derecha sigue creciendo hasta el infinito.

En cambio, la función por la izquierda va decreciendo pero nunca llega a 0. Aunque se acerca mucho, nunca lo llega a tocar. Eso quiere decir que la recta y=0 (el eje de las abscisas) es una asíntota horizontal.

Ejercicios resueltos de funciones exponenciales

Ejercicio 1

Representa gráficamente la siguiente función exponencial:

f(x)= 2^x+1

Se trata de una función exponencial, por lo tanto, para representarla tenemos que crear una tabla de valores otorgando valores a la variable x:

x= 0 \ \longrightarrow \ f(0)= 2^0+1=2

x= 1 \ \longrightarrow \ f(1)= 2^1+1=3

x= 2 \ \longrightarrow \ f(2)= 2^2+1=5

x= -1 \ \longrightarrow \ f(-1)= 2^{-1}+1=1,5

x= -2 \ \longrightarrow \ f(-2)= 2^{-2}+1=1,25

\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 3 \\ 2 & 5 \\ -1 & 1,5 \\ -2 & 1,25 \end{array}

Una vez tenemos la tabla de valores, representamos los puntos obtenidos en la gráfica y trazamos la función:

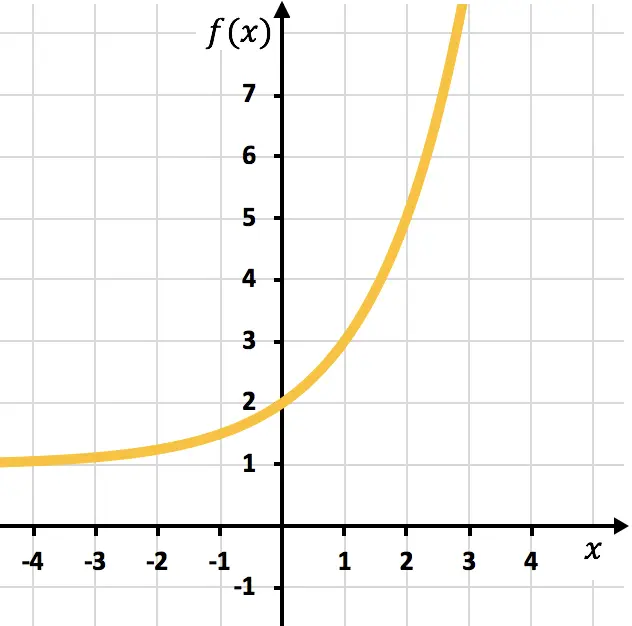
ejercicio resuelto paso a paso de funciones exponenciales

Fíjate que la función por la derecha sigue creciendo hasta el infinito. En cambio, por la izquierda la función va disminuyendo pero nunca llega a cruzar el 1. Eso es porque la función tiene una asíntota horizontal en la recta y=1.

En este caso la asíntota horizontal está en y=1 en vez del eje OX porque se ha hecho a la función una traslación vertical de una unidad hacia arriba.

 

Ejercicio 2

Representa en una gráfica la siguiente función exponencial:

\displaystyle f(x)= \left(\frac{1}{3}\right)^x

Se trata de una función exponencial, de modo que para graficarla tenemos que construir una tabla de valores otorgando valores a la variable x:

x= 0 \ \longrightarrow \ f(0)= \left(\cfrac{1}{3}\right)^0 = 1

x= 1 \ \longrightarrow \ f(1)= \left(\cfrac{1}{3}\right)^1 = 0,33

x= 2 \ \longrightarrow \ f(2)= \left(\cfrac{1}{3}\right)^2 = 0,11

x= -1 \ \longrightarrow \ f(-1)= \left(\cfrac{1}{3}\right)^{-1} = 3

x= -2 \ \longrightarrow \ f(-2)= \left(\cfrac{1}{3}\right)^{-2} = 9

\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 0,33 \\ 2 & 0,11 \\ -1 & 3 \\ -2 & 9 \end{array}

Una vez tenemos la tabla de valores, representamos los puntos calculados en la gráfica y dibujamos la función:

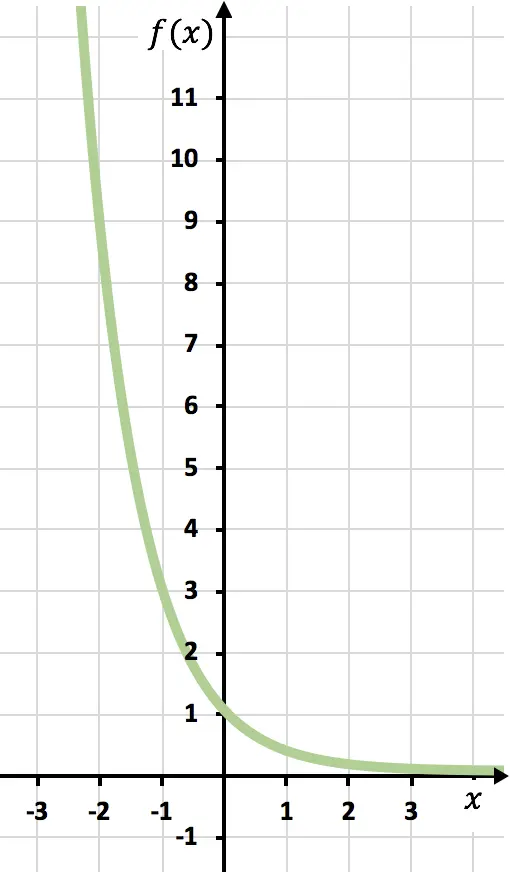
ejercicios resueltos de funciones exponenciales

Fíjate que la función por la izquierda sigue creciendo hasta el infinito. En cambio, por la derecha la función va disminuyendo pero nunca llega a cruzar el 0. Eso es porque la función tiene una asíntota horizontal en y=0 (el eje X).

 

Ejercicio 3

Representa en un gráfico la siguiente función exponencial:

\displaystyle f(x)= \left(\frac{1}{2}\right)^x+3

Se trata de una función exponencial, por lo que para dibujarla tenemos que crear una tabla de valores evaluando la función en varios puntos:

x= 0 \ \longrightarrow \ f(0)= \left(\cfrac{1}{2}\right)^0+3 = 4

x= 1 \ \longrightarrow \ f(1)= \left(\cfrac{1}{2}\right)^1+3 = 3,5

x= 2 \ \longrightarrow \ f(2)= \left(\cfrac{1}{2}\right)^2+3 = 3,25

x= -1 \ \longrightarrow \ f(-1)= \left(\cfrac{1}{2}\right)^{-1}+3 = 5

x= -2 \ \longrightarrow \ f(-2)= \left(\cfrac{1}{2}\right)^{-2}+3 = 7

\begin{array}{c|c} x & f(x) \\ \hline 0 & 4 \\ 1 & 3,5 \\ 2 & 3,25 \\ -1 & 5 \\ -2 & 7 \end{array}

Por último, representamos los puntos obtenidos en la gráfica y trazamos la función:

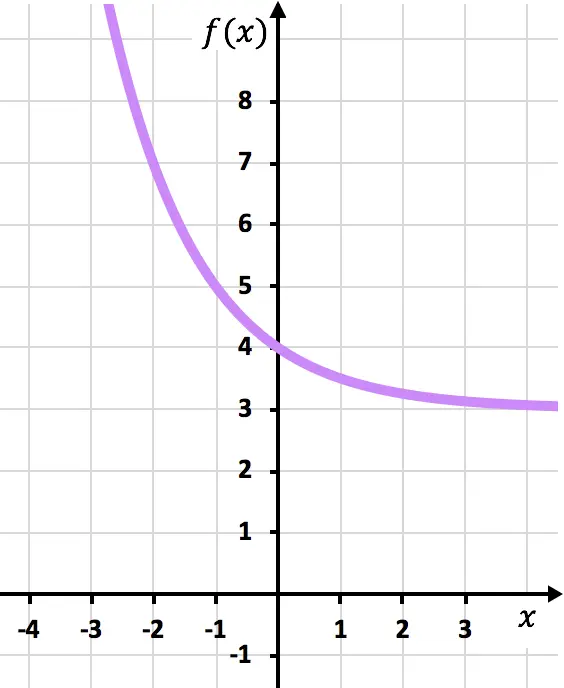
problema de funcion exponencial

Fíjate que la función por la izquierda crece ilimitadamente hasta el infinito. En cambio, por la derecha la función va decreciendo pero nunca llega a cruzar el 3. Eso es porque la función tiene una asíntota horizontal en y=3.

En este caso la asíntota horizontal está en y=3 en vez del eje X porque se ha desplazado verticalmente la función tres unidades hacia arriba.

 

Ejercicio 4

Resuelve el siguiente problema sobre las funciones exponenciales.

  • Determina el valor de k para que la siguiente función exponencial pase por el punto (2,8).

f(x)=k\cdot 2^x

La función debe pasar por el punto (2,8), por tanto, podemos sustituir los valores de x y de f(x) del punto en la función para hallar el valor de la constante k:

f(x)=k\cdot 2^x \ \xrightarrow{x \ = \ 2 \ ; \ f(x) \ = \ 8} \ 8 = k \cdot 2^2

Y ahora resolvemos la ecuación resultante:

8 = k \cdot 2^2

8 = k \cdot 4

\cfrac{8}{4} = k

\bm{ 2 = k}

 

Ejercicio 5

Resuelve el siguiente problema sobre las funciones exponenciales.

Una población de termitas se reproduce según la siguiente función:

f(t)=3^{t+1}

Donde f(t) es el número de termitas y t el tiempo transcurrido en meses.

¿Cuántas termitas habrá al cabo de 1 año?

Para calcular las termitas que habrá en un año lo único que debemos hacer es sustituir el tiempo transcurrido (1 año) en la función. Pero como en la función t son los meses transcurridos y no los años, tenemos que poner t=12 ya que en un año hay 12 meses:

f(t)=3^{t+1}

f(12)=3^{12+1}

f(12)=3^{13}

Resolvemos con la calculadora:

f(12)= 1594323

De manera que al cabo de un año habrá 1 594 323 termitas.

 

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *