En este post te explicamos cómo derivar la arcocosecante hiperbólica de una función. Asimismo, encontrarás ejemplos resueltos de la derivada de la arcocosecante hiperbólica.
Índice
Fórmula de la derivada de la arcocosecante hiperbólica
La derivada de la arcocosecante hiperbólica de x es igual a menos 1 dividido entre el producto de x por la raíz de uno más x al cuadrado.
Por lo tanto, la derivada de la arcocosecante hiperbólica de un función es menos la derivada de dicha función partido por el producto de la función por la raíz de uno más la función al cuadrado.
En resumen, la fórmula para calcular la derivada de la función arcocosecante hiperbólica es la siguiente:
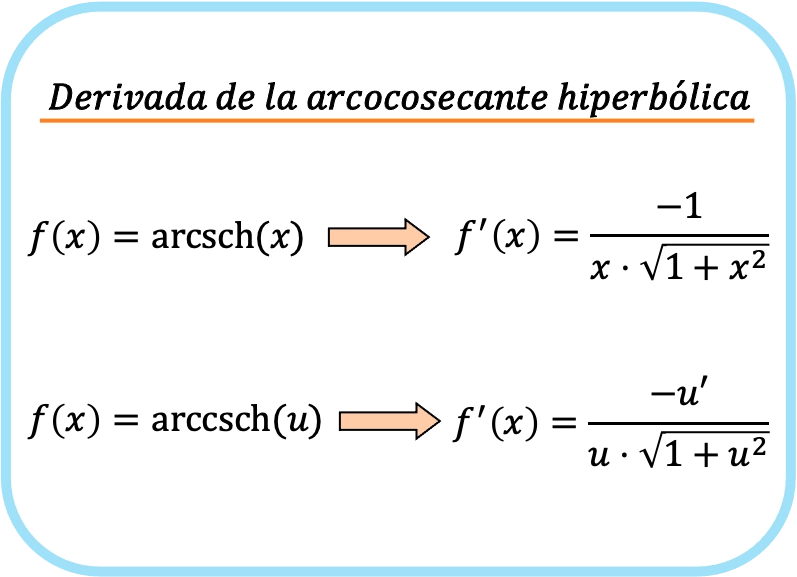
Aunque hayamos puesto dos fórmulas, no significa que sean diferentes. Si te fijas bien, la segunda fórmula es como la primera pero aplicando la regla de la cadena.
Ejemplos de la derivada de la arcocosecante hiperbólica
Vista la fórmula de la derivada de la arcocosecante hiperbólica, a continuación derivaremos dos funciones de este tipo para que veas cómo se hace.
Ejemplo 1
En este ejercicio tenemos que usar la fórmula de la derivada de la arcocosecante hiperbólica con la regla de la cadena, ya que en el argumento hay una función diferente de x:
Así pues, para hallar la derivada debemos sustituir la u por 3x y la u’ por su derivada, que es 3:
Ejemplo 2
En este caso tenemos una función polinómica en el argumento de la arcocosecante hiperbólica, por lo que también debemos usar la regla de la cadena para derivarla:
De modo que ponemos la derivada de la función del argumento en el numerador de la fracción, y en el denominador cambiamos la u por la función polinómica:

