En este post te explicamos cómo derivar la cosecante hiperbólica de una función. Además, podrás ver varios ejemplos resueltos de la derivada de la cosecante hiperbólica.
Índice
Fórmula de la derivada de la cosecante hiperbólica
La derivada de la cosecante hiperbólica de x es igual a menos la cosecante hiperbólica de x por la cotangente hiperbólica de x.
Por lo tanto, la derivada de la cosecante hiperbólica de un función es menos el producto de la cosecante hiperbólica de la función por la cotangente hiperbólica de la función por la derivada de dicha función.
En definitiva, la fórmula para derivar la cosecante de una función es la siguiente:
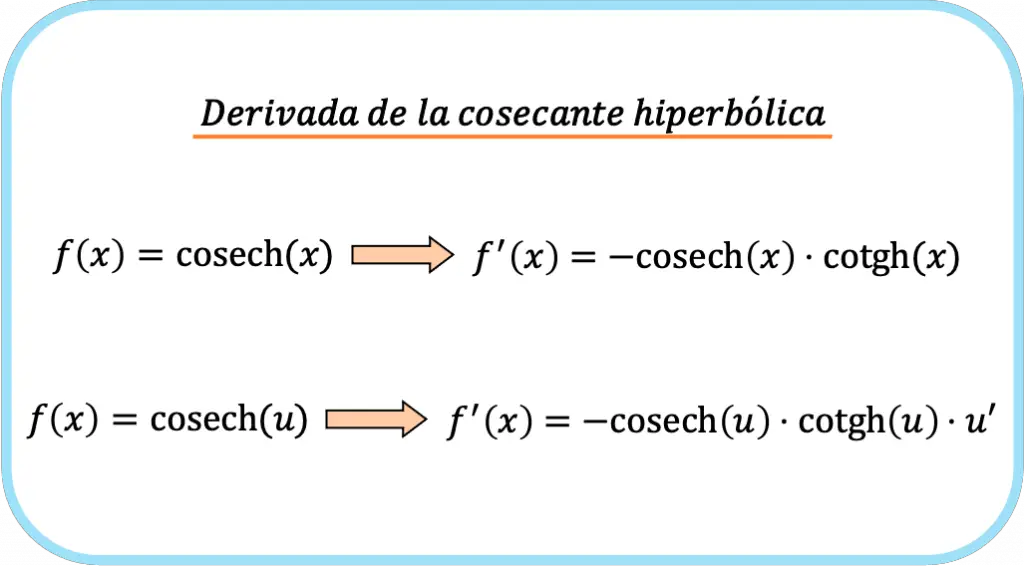
En realidad, las dos expresiones anteriores corresponden a una única fórmula, la diferencia es que en la segunda fórmula se aplica la regla de la cadena.
Ejemplos de la derivada de la cosecante hiperbólica
Después de ver cuál es la fórmula de la derivada de la cosecante hiperbólica, a continuación tienes varios ejemplos resueltos de este tipo de derivada trigonométrica.
Ejemplo 1
En este primer ejemplo derivaremos la cosecante hiperbólica de x al cuadrado:
La función del argumento de la cosecante hiperbólica es diferente de x, por lo tanto, debemos usar la fórmula de la derivada de la cosecante hiperbólica con la regla de la cadena.
Así que para derivar esta función trigonométrica simplemente tenemos que sustituir los valores en la fórmula anterior, esto es, en el argumento de la cosecante hiperbólica y de la tangente hiperbólica ponemos x2, y multiplicamos todo por la derivada de x al cuadrado, que es 2x:
Ejemplo 2
En este ejercicio veremos cuánto es la derivada de la cosecante hiperbólica de x al cubo:
Para hallar la derivada de la cosecante hiperbólica de una función, aplicamos su fórmula:
La derivada de x al cubo es 3x2, por lo que la derivada de toda la función es:

