▷ Derivada de la cosecante (fórmula y ejemplos)

En este post te explicamos cómo derivar la cosecante de una función (fórmula). También encontrarás ejercicios resueltos paso a paso de la derivada de la cosecante. Y, por último, podrás ver la demostración de la fórmula de este tipo de derivada trigonométrica.

Índice

Fórmula de la derivada de la cosecante

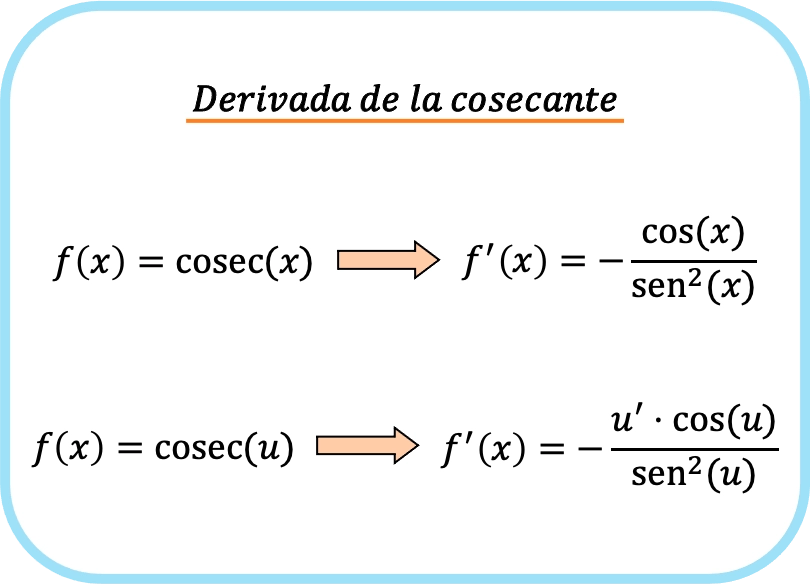
La derivada de la cosecante de x es igual a menos el cociente del coseno de x partido por el seno al cuadrado de x.

$f(x)=\text{cosec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{\text{cos}(x)}{\text{sen}^2(x)}$

Aplicando las fórmulas trigonométricas, también se puede definir la derivada de la cosecante de x como menos el producto de la cotangente de x por la cosecante de x.

$f'(x)=-\cfrac{\text{cos}(x)}{\text{sen}^2(x)}=-\cfrac{\text{cos}(x)}{\text{sen}(x)}\cdot \cfrac{1}{\text{sen}(x)}=-\text{cot}(x)\cdot \text{cosec}(x)$

Y si aplicamos la regla de la cadena, la derivada de la cosecante de un función es menos el producto de la derivada de la función por el coseno de la función, dividido entre el seno al cuadrado de la función.

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

De modo que la fórmula que sirve para derivar la cosecante de una función es la siguiente:

Ejemplos de la derivada de la cosecante

Vista cuál es la fórmula de la derivada de la cosecante, pasamos ahora a hacer varios ejemplos. Así podrás ver exactamente cómo se deriva la cosecante de una función.

Ejemplo 1: Derivada de la cosecante de 2x

En este ejemplo veremos cuánto vale la derivada de la cosecante de 2x:

$f(x)=\text{cosec}(2x)$

La función del argumento de la cosecante es diferente de x, por lo tanto, debemos usar la regla de la derivada de la cosecante con la regla de la cadena.

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

Entonces, para hallar la derivada de esta función trigonométrica simplemente tenemos que sustituir los valores en la fórmula anterior: en el argumento del coseno y del seno ponemos 2x, y u’ corresponde a la derivada de 2x, que es 2:

$f(x)=\text{cosec}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2\cdot \text{cos}(2x)}{\text{sen}^2(2x)}$

Ejemplo 2: Derivada de la cosecante de x al cuadrado

En este ejercicio veremos cuánto es la derivada de la cosecante de x al cuadrado:

$f(x)=\text{cosec}(x^2)$

Lógicamente, la derivada de esta función trigonométrica se resuelve utilizando la fórmula de la derivada de la cosecante:

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

La derivada de x al cuadrado da 2x, así que la derivada de la cosecante de x elevada a la dos es:

$f(x)=\text{cosec}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x\cdot \text{cos}(x^2)}{\text{sen}^2(x^2)}$

Ejemplo 3: Derivada de la cosecante al cubo de una función exponencial

$f(x)=\text{cosec}^3(e^{5x})$

Independientemente de la función del argumento, la regla de la derivada de la cosecante de una función es:

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

Pero en este caso tenemos una función compuesta, porque la cosecante está elevada a la tres y, además, en su argumento hay una función exponencial. De modo que para hacer la derivación de toda la función tenemos que aplicar la regla de la cadena varias veces:

$\begin{aligned}\displaystyle f'(x)& = 3\text{cosec}^2(e^{5x})\cdot\left(-\frac{5e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\right)\\[1.5ex]&=-\frac{-15\text{cosec}^2(e^{5x})\cdot e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\end{aligned}$

Ejercicios resueltos de la derivada de la cosecante

Deriva las siguientes funciones cosecante:

$\text{A) }f(x)=\text{cosec}(x^4-2x^2)$

$\text{B) }f(x)=\text{cosec}(x^3+e^x-10)$

$\text{C) }f(x)=\text{cosec}\bigl(\ln(x^3+7x^2)\bigr)$

$\text{D) }f(x)=\text{cosec}\bigl(\text{arccos}(x^7)\bigr)$

$\text{E) }f(x)=\text{cosec}\left(\sqrt{9x^2-4x}\right)$

Ver solución

$\text{A) }f('x)=-\cfrac{(4x^3-4x)\cdot \text{cos}(x^4-2x^2)}{\text{sen}^2(x^4-2x^2)}$

$\text{B) }f('x)=-\cfrac{(3x^2+e^x)\cdot \text{cos}(x^3+e^x-10)}{\text{sen}^2(x^3+e^x-10)}$

$\begin{aligned}\text{C) }f'(x)& =-\cfrac{\cfrac{3x^2+14x}{x^3+7x^2}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{\cfrac{3x+14}{x^2+7x}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{(3x+14)\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{(x^2+7x)\cdot \text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\end{aligned}$

$\begin{aligned}\text{D) }f'(x)& =-\cfrac{-\cfrac{7x^6}{\sqrt{1-\left(x^7\right)^2}}\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =-\cfrac{(-7x^6)\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =\cfrac{7x^6\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\end{aligned}$

$\begin{aligned} \text{E) }f'(x)& =-\cfrac{\cfrac{18x-4}{2\cdot\sqrt{9x^2-4x}} \cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{\text{sen}^2\left(\sqrt{9x^2-4x}\right)}\\[1.5ex] &=-\cfrac{(18x-4)\cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{2\sqrt{9x^2-4x}\cdot \text{sen}^2\left(\sqrt{9x^2-4x}\right)} \end{aligned}$

Demostración de la fórmula de la derivada de la cosecante

A continuación, vamos a demostrar la fórmula de la derivada de la cosecante. A diferencia de otras demostraciones, en este caso no utilizaremos el límite que define una derivada, sino que partiremos de la definición matemática de la cosecante.

Algebraicamente, la función trigonométrica cosecante es el inverso multiplicativo del seno:

$f(x)=\text{cosec}(x)=\cfrac{1}{\text{sen}(x)}$

De manera que podemos hacer la derivada de la cosecante usando la regla del cociente:

$f'(x)=\cfrac{0\cdot \text{sen}(x)-1\cdot \text{cos}(x)}{\text{sen}^2(x)}$

$f'(x)=\cfrac{-\text{cos}(x)}{\text{sen}^2(x)}$

Como puedes comprobar, solo aplicando la regla de la derivada de una división llegamos a la fórmula de la derivada de la cosecante. Y como la derivada de un cociente ya está demostrada (puedes verla en el siguiente enlace), la regla de la derivada de la cosecante también queda demostrada.

➤ Ver: demostración de la derivada de un cociente

Fórmula de la derivada de la cosecante

Ejemplos de la derivada de la cosecante

Ejemplo 1: Derivada de la cosecante de 2x

Ejemplo 2: Derivada de la cosecante de x al cuadrado

Ejemplo 3: Derivada de la cosecante al cubo de una función exponencial

Ejercicios resueltos de la derivada de la cosecante

Demostración de la fórmula de la derivada de la cosecante

Deja un comentario Cancelar respuesta