Derivada de un cociente (división): fórmula y ejercicios resueltos

En este post te explicamos cómo derivar un cociente (o división) de dos funciones. Encontrarás ejemplos de derivadas de cocientes de funciones y, además, podrás practicar con ejercicios resueltos paso a paso de derivadas de divisiones.

Índice

Fórmula de la derivada de un cociente

La derivada de un cociente (o una división) de dos funciones es igual al cociente de la derivada de la función del numerador por la función del denominador menos la función del numerador por la derivada de la función del denominador dividido por la función del denominador elevada al cuadrado.

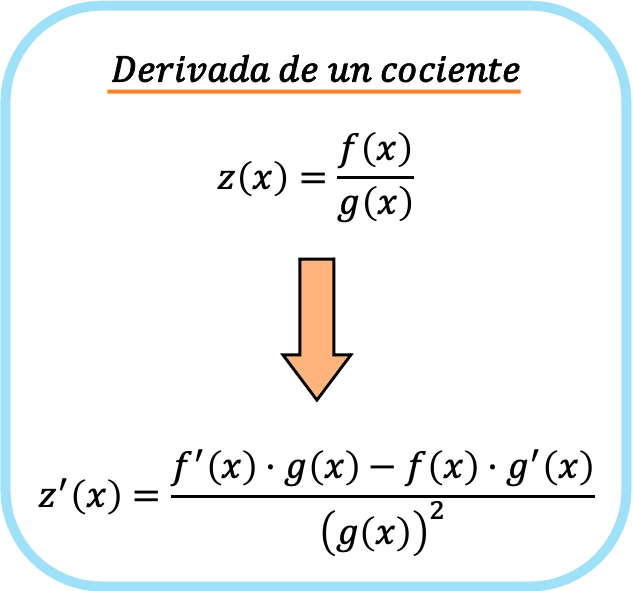
formula de la derivada de una division o de un cociente

Como puedes ver, al aplicar la regla de la derivada de un cociente (o una división) seguimos teniendo una fracción después de la derivación. Pero, además, en el numerador tenemos dos multiplicaciones y una resta, y el denominador está elevado a la dos.

Ejemplos de derivadas de cocientes

Acabamos de ver cuál es la fórmula de la derivada de un cociente de dos funciones, a continuación, resolveremos varios ejemplos de derivadas de este tipo de operaciones. Recuerda que si no entiendes cómo se deriva un cociente de funciones puedes preguntarnos en la sección de comentarios.

Ejemplo 1

En este ejemplo derivaremos una función potencial dividida entre una función trigonométrica:

$f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}$

La fórmula de la derivada de una división de dos funciones diferentes es la siguiente:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

De manera que primero debemos calcular la derivada de cada función por separado:

$\cfrac{d}{dx}\ (3x^2+4x)=6x+4$

$\cfrac{d}{dx}\ \text{sen}(2x)=2\text{cos}(2x)$

Por lo tanto, la derivada de toda la función es:

$\begin{array}{c}f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(6x+4)\cdot\text{sen}(2x)-(3x^2+4x)\cdot 2\text{cos}(2x)}{\text{sen}^2(2x)}\end{array}$

Ejemplo 2

En este caso hallaremos la derivada de una constante dividida entre una función:

$f(x)=\cfrac{10}{x^2+3x-9}$

Como hemos visto más arriba, la regla de la derivada de una división de dos funciones distintas es la siguiente:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Entonces, calculamos la derivada del numerador y del denominador por separado:

$\cfrac{d}{dx}\ 10=0$

$\cfrac{d}{dx}\ (x^2+3x-9)=2x+3$

Y, finalmente, hallamos la derivada de toda la división:

$\begin{array}{c}f(x)=\cfrac{10}{x^2+3x-9}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{0\cdot (x^2+3x-9)-10\cdot (2x+3)}{\left(x^2+3x-9\right)^2}=\cfrac{-20x+30}{\left(x^2+3x-9\right)^2}\end{array}$

De hecho, podemos deducir una fórmula para derivar directamente cuando tenemos una constante en el numerador dividida por una función, porque la derivada de la constante siempre es 0. Por tanto, siempre se cumplirá la siguiente fórmula:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=\cfrac{k}{f(x)} \\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{-k\cdot f'(x)}{\bigl(f(x)\bigr)^2}\end{array} \end{empheq}$

Ejemplo 3

En este ejercicio derivaremos un cociente de dos polinomios:

$f(x)=\cfrac{x^3+4x^2}{5x^2-8}$

Para resolver la derivada, debemos aplicar la regla de la derivada de un cociente de dos funciones distintas, que es la siguiente:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Ahora hallamos la derivada del polinomio del numerador y del polinomio del denominador:

$\cfrac{d}{dx}\ (x^3+4x^2)=3x^2+8x$

$\cfrac{d}{dx}\ (5x^2-8)=10x$

Así que la derivada de la división de polinoimos es:

$\begin{array}{c}f(x)=\cfrac{x^3+4x^2}{5x^2-8}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\end{array}$

Y, por último, hacemos las operaciones y simplificamos al máximo la fracción:

$\begin{aligned}f'(x)&=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\\[2ex]&=\cfrac{15x^4-24x^2+40x^3-64x-10x^4-40x^3}{25x^4+64-80x^2}\\[2ex]&=\cfrac{5x^4-24x^2-64x}{25x^4-80x^2+64}\end{aligned}$

Ejercicios resueltos de la derivada de un cociente

Deriva las siguientes divisiones de funciones:

$\text{A) }f(x)=\cfrac{9x^2+5x}{6x^3}$

$\text{B) }f(x)=\cfrac{19}{2x^2-2}$

$\text{C) }f(x)=\cfrac{8x^3-4x^2+3x}{e^{4x}}$

$\text{D) }f(x)=\cfrac{\text{cos}(x^2)}{\text{sen}(6x)}$

$\text{E) }f(x)=\cfrac{\ln(x^3+4)}{\left(4x^2-3x\right)^3}$

$\text{F) }f(x)=\cfrac{\sqrt{x^2+4x}}{5^{x^2}}$

Ver solución

$\begin{aligned}\text{A) }f'(x)&=\cfrac{(18x+5)\cdot 6x^3-(9x^2+5x)\cdot 18x^2}{\left(6x^3\right)^2}\\[1.5ex]&=\cfrac{108x^4+30x^3-162x^4-90x^3}{36x^6}\\[1.5ex]&=\cfrac{-54x^4-60x^3}{36x^6}\\[1.5ex]&=\cfrac{-9x-10}{6x^3}\end{aligned}$

$\text{B) }f'(x)=\cfrac{-19\cdot 4x}{\left(2x^2-2\right)^2}=\cfrac{-76x}{\left(2x^2-2\right)^2}$

$\begin{aligned}\text{C) }f'(x)&=\cfrac{(24x^2-8x+3)e^{4x}-(8x^3-4x^2+3x)\cdot 4e^{4x}}{\left(e^{4x}\right)^2}\\[1.5ex]&=\cfrac{e^{4x}(24x^2-8x+3-32x^3+16x^2-12x)}{e^{8x}}\\[1.5ex]&=\cfrac{-32x^3+40x^2-20x+3}{e^{4x}}\end{aligned}$

$\text{D) }f'(x)=\cfrac{-2x\text{sen}(x^2)\cdot\text{sen}(6x)-\text{cos}(x^2)\text{cos}(6x)\cdot 6}{\text{sen}^2(6x)}$

$\begin{aligned}\text{E) }f'(x)&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(\left(4x^2-3x\right)^3\right)^2}\\[1.5ex]&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(4x^2-3x\right)^6}\end{aligned}$

$\begin{aligned}\text{F) }f'(x)&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{\left(5^{x^2}\right)^2}\\[1.5ex]&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{5^{2x^2}}\end{aligned}$

Demostración de la derivada de un cociente

Por último, vamos a demostrar la fórmula de la derivada de una división. Para ello, utilizaremos la definición general de una derivada, que es:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Sea z un división de dos funciones diferentes:

$z(x)=\cfrac{f(x)}{g(x)}$

Entonces, la derivada de la función z aplicando la definición matemática será:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\cfrac{f(x+h)}{g(x+h)}-\cfrac{f(x)}{g(x)}}{h}$

Resolvemos la resta de fracciones del numerador de la fracción:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\cfrac{f(x+h)\cdot g(x)}{g(x+h)\cdot g(x)}-\cfrac{f(x)\cdot g(x+h)}{g(x)\cdot g(x+h)}}{h}$

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x)-f(x)\cdot g(x+h)}{h\cdot g(x)\cdot g(x+h)}$

Al añadir un término sumando y restando en una ecuación, esta no se modifica. De modo que podemos hacer el siguiente paso:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x)\color{orange}\bm{-f(x)\cdot g(x)}\color{black}-f(x)\cdot g(x+h)\color{orange}\bm{+f(x)\cdot g(x)}\color{black}}{h\cdot g(x)\cdot g(x+h)}$

Extraemos factor común:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{g(x)\bigl[f(x+h)-f(x)\bigr]-f(x)\bigl[g(x+h)-g(x)\bigr]}{h\cdot g(x)\cdot g(x+h)}$

Ahora pasamos el término h del denominador al numerador usando las propiedades de las fracciones:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{g(x)\cdot \cfrac{f(x+h)-f(x)\cdot g(x)}{h}-f(x)\cdot\cfrac{g(x+h)-g(x)}{h}}{g(x)\cdot g(x+h)}$

Transformamos la ecuación aplicando las propiedades de los límites:

$\displaystyle f'(x)=\frac{g(x)\cdot \displaystyle\lim_{h \to 0}\cfrac{f(x+h)-f(x)\cdot g(x)}{h}-f(x)\cdot\lim_{h \to 0}\cfrac{g(x+h)-g(x)}{h}}{g(x)\cdot \displaystyle\lim_{h \to 0}g(x+h)}$

Los límites del numerador corresponden justamente a la definición matemática de la derivada de cada función, por tanto:

$\displaystyle f'(x)=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)\cdot \displaystyle\lim_{h \to 0}g(x+h)}$

Resolvemos el límite del denominador de la fracción:

$\displaystyle f'(x)=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)\cdot g(x)}$

Y de esta forma queda demostrada la fórmula de la derivada de un cociente de dos funciones:

$\displaystyle f'(x)=\frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}$

4 comentarios en “Derivada de un cociente (o división)”

Sonia
04/03/2022 a las 16:33

Buenos días me gustaría saber si tiene resolución de ejercicios de derivadas de cocientes pero con exponentes fraccionarios y de productos pero con doble producto en el numerador
Saludos

Responder
1. Funciones
  09/03/2022 a las 15:07
  
  Hola Sonia,
  
  Todos los ejercicios resueltos de derivadas de divisiones están incluidos en este post. De la misma manera, todas los ejercicios resueltos de derivadas de multiplicadas están publicados en el post de la derivada de un producto.
  
  ¡Pero lo apunto para incluirlo en el futuro!
Juan David
06/07/2022 a las 02:08

Buen día, creo que hay un error en el ejercicio D de los últimos ejercicios resueltos, la respuesta en el numerador el resultado me dio:
– 2x sin(x^2) sin(6x) – 6 cos(x^2) cos(6x)

Por favor podrías revisar el punto?
Por cierto, aprovecho para agradecerte este y los demás artíulos de esta grandiosa página. Un saludo 🙂

Responder
1. Funciones
  11/07/2022 a las 13:16
  
  Hola Juan David,
  
  Tienes razón, en el numerador había un coseno que debería ser un seno, ya se ha corregido. 👍
  
  ¡Gracias por avisar y por tu apoyo a esta página web!

Fórmula de la derivada de un cociente

Ejemplos de derivadas de cocientes

Ejemplo 1

Ejemplo 2

Ejemplo 3

Ejercicios resueltos de la derivada de un cociente

Demostración de la derivada de un cociente

4 comentarios en “Derivada de un cociente (o división)”

Deja un comentario Cancelar respuesta