En esta página verás cuál es la fórmula de la derivada del arcocosecante. Además, podrás ver ejercicios resueltos de derivadas del arcocosecante de una función.
Índice
Fórmula de la derivada del arcocosecante
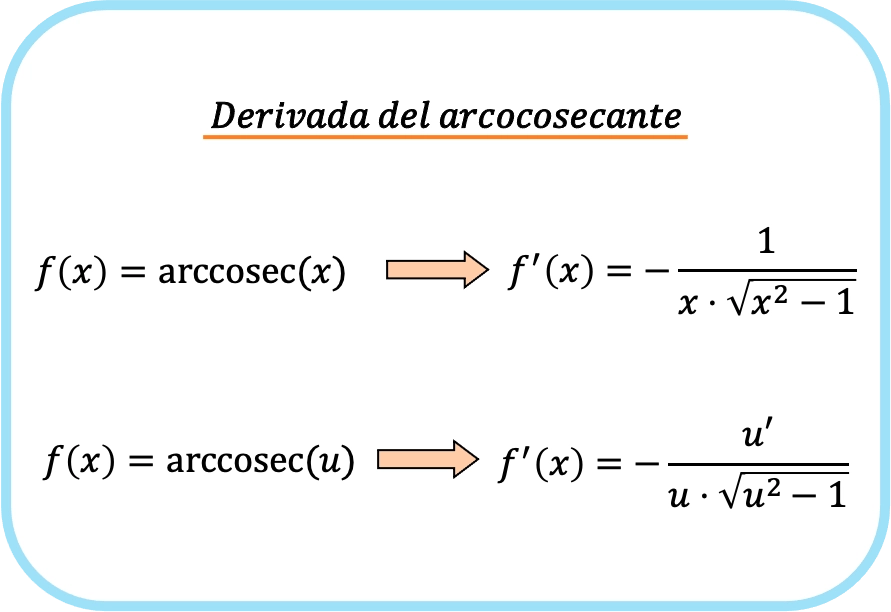
La derivada del arcocosecante de x es menos uno partido por el producto de x por la raíz de x al cuadrado menos 1.
Por lo tanto, la derivada del arcocosecante de una función es igual a menos el cociente de la derivada de esa función dividido por la función por la raíz de dicha función al cuadrado menos uno.
En realidad, las dos fórmulas anteriores son la misma, pero en la segunda expresión está aplicada la regla de la cadena. De hecho, si sustituyes en la u la función identidad x, obtendrás la derivada del arcocosecante de x ya que la derivada de x es uno.
Como bien sabes, el arcocosecante es la función trigonométrica inversa de la cosecante, sin embargo, sus derivadas son bastante distintas. Puedes ver la fórmula de este otro tipo de función trigonométrica en el siguiente enlace:
➤ Ver: derivada de la cosecante
Ejemplos de la derivada del arcocosecante
Vista cuál es la regla de la derivada del arcocosecante, a continuación resolveremos dos ejemplos de este tipo de derivada. Pero si igualmente te queda alguna duda de cómo derivar el arcocosecante, puedes preguntarnos en los comentarios.
Ejemplo 1
En este ejemplo veremos cuánto es la derivada del arcocosecante de la función cuadrática x2.
Para calcular la derivada del arcocosecante de x al cuadrado, aplicamos la fórmula que hemos visto más arriba:
La derivada de x elevada a la dos es 2x, de modo que la derivada de la función compuesta es:
Ejemplo 2
En este segundo ejemplo derivaremos el arcocosecante de una función potencial.
Tenemos que usar la regla de la derivada del arcosecante para hallar la derivada de toda la función.
Entonces, en el numerador escribimos la derivada del argumento de la función, y en el denominador reescribimos la función potencial y la multiplicamos por la raíz cuadrada de la función del argumento elevada al cuadrado menos 1:

