Aquí encontrarás cómo derivar la función coseno (fórmula). Podrás ver ejemplos de derivadas de funciones coseno y practicar con ejercicios resueltos paso a paso. Además, te mostramos la demostración de la fórmula, cuál es la segunda derivada del coseno e, incluso, la derivada del coseno inverso.
Índice
¿Cuál es la derivada del coseno?
La derivada de la función coseno es la función seno cambiada de signo. Es decir, la derivada del coseno de x es igual a menos el seno de x.
Si en el argumento del coseno hay una función, la derivada del coseno es el producto de menos el seno de esa función por la derivada de la función.
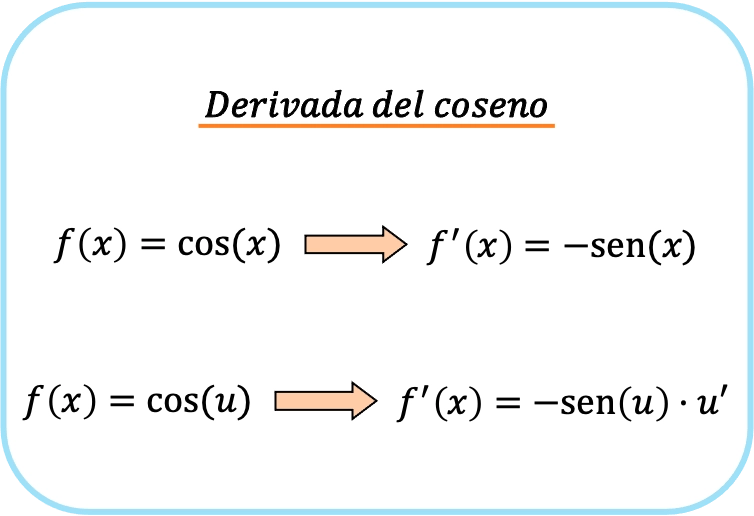
La segunda fórmula es equivalente a la primera fórmula pero aplicando la regla de la cadena. Así pues, a modo de resumen, la fórmula de la derivada del coseno es la siguiente:
Ejemplos de la derivada del coseno
Ahora que ya sabemos cuál es la fórmula del coseno, vamos a explicar varios ejemplos de este tipo de derivadas trigonométricas para que no te quede ninguna duda acerca de cómo derivar la función coseno.
Ejemplo 1: Derivada del coseno de 2x
En el argumento del coseno no tenemos una sola x, sino que tenemos una función más compleja. Por lo tanto, debemos emplear la siguiente fórmula para derivar el coseno:
Como la derivada de 2x es 2, la derivada del coseno de 2x será menos el seno de 2x multiplicado por 2.
Ejemplo 2: Derivada del coseno de x al cuadrado
Al igual que en el ejemplo anterior, en el argumento del coseno tenemos una función diferente de x, por lo que utilizaremos la regla de la cadena para derivar el coseno:
Entonces, la derivada de x2 es 2x, en consecuencia, la derivada del coseno de x elevada a la 2 es:
Ejemplo 3: Derivada del coseno al cubo
La función coseno de este ejemplo está compuesta por otra función, así que tenemos que aplicar la siguiente fórmula para resolver la derivada:
Así pues, aplicando la fórmula, llegamos a la derivada de la función:
![\begin{aligned}f'(x)&=3\text{cos}^2(2x^6-5x^3)\cdot \bigl(-\text{sen}(2x^6-5x^3)\bigr)\cdot (12x^5-15x^2)\\[2ex]&=-3\text{cos}^2(2x^6-5x^3)\cdot \text{sen}(2x^6-5x^3)\cdot (12x^5-15x^2)\end{aligned}](https://www.funciones.xyz/wp-content/ql-cache/quicklatex.com-2af8e30626bb049a4bf33b517a77aa8d_l3.svg "Rendered by QuickLaTeX.com")
➤ Para poder derivar esta función también debes utilizar la fórmula de la derivada de una función potencial.
Segunda derivada del coseno
Seguidamente, vamos a ver que la la segunda derivada del seno se puede calcular fácilmente, debido a las características de las funciones trigonométricas.
➤ Nota: para entender lo siguiente debes saber cuál es la derivada del seno.
La segunda derivada del coseno de x es menos el coseno de x. Puede parecer raro, pero matemáticamente es así. Esto es debido a que la derivada del seno es el coseno y, por tanto, al derivar dos veces el coseno de x se vuelve a obtener el coseno pero cambiado de signo.
![\begin{array}{c}f(x)=\text{cos}(x)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(x)\\[2ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(x)\end{array}](https://www.funciones.xyz/wp-content/ql-cache/quicklatex.com-045767c89e7a8a775cdcfe1ad2cc5c75_l3.svg "Rendered by QuickLaTeX.com")
Esta propiedad cambia si el argumento del coseno no es x, ya que en tal caso arrastramos el término de la regla de la cadena:
![\begin{array}{c}f(x)=\text{cos}(u)\\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f'(x)=-\text{sen}(u)\cdot u' \\[1.5ex] \quad\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex] f''(x)=-\text{cos}(u)\cdot u'^2 -\text{sen}(u)\cdot u'' \end{array}](https://www.funciones.xyz/wp-content/ql-cache/quicklatex.com-b0c566c3e4a7f382621a9055d5e34798_l3.svg "Rendered by QuickLaTeX.com")
Derivada del coseno inverso
Todas las funciones trigonométricas tienen función inversa y, como tal, la función coseno también se puede invertir. Asimismo, el coseno inverso es derivable.
La derivada del coseno inverso de una función es menos la derivada de la función partido por la raíz cuadrada de uno menos el cuadrado de dicha función.
Recuerda que el coseno inverso también se llama arcocoseno.
Por ejemplo, la derivada del coseno inverso de 3x es:
Ejercicios resueltos de la derivada del coseno
Calcula la derivada de las siguientes funciones coseno:
![\begin{aligned}\text{F) }\displaystyle f'(x)&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x\cdot 5x-e^x\cdot 5}{(5x)^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{5e^x(x-1)}{25x^2}\\[2ex]&=-9\text{sen}\left(\frac{e^x}{5x}\right)\cdot \frac{e^x(x-1)}{5x^2}\end{aligned}](https://www.funciones.xyz/wp-content/ql-cache/quicklatex.com-df84bdec7a08bb63d320dfe07260c1bd_l3.svg "Rendered by QuickLaTeX.com")
Demostración de la derivada del coseno
Finalmente, vamos a demostrar matemáticamente la fórmula de la derivada del coseno de x. Para ello, utilizaremos la definición de la derivada, que corresponde al siguiente límite:
Vamos a hacer la demostración del coseno, así que la función es cos(x):
Este límite no lo podemos resolver por sustitución, ya que llegaríamos a una indeterminación. Sin embargo, podemos expresar de otra manera el coseno de una suma aplicando la siguiente identidad trigonométrica:
El siguiente paso consiste en separar la fracción en dos fracciones y sacar factor común del coseno:
![\displaystyle f'(x)=\lim_{h \to 0}\left[\frac{\text{cos}(x)\bigl(\text{cos}(h)-1\bigr)}{h}-\frac{\text{sen}(x)\text{sen}(h)}{h}\right]](https://www.funciones.xyz/wp-content/ql-cache/quicklatex.com-476721252a721359685934e5513e4936_l3.svg "Rendered by QuickLaTeX.com")
El límite de una resta es igual a la resta de los límites, por tanto:
Tanto el coseno de x como el seno de x no dependen de h, de modo que los podemos extraer fuera de los límites:
Utilizando el cálculo de límites por infinitésimos equivalentes, llegamos a la conclusión de que el primer límite vale 0 y el segundo límite vale 1. Por tanto:
Y ya hemos llegado a la fórmula de la derivada de la función coseno, por lo que queda demostrada la igualdad.
