Derivada del arcocoseno hiperbólico

En esta página verás cuál es la derivada del arcocoseno hiperbólico (fórmula). También encontrarás ejercicios resueltos paso a paso de derivadas del arcocoseno hiperbólico de una función. Y, por último, hallarás la demostración de la fórmula de la derivada de este tipo de función trigonométrica.

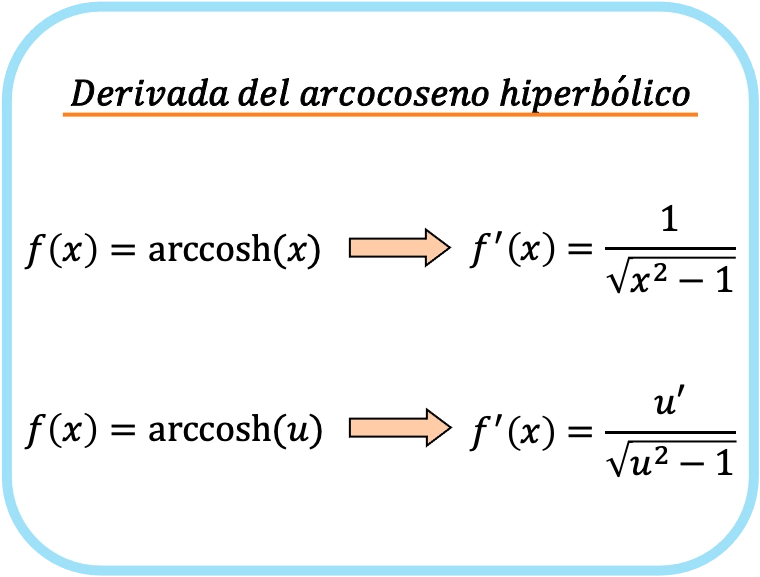
Fórmula de la derivada del arcocoseno hiperbólico

La derivada del arcocoseno hiperbólico de x es uno partido por la raíz cuadrada de x al cuadrado menos 1.

f(x)=\text{arccosh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{x^2-1}}

Por lo tanto, la derivada del arcocoseno hiperbólico de una función es igual al cociente de la derivada de esa función partido por la raíz cuadrada dicha función al cuadrado menos uno.

f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}

La segunda fórmula incluye la regla de la cadena y, por tanto, se puede utilizar para derivar cualquier arcocoseno hiperbólico. De hecho, si sustituimos la u por x obtendremos la primera fórmula. En cambio, la primera fórmula solo sirve para la derivada del arcocoseno hiperbólico de x.

derivada del arcocoseno hiperbolico

El arcocoseno hiperbólico es la función inversa del coseno hiperbólico y, por lo tanto, ambas funciones están relacionadas. Puedes ver la fórmula de la derivada de esta función trigonométrica haciendo click aquí:

➤ Ver: fórmula de la derivada del coseno hiperbólico

Ejemplos de la derivada del arcoseno hiperbólico

Ejemplo 1

f(x)=\text{arccosh}(5x)

Para hallar la derivada del arcocoseno hiperbólico tenemos que emplear su fórmula correspondiente, que es:

f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}

Por tanto, en el numerador de la fracción tenemos que poner la derivada de 5x, que es 5. Y en el denominador simplemente debemos poner la raíz cuadrada de la función del argumento elevada al cuadrado menos 1:

f(x)=\text{arccosh}(5x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{5}{\sqrt{(5x)^2-1}}=\cfrac{5}{\sqrt{25x^2-1}}

Ejemplo 2

f(x)=\text{arccosh}(x^4-5x^2)

La función a derivar de este ejercicio es un arcocoseno hiperbólico, por lo que usamos la siguiente fórmula para hacer su derivación:

f(x)=\text{arccosh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2-1}}

Entonces, en el numerador escribimos la derivada del argumento de la función y en el denominador la raíz cuadrada de la función del argumento elevada a la 2 menos 1:

f(x)=\text{arccosh}(x^4-5x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{4x^3-10x}{\sqrt{\left(x^4-5x^2\right)^2-1}}

Demostración de la derivada del arcocoseno hiperbólico

Para terminar, demostraremos la fórmula de la derivada del arcocoseno hiperbólico.

y=\text{arccosh}(x)

En primer lugar, transformamos el arcocoseno hiperbólico en coseno hiperbólico :

x=\text{cosh}(y)

Derivamos en los dos lados de la igualdad:

1=\text{senh}(y)\cdot y'

Despejamos y’:

y'=\cfrac{1}{\text{senh}(y)}

Ahora utilizamos la identidad trigonométrica que relaciona el seno hiperbólico y el coseno hiperbólico para hacer un cambio en el denominador:

\text{cosh}^2(y)-\text{senh}^2(y)=1 \ \longrightarrow \ \text{senh}(y)=\sqrt{\text{cosh}^2(y)-1}

y'=\cfrac{1}{\sqrt{\text{cosh}^2(y)-1}}

Sin embargo, al principio hemos deducido que x es equivalente al coseno hiperbólico de y, por lo que la ecuación queda:

y'=\cfrac{1}{\sqrt{x^2-1}}

Artículos relacionados

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *