Derivada de la arcotangente hiperbólica (fórmula y ejemplos)

Aquí encontrarás cómo derivar la arcotangente hiperbólica de una función. También podrás ver ejemplos resueltos de este tipo de derivadas trigonométricas y, por último, te demostramos la fórmula de la derivada de la arcotangente hiperbólica.

Índice

Fórmula de la derivada de la arcotangente hiperbólica

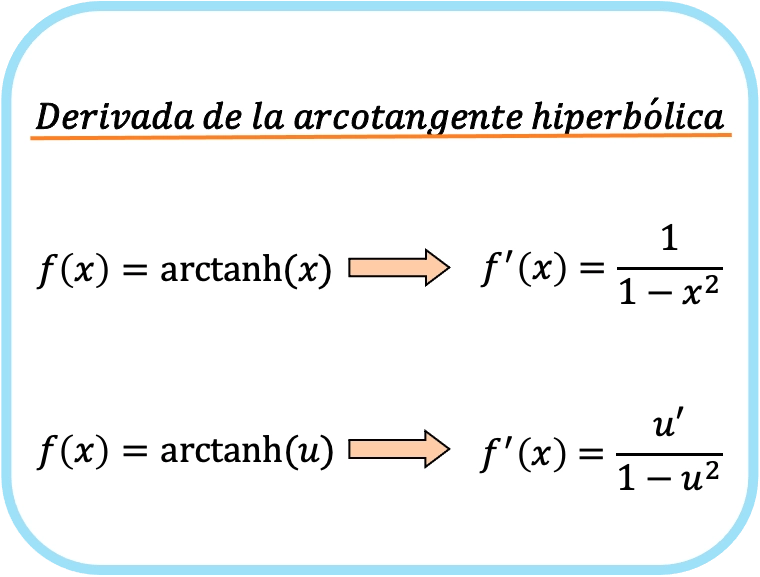
La derivada de la arcotangente hiperbólica de x es uno partido por uno menos x al cuadrado.

$f(x)=\text{arctanh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{1-x^2}$

Por lo tanto, la derivada de la arcotangente hiperbólica de una función es igual al cociente de la derivada de esa función partido por uno menos dicha función al cuadrado.

$f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}$

En realidad las dos fórmulas son la misma, pero en la segunda está aplicada la regla de la cadena. Por ejemplo, al sustituir la u por una x, nos da exactamente la primera fórmula ya que la derivada de x es 1.

Del mismo modo que el arcotangente es la función inversa de la tangente, el arcotangente hiperbólico es la inversa de la tangente hiperbólica. Aún así, sus derivadas son muy diferentes, puedes consultar la derivada de esta función trigonométrica aquí:

➤ Ver: fórmula de la derivada de la tangente hiperbólica

Ejemplos de la derivada de la arcotangente hiperbólica

Ejemplo 1

$f(x)=\text{arctanh}(2x)$

Lógicamente, tenemos que aplicar la regla de la derivada de la arcotangente hiperbólica:

$f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}$

La derivada de 2x es 2, por lo tanto, en el numerador de la fracción debemos poner un dos y en el denominador uno menos 2x al cuadrado:

$f(x)=\text{arctanh}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{1-(2x)^2}}=\cfrac{2}{1- 4x^2}$

Ejemplo 2

$f(x)=\text{arctanh}(e^{3x})$

Para resolver la derivada de esta función debemos utilizar la fórmula de la derivada de la arcotangente hiperbólica.

$f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}$

Además, la función del argumento de la arcotangente hiperbólica es una función compuesta, por lo que también tendremos que aplicar la regla de la cadena:

$f(x)=\text{arctanh}(e^{3x}) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3\cdot e^{3x}}{1-\left(e^{3x}\right)^2}=\cfrac{3e^{3x}}{1-3^{6x}}$

Demostración de la derivada de la arcotangente hiperbólica

En este último apartado, vamos a demostrar la fórmula de la derivada de la arcotangente hiperbólica.

$y=\text{arctanh}(x)$

Dado que la arcotangente hiperbólica es la tangente hiperbólica invertida, podemos expresar la igualdad anterior de otra forma:

$x=\text{tanh}(y)$

Ahora derivamos en los dos lados de la ecuación:

$1=\cfrac{1}{\text{cosh}^2(y)}\cdot y'$

Despejamos y’:

$y'=\text{cosh}^2(y)$

Por otra parte, sabemos que la diferencia de los cuadrados del coseno hiperbólico y del seno hiperbólico da 1. De modo que podemos transformar la expresión anterior en una fracción:

$\text{cosh}^2(y)-\text{senh}^2(y)=1$

$y'=\cfrac{\text{cosh}^2(y)}{1}=\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)-\text{senh}^2(y)}$

Dividimos todos los términos de la fracción entre el cuadrado del coseno hiperbólico:

$y'=\cfrac{\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)}}{\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)}-\cfrac{\text{senh}^2(y)}{\text{cosh}^2(y)}}$

$y'=\cfrac{1}{1-\cfrac{\text{senh}^2(y)}{\text{cosh}^2(y)}}$

El cociente del seno hiperbólico entre el coseno hiperbólico es igual a la tangente hiperbólica, por tanto:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

$y'=\cfrac{1}{1-\text{tanh}^2(y)}$

Pero, como hemos visto al principio de la demostración, la tangente hiperbólica es equivalente a la variable x, así que podemos sustituir la expresión consiguiendo así la fórmula de la derivada de la arcotangente hiperbólica:

$y'=\cfrac{1}{1-x^2}$

Derivada de la arcotangente hiperbólica

Fórmula de la derivada de la arcotangente hiperbólica

Ejemplos de la derivada de la arcotangente hiperbólica

Ejemplo 1

Ejemplo 2

Demostración de la derivada de la arcotangente hiperbólica

Artículos relacionados

Deja un comentario Cancelar respuesta