▷ Derivada de la cotangente hiperbólica (fórmula y ejemplos)

Aquí te explicamos cómo derivar la cotangente hiperbólica de una función. También encontrarás ejemplos de la derivada de la cotangente hiperbólica.

Índice

Fórmula de la derivada de la cotangente hiperbólica

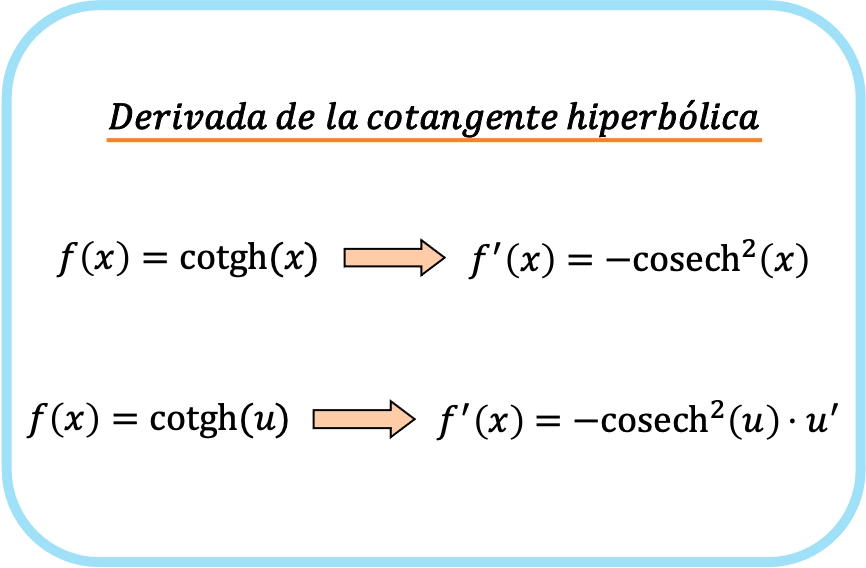
La derivada de la cotangente hiperbólica de x es igual a menos la cosecante hiperbólica de x al cuadrado.

$f(x)=\text{cotgh}(x)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(x)$

Por lo tanto, la derivada de la cotangente hiperbólica de una función es menos la cosecante hiperbólica de la función al cuadrado por la derivada de dicha función.

$f(x)=\text{cotgh}(u)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(u)\cdot u'$

Ten presente que en la segunda fórmula se ha aplicado la regla de la cadena, y esta fórmula se utiliza cuando en el argumento de la cotangente hiperbólica hay una función diferente de x.

Puede que en algunos libros de matemáticas encuentres que la derivada de la cotangente sea otra, ya que las siguientes tres expresiones son equivalentes:

$f'(x)=-\text{cosech}^2(x)=1-\text{cotgh}^2(x)=-\cfrac{1}{\text{senh}^2(x)}$

Obviamente puedes utilizar la expresión que prefieras de las tres para derivar la cotangente hiperbólica, pero la más utilizada es la cosecante hiperbólica al cuadrado.

Ejemplos de la derivada de la cotangente hiperbólica

Una vez sabemos cuál es la fórmula de la derivada de la cotangente hiperbólica de una función, vamos a resolver varios ejemplos de este tipo de derivadas trigonométricas.

Ejemplo 1

En este ejemplo veremos cuál es la derivada de la cotangente hiperbólica de la función 2x.

$f(x)=\text{cotgh}(2x)$

En el argumento de la cotangente hiperbólica tenemos una función distinta de x, por lo que debemos usar la fórmula con la regla de la cadena para hacer la derivación:

$f(x)=\text{cotgh}(u)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(u)\cdot u'$

Como 2x és un término de primer grado, su derivada es 2. De modo que para hallar la derivada de la cotangente hiperbólica de 2x simplemente debemos poner 2x en el argumento de la cosecante hiperbólica al cuadrado y multiplicarla por 2.

$f(x)=\text{cotgh}(2x)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(2x)\cdot 2$

Ejemplo 2

En el segundo ejemplo determinaremos cuánto vale la derivada de la cotangente hiperbólica de una función polinómica.

$f(x)=\text{cotgh}(3x^4-5x)$

Como hemos visto más arriba, la regla para derivar la cotangente hiperbólica de una función es la siguiente:

$f(x)=\text{cotgh}(u)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(u)\cdot u'$

Por lo tanto, la derivada de la cotangente hiperbólica de este ejercicio será la siguiente:

$f(x)=\text{cotgh}(3x^4-5x)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(3x^4-5x)\cdot(12x^3-5)$

Fórmula de la derivada de la cotangente hiperbólica

Ejemplos de la derivada de la cotangente hiperbólica

Ejemplo 1

Ejemplo 2

Deja un comentario Cancelar respuesta