Aquí encontrarás cuál es la fórmula de la derivada del arcocotangente y te explicaremos cómo derivar el arcocotangente de una función con ejemplos.
Índice
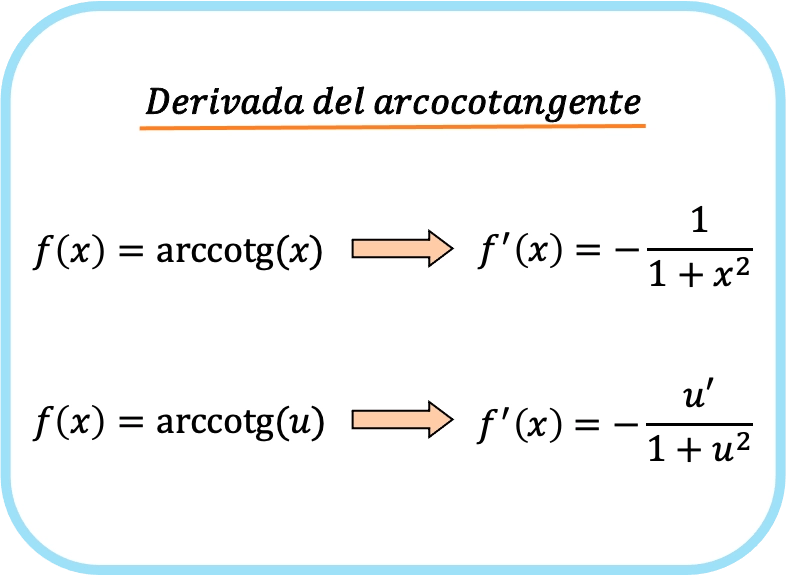
Fórmula de la derivada del arcocotangente
La derivada del arcotangente de x es menos uno partido por uno más x al cuadrado.
Por lo tanto, la derivada del arcocotangente de una función es igual a menos la derivada de esa función dividida por uno más la función elevada al cuadrado.
Ten en cuenta que la primera y la segunda fórmula son la misma, la única diferencia es que en la segunda expresión está aplicada la regla de la cadena. De hecho, si sustituyes la u por una x, obtendrás la primera fórmula ya que la derivada de la función x es 1.
A pesar de que el arcocotangente es la función inversa de la cotangente, sus derivadas son bastante distintas. De hecho, la cotangente de una función tiene tres maneras de derivarse, puedes ver todas ellas aquí:
➤ Ver: fórmula de la derivada de la cotangente
Ejemplos de la derivada del arcocotangente
Después de ver cuál es la fórmula de la derivada del arcocotangente, a continuación tienes dos ejercicios resueltos de este tipo de derivada trigonométrica. Recuerda también que si tienes alguna duda puedes dejar tu pregunta abajo en los comentarios.
Ejemplo 1
En este ejemplo veremos cuánto es la derivada del arcocotangente de la función cuadrática x2.
En el argumento del arcocotangente tenemos una función distinta a x, por lo que debemos aplicar la fórmula de la derivada del arcocotangente junto con la regla de la cadena:
La derivada de x elevada a la dos es 2x, así que en el numerador tenemos que poner 2x y en el denominador la función del argumento al cuadrado:
Ejemplo 2
En este segundo ejemplo derivaremos el arcocotangente de una función polinómica de tercer grado.
Utilizamos la regla de la derivada del arcocotangente para hacer su derivación:
De manera que la derivada del arcocotangente de la función es:

