▷ Derivada de la tangente hiperbólica (fórmula y ejemplos)

Aquí encontrarás cuál es la derivada de la tangente hiperbólica de una función. Además, podrás ver varios ejemplos resueltos de derivadas de tangentes hiperbólicas. Y, por último, te demostramos la fórmula de la derivada de la tangente hiperbólica.

Índice

Fórmula de la derivada de la tangente hiperbólica

La derivada de la tangente hiperbólica de x es igual a 1 partido por el cuadrado del coseno hiperbólico de x. La derivada de la tangente de x también es equivalente al cuadrado de la secante hiperbólica de x, y a 1 menos el cuadrado de la tangente hiperbólica de x.

$\begin{array}{c}f(x)=\text{tanh}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=\text{sech}^2(x)=1-\text{tanh}^2(x)\end{array}$

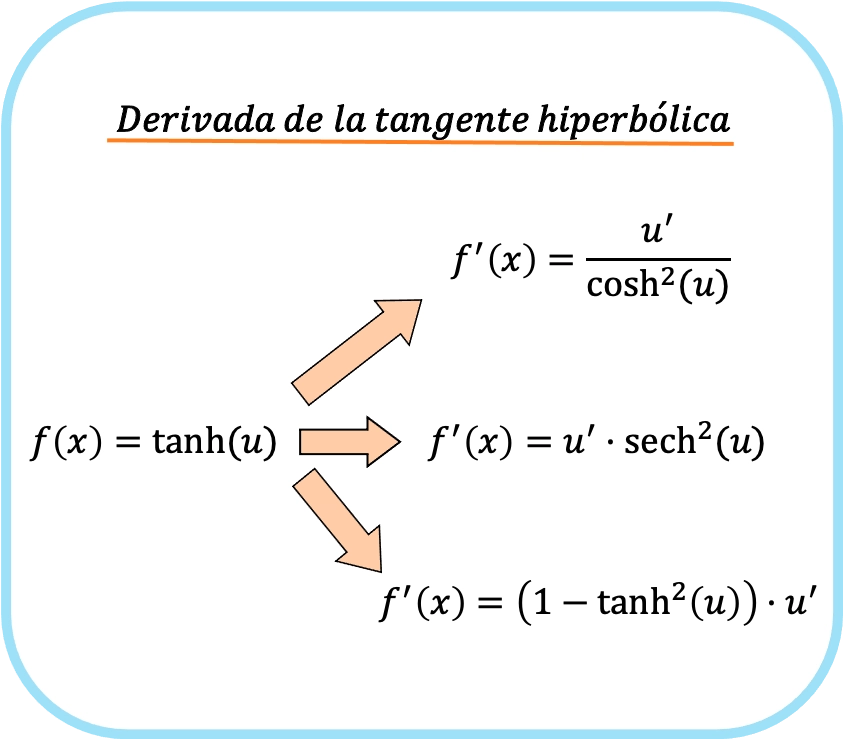
Por otro lado, si en el argumento de la función tenemos una función diferente de x, debemos aplicar la regla de la cadena. Y entonces las tres fórmulas de la derivada de la tangente hiperbólica son:

$\begin{array}{c}f(x)=\text{tanh}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cosh}^2(u)}=\text{sech}^2(u)\cdot u'=\left(1-\text{tanh}^2(u)\right)\cdot u'\end{array}$

Esto no significa que cada vez que derivemos la tangente hiperbólica tengamos que usar las tres fórmulas, sino que podemos utilizar cualquiera de ellas para derivarla. Así pues, según como sea la función del argumento de la tangente hiperbólica, será mejor utilizar una fórmula u otra. Más abajo tienes varios ejemplos en los que puedes ver cómo se deriva la tangente hiperbólica de una función.

La derivada de la tangente hiperbólica es casi idéntica a la derivada de la tangente, pero tiene un pequeño detalle que las hace totalmente diferente. Puedes ver cuál es la diferencia en el siguiente enlace:

➤ Ver: fórmula de la derivada de la tangente

Ejemplos de la derivada de la tangente hiperbólica

Vista cuál es la fórmula de la derivada de la tangente hiperbólica, a continuación tienes varios ejemplos resueltos de derivadas de este tipo de funciones trigonométricas para que entiendas perfectamente cómo derivar la tangente hiperbólica.

Ejemplo 1: Derivada de la tangente hiperbólica de 2x

$f(x)=\text{tanh}(2x)$

Para derivar la tangente hiperbólica de este ejemplo utilizaremos la fórmula del coseno hiperbólico, aunque evidentemente puedes utilizar la que prefieras.

$f(x)=\text{tanh}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cosh}^2(u)}$

Sabemos que la derivada de 2x es 2, por lo tanto, la derivada de toda la función es:

$f(x)=\text{tanh}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\text{cosh}^2(2x)}$

Ejemplo 2: Derivada de la tangente hiperbólica de x al cuadrado

$f(x)=\text{tanh}(x^2)$

La regla de la derivada de la tangente hiperbólica de una función es:

$f(x)=\text{tanh}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cosh}^2(u)}$

Por un lado derivamos la función del argumento x², que da 2x, y después resolvemos la derivada de toda la función utilizando la fórmula:

$f(x)=\text{tanh}(x^2)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\text{cosh}^2(x^2)}$

Ejemplo 3: Derivada de la tangente hiperbólica al cubo

$f(x)=\text{tanh}^3(7x^2)$

En este caso debemos derivar la tangente hiperbólica de una función que, además, está elevada a una potencia. De modo que debemos usar la fórmula de la derivada de una función potencial, la regla de la derivada de la tangente hiperbólica y la regla de la cadena:

$f'(x)=3\text{tanh}^2(7x^2)\cdot \cfrac{14x}{\text{cosh}^2(7x^2)}}=\cfrac{42x\cdot \text{tanh}^2(7x^2)}{\text{cosh}^2(7x^2)}}$

Demostración de la derivada de la tangente

En este apartado demostraremos la fórmula de la derivada de la tangente hiperbólica. Y, para ello, partiremos de la identidad trigonométrica que relaciona las tres razones trigonométricas hiperbólicas:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

➤ Nota: Para entender la demostración debes saber cuál es la derivada de seno hiperbólico y cuál es la derivada del coseno hiperbólico. Por eso te recomendamos que visites las páginas enlazadas antes de seguir.

Ahora aplicamos la fórmula de la derivada de un cociente:

$\displaystyle\left(\text{tanh}(x)\right)'=\left(\frac{\text{senh}(x)}{\text{cosh}(x)}\right)'$

$\text{tanh}'(x)=\cfrac{\text{cosh}(x)\cdot \text{cosh}(x)-\text{senh}(x)\text{senh}(x) }{\text{cosh}^2(x)}$

$\text{tanh}'(x)=\cfrac{\text{cosh}^2(x)-\text{senh}^2(x)}{\text{cosh}^2(x)}$

Reducimos la expresión del numerador de la fracción utilizando la siguiente fórmula:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

$\text{tanh}'(x)=\cfrac{1}{\text{cosh}^2(x)}$

Como puedes ver, la igualdad anterior corresponde a la primera fórmula de la derivada de la tangente hiperbólica. Asimismo, la secante hiperbólica es el inverso multiplicativo del coseno hiperbólico, de manera que también se demuestra la segunda fórmula:

$\text{tanh}'(x)=\text{sech}^2(x)$

Finalmente, podemos llegar a la tercera regla de la derivada de la tangente hiperbólica convirtiendo la fracción del paso anterior en una resta de fracciones:

$\text{tan}'(x)=\cfrac{\text{cosh}^2(x)-\text{senh}^2(x)}{\text{cosh}^2(x)}$

$\text{tanh}'(x)=\cfrac{\text{cosh}^2(x)}{\text{cosh}^2(x)}-\cfrac{\text{senh}^2(x)}{\text{cosh}^2(x)}$

$\text{tanh}'(x)=1-\text{tanh}^2(x)$