Aquí encontrarás cómo se deriva la función tangente. Además, podrás ver ejemplos de la derivada de la tangente e incluso practicar con ejercicios resueltos paso a paso. Finalmente, también te demostramos la fórmula de la derivada de la tangente y te mostramos la fórmula de la derivada de la tangente inversa.
Índice
¿Cuál es la derivada de la tangente?
La derivada de la tangente de x es igual a 1 partido por el cuadrado del coseno de x. La derivada de la tangente de x también es equivalente al cuadrado de la secante de x, y a 1 más el cuadrado de la tangente de x.
Todas las expresiones son equivalentes, así que la función tangente tiene tres posibles fórmulas para hacer su derivación.
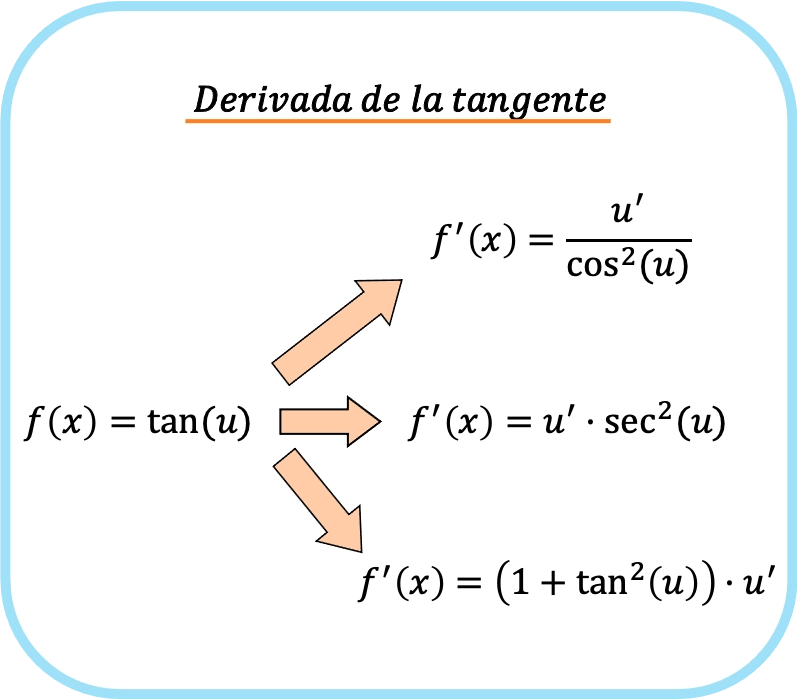
Por otro lado, cuando en el argumento de la tangente tenemos una función diferente de x (llamémosle u), debemos aplicar la regla de la cadena. De manera que la derivada de la tangente de u es:
En definitiva, la regla de la derivada de la tangente se puede resumir en:
Ejemplos de la derivada de la tangente
Vista la fórmula de la derivada de la tangente, en este apartado vamos a resolver varios ejemplos de este tipo de derivadas trigonométricas con el objetivo de que comprendas cómo derivar la función tangente.
Ejemplo 1: Derivada de la tangente de 2x
Para hacer la derivada de la tangente, puedes utilizar cualquiera de las tres fórmulas que hemos visto más arriba. Nosotros en este caso emplearemos la fórmula del coseno:
La función 2x és lineal, por lo que su derivada es 2. De modo que la derivada de la tangente de 2x es 2 partido por el cuadrado del coseno de 2x:
Ejemplo 2: Derivada de la tangente de x al cuadrado
En este ejemplo la función del argumento de la tangente no es una x, sino que es una función con derivada. Lo que significa que debemos aplicar la regla de la cadena para derivarla.
La derivada de x al cuadrado es 2x, así que la derivada de la tangente de x2 es:
Ejemplo 3: Derivada de la tangente al cubo
En este problema tenemos una función compuesta, por lo que también deberemos usar la regla de la cadena para derivar la tangente.
Además, la tangente está elevada a la 3, lo que significa que antes de aplicar la fórmula de la derivada de la tangente debemos utilizar la fórmula de la derivada de una potencia:
Derivada de la tangente inversa
Como toda función inversa, la función tangente también posee inversa, la función arcotangente. Aunque la fórmula para derivarla no se parece a la fórmula de la tangente, te la mostramos ya que puede resultarte útil en algunos casos.
La derivada de la tangente inversa de una función es el cociente de la derivada de la función dividida entre uno más dicha función al cuadrado
Por ejemplo, la derivada de la tangente inversa de 3x es la siguiente:
Ejercicios resueltos de la derivada de la tangente
Calcula la derivada de las siguientes funciones tangente:
Demostración de la derivada de la tangente
Para que puedas comprobar que no es una expresión inventada, en este apartado demostraremos la fórmula de la derivada de la tangente utilizando la definición matemática de la tangente.
Para ello, partiremos de la identidad trigonométrica que relaciona las tres razones trigonométricas:
Si utilizamos la fórmula de la derivada de una división, la derivada sería:
Pero, utilizando la identidad trigonométrica fundamental, sabemos que el cuadrado del seno más el cuadrado del coseno es 1:
Y de esta forma ya hemos llegado a la primera fórmula de la derivada de la tangente. Además, la secante es el inverso multiplicativo del coseno, por lo que la segunda expresión también queda demostrada:
Por último, se puede demostrar la tercera regla de la derivada de la tangente transformando la fracción del paso anterior en una suma de fracciones:

