Aquí encontrarás cómo derivar el seno hiperbólico (fórmula). Además, podrás ver varios ejemplos resueltos de la derivada del seno hiperbólico. Y, por último, demostramos la fórmula de la derivada de este tipo de función trigonométrica.
Índice
Fórmula de la derivada del seno hiperbólico
La derivada del seno hiperbólico de x es el coseno hiperbólico de x.
Por lo tanto, la derivada del seno hiperbólico de una función es igual al producto del coseno hiperbólico de la función por la derivada de esa función.
En realidad las dos fórmulas de arriba son la misma, la única diferencia es que en la segunda fórmula estamos aplicando la regla de la cadena. Y como la derivada de x es 1, esta no modifica la función.
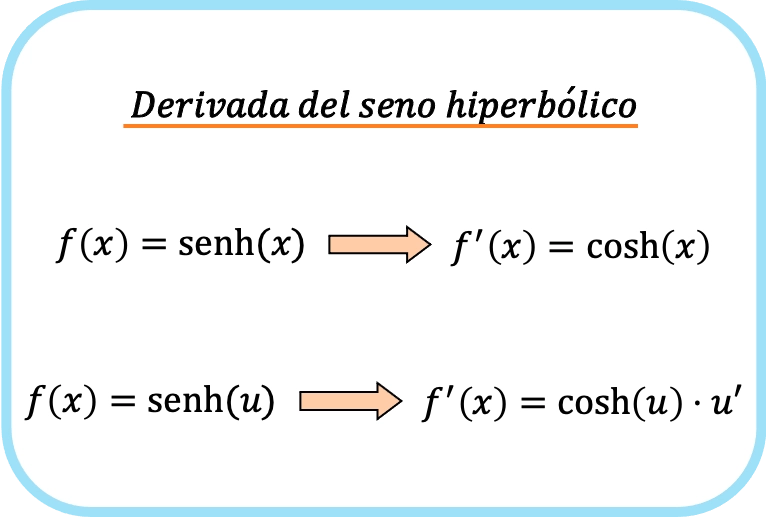
Como puedes ver, la fórmula de la derivada del seno hiperbólico es muy parecida a la fórmula de la derivada del seno.
Ejemplos de la derivada del seno hiperbólico
Una vez ya hemos visto cuál es la fórmula de la derivada del seno hiperbólico, pasamos ahora a resolver varios ejemplos de la derivada del seno hiperbólico. Así seguro que no te queda ninguna duda de cómo se hace.
Ejemplo 1: Derivada del seno hiperbólico de 2x
En este caso, en el argumento del seno hiperbólico tenemos una función diferente de x, por lo tanto, debemos utilizar la fórmula de la derivada del seno hiperbólico con la regla de la cadena para hallar la derivada:
La derivada de 2x es 2, así que la derivada del seno hiperbólico de 2x será el coseno hiperbólico de 2x multiplicado por 2.
Ejemplo 2: Derivada del seno hiperbólico de x al cuadrado
La fórmula de la derivada de la función seno hiperbólico es:
Por otro lado, la derivada de la función cuadrática x2 es 2x. De modo que la derivada de toda la función es:
Demostración de la fórmula de la derivada del seno hiperbólico
Finalmente, vamos a demostrar la fórmula de la derivada del seno hiperbólico. Para ello, partiremos de la definición matemática del seno hiperbólico:
Ahora derivamos los dos lados de la igualdad:
Para derivar el miembro derecho de la ecuación, utilizaremos la fórmula de la derivada de una división:
➤ Ver: derivada de la función exponencial de base e
Y precisamente hemos llegado a la expresión que define el coseno hiperbólico. De modo que queda demostrada la derivada del seno hiperbólico:
