En este post encontrarás cómo derivar el arcotangente de una función. Además, podrás ver ejemplos de este tipo de derivadas e, incluso, practicar con ejercicios resueltos de la derivada del arcotangente. Finalmente, también te enseñamos la demostración de la fórmula de la derivada del arcotangente.
Índice
¿Cuál es la derivada del arcotangente?
La derivada del arcotangente de x es uno partido por uno más x al cuadrado.
Por lo tanto, la derivada del arcotangente de una función es igual al cociente de la derivada de esa función partido por uno más dicha función al cuadrado.
En este caso, se ha representado la función como una u, por lo que sería la fórmula de la derivada del arcotangente de la función u.
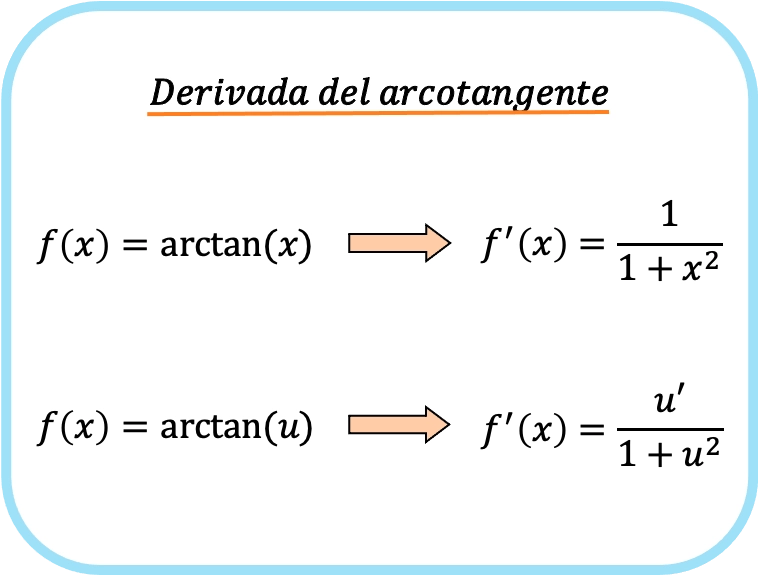
Como puedes comprobar, la fórmula de la derivada de la tangente inversa es muy parecida a las fórmulas de las derivadas del arcoseno y del arcocoseno.
Ejemplos de la derivada del arcotangente
Una vez sabemos cuál es la fórmula de la derivada del arcotangente, vamos a explicar la derivación de varios ejemplos de este tipo de derivadas trigonométricas. De esta forma te resultará más sencillo comprender cómo se deriva el arcotangente de una función.
Ejemplo 1: Derivada del arcotangente de 2x
Aplicamos la fórmula para resolver la derivada:
La derivada de 2x es 2, por lo tanto, la derivada del arcotangente de 2x es 2 entre uno más 2x al cuadrado:
Ejemplo 2: Derivada del arcotangente de x al cuadrado
Para hallar el resultado de la derivada de este ejemplo tenemos que utilizar la fórmula de la derivada del arcotangente, que es:
Así pues, la derivada de la función x2 es 2x, por lo que la derivada del arcotangente de x elevada a la 2 es:
Ejemplo 3: Derivada del arcotangente del seno de x
Lógicamente, para calcular la derivada debemos aplicar su fórmula correspondiente:
En este caso tenemos una función compuesta, así que debemos aplicar la regla de la cadena para calcular la derivada del arcotangente:
Ejercicios resueltos de la derivada del arcotangente
Deriva las siguientes funciones arcotangente:
Demostración de la fórmula de la derivada del arcotangente
A continuación, vamos a demostrar la fórmula de la derivada del arcotangente.
Primero pasamos el arcotangente a tangente aprovechando que el arcotangente es la función inversa de la tangente:
Derivamos en los dos lados de la ecuación:
Despejamos y’:
Por otro lado, gracias a la identidad trigonométrica fundamental sabemos que la suma de los cuadrados del seno y del coseno es igual a 1. Por tanto, podemos transformar la expresión anterior en una fracción:
Dividimos todos los términos entre el cuadrado del coseno:
El seno entre el coseno es igual a la tangente, por tanto:
Tal y como hemos visto arriba, la tangente es equivalente a la variable x, por lo que podemos sustituir la expresión para llegar a la fórmula de la derivada del arcotangente:
