En este post encontrarás la definición del teorema de Weierstrass. Además, podrás practicar con varios ejercicios resueltos paso a paso del teorema de Weierstrass para entenderlo perfectamente.
Índice
Enunciado del teorema de Weierstrass
El teorema de Weierstrass dice que si una función es continua en un intervalo cerrado, dicha función tiene un máximo absoluto y un mínimo absoluto en ese intervalo.
➤ Ver: ¿Qué es una función continua?
El teorema de Weierstrass solamente establece que existe un máximo y un mínimo, pero no sirve para calcular los valores de esos puntos.
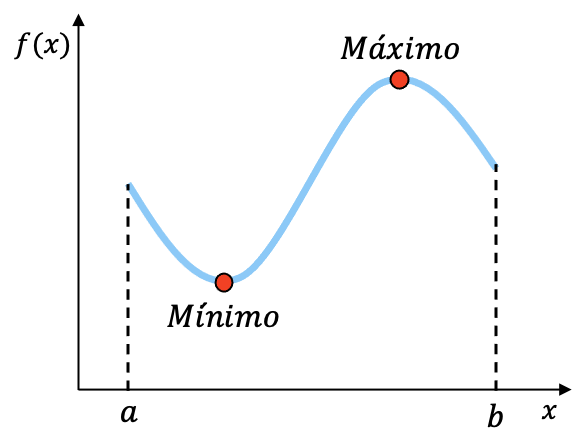
Por ejemplo, la función representada gráficamente arriba es continua en el intervalo [a,b] y tiene un mínimo y un máximo en ese intervalo. Aunque no podemos conocer con exactitud las coordenadas de esos dos puntos, sí que sabemos que la función tiene esos dos extremos dentro del intervalo.
➤ Ver: cómo calcular los máximos y mínimos de una función
Como la función es continua en todo el intervalo, significa que también tomará todos los valores posibles entre el mínimo absoluto y el máximo absoluto en ese mismo intervalo.
Además, como consecuencia del teorema de Weierstrass, se puede deducir que toda función continua en un intervalo cerrado está acotada superiormente e inferiormente, y la cota superior e inferior de la función son el máximo y el mínimo absoluto respectivamente.
Matemáticamente, el teorema de Weierstrass se puede expresar de la siguiente manera:
Donde 
y 
son dos puntos comprendidos (el mínimo absoluto y el máximo absoluto respectivamente) dentro del intervalo cerrado ![[a,b]](https://www.funciones.xyz/wp-content/ql-cache/quicklatex.com-f319a9db7e6ffb41ac9e2065d84cb28f_l3.svg "Rendered by QuickLaTeX.com")
en el que está definida la función.
La demostración del teorema de Weierstrass es bastante complicada y no aporta demasiado al concepto, así que no la explicaremos en este post. Lo importante es que entiendas qué es y para qué sirve el teorema de Weierstrass.
Ejercicios resueltos del teorema de Weierstrass
Ejercicio 1
Determina si la siguiente función está acotada en el intervalo propuesto:
![f(x)=\log_3(x-4) \qquad x \in [5,10]](https://www.funciones.xyz/wp-content/ql-cache/quicklatex.com-351ade51baf24385c9334acb7018ab05_l3.svg "Rendered by QuickLaTeX.com")
➤ Ver: dominio de una función logarítmica
Podemos determinar si la función está acotada en el intervalo [5,10] aplicando el teorema de Weierstrass. De manera que debemos averiguar si la función es continua en este intervalo, para ello, calculamos el dominio de la función logarítmica:
La función es continua para todos los valores mayores que x=4, por lo tanto, es continua en el intervalo [5,10].
En consecuencia, la función cumple con el teorema de Weierstrass en el intervalo [5,10], lo que significa que está acotada superior e inferiormente en ese intervalo.
Ejercicio 2
Determina si la siguiente función tiene un máximo y/o un mínimo en el intervalo propuesto:
![f(x)=\cfrac{3x^2-4}{2x-4} \qquad x \in [-3,3]](https://www.funciones.xyz/wp-content/ql-cache/quicklatex.com-873703e5de7dce2e8624e75ae228b589_l3.svg "Rendered by QuickLaTeX.com")
➤ Ver: dominio de una función racional
En primer lugar, analizamos la continuidad de la función racional:
Sin embargo, la función tiene una discontinuidad en x=2, lo que implica que no es continua en el intervalo [-3,3].
En definitiva, la función no cumple el teorema de Weierstrass y por tanto no podemos afirmar si tiene un mínimo o un máximo en este intervalo.
Ejercicio 3
Determina si la siguiente función tiene un máximo y/o un mínimo en el intervalo propuesto y calcula dichos puntos:
![f(x)=x^2+3 \qquad x \in [0,4]](https://www.funciones.xyz/wp-content/ql-cache/quicklatex.com-cf95845b16297e1db10c2fdd76882d69_l3.svg "Rendered by QuickLaTeX.com")
➤ Ver: características de las funciones cuadraticas
El dominio de cualquier función cuadrática son todos los números reales:
De modo que la función es continua en el intervalo [0,4] y verifica el teorema de Weierstrass. Así que la función tiene un mínimo absoluto y un máximo absoluto en este intervalo.
Además, el vértice de esta parábola está justo en x=0, por lo tanto, la función es estrictamente creciente en el intervalo [0,4] y, en consecuencia, el mínimo se encuentra en x=0 y el máximo en x=4.
Karl Weierstrass
Una vez hemos visto qué significa el teorema de Weierstrass, vamos a explicar brevemente quién fue el inventor de este teorema.
Karl Theodor Wilhelm Weierstrass fue una matemático alemán muy importante en el siglo XIX, en concreto, nació el 31 de octubre de 1815 en Ostenfelde y murió el 19 de febrero de 1897 en Berlín.
Además del teorema de Weierstrass, también se lo conoce por hacer otras contribuciones a las matemáticas. Entre ellas, dio las definiciones de continuidad, límite y derivada, tres conceptos muy importantes de las funciones.
Asimismo, logró demostrar algunos teoremas que por aquel entonces aún no estaban matemáticamente verificados, como el teorema de Bolzano-Weierstrass, el teorema del valor medio o el teorema de Heine-Borel.
Como curiosidad, hay un cráter lunar i un asteroide que llevan el nombre de Weierstrass en su honor.
