Función racional

Aquí encontrarás qué son las funciones racionales. Además, te explicamos cómo calcular el dominio y las asíntotas de una función racional. Y no solo eso, sinó que verás cuáles son todas las características de las funciones racionales. Por último, podrás practicar con ejercicios resueltos paso a paso de las funciones racionales.

¿Qué es una función racional?

La definición de función racional es la siguiente:

Una función racional es aquella función formada por el cociente de dos polinomios, es decir, una función racional es una fracción que tiene un polinomio en el numerador y en el denominador.

Las funciones racionales se caracterizan por tener singularidades en aquellos puntos en los que se anula el denominador.

f(x)=\cfrac{a_0+a_1x+a_2x^2+\dots +a_nx^n}{b_0+b_1x+b_2x^2+\dots +n_nx^n}

Las funciones racionales también se conocen como funciones fraccionarias.

Por otro lado, no se deben confundir las funciones racionales con las funciones irracionales. Las funciones irracionales (o radicales) son aquellas que están formadas por raíces.

Ejemplos de funciones racionales

Para entender mejor el concepto de función racional, vamos a ver varios ejemplos de este tipo de función.

  • Función racional con un polinomio de primer grado en el numerador y en el denominador:

f(x)=\cfrac{x+3}{2x-5}

Este tipo de funciones racionales también se llaman funciones homográficas.

  • Función racional con una constante en el numerador y un polinomio en el denominador:

f(x)=\cfrac{7}{x+1}

Este tipo de funciones racionales se conocen como funciones de proporcionalidad inversa, y se utilizan para definir matemáticamente magnitudes que son inversamente proporcionales.

  • Función racional con un polinomio de tercer grado en el numerador y un polinomio de segundo grado en el denominador:

f(x)=\cfrac{x^3+4x^2-2x+6}{x^2+3x-1}

Dominio de una función racional

Un número dividido entre 0 es una indeterminación que da como resultado infinito (∞), así que una función racional existirá siempre menos cuando el denominador sea 0.

Por lo tanto, el dominio de una función racional son todos los números reales excepto aquellos valores que anulan el denominador.

Entonces, para sacar el dominio de una función racional debemos encontrar cuándo el denominador es 0, ya que ese punto será el único que no pertenece al dominio

Veamos cómo se calcula el dominio de una función racional resolviendo un ejemplo:

f(x)=\cfrac{5x}{x+2}

Primero igualamos el denominador a 0, y luego resolvemos la ecuación resultante:

x+2=0

x=-2

Por tanto, cuando x sea -2 el denominador será 0 y, en consecuencia, la función no existirá. Así que el domino de la función son todos los números reales menos x=-2. Esto se indica de la siguiente manera:

\text{Dom } f= \mathbb{R}-\{ -2 \}

Asíntotas de una función racional

Una de las propiedades principales de las funciones racionales son sus asíntotas, ya que determinan su representación gráfica.

➤ Ver: representación gráfica de una función

Las asíntotas de una función racional son rectas a la cual la gráfica de la función se va acercando indefinidamente pero nunca llega a tocarlas.

Existen tres tipos de asíntotas: las asíntotas verticales, las asíntotas horizontales y las asíntotas oblicuas.

A continuación, tienes representadas gráficamente de color rojo los tres tipos de asíntotas que puede tener una función racional.

Asíntota vertical de una función racional

asíntota vertical de una funcion racional

 

Asíntota horizontal de una función racional

asíntota horizontal de una funcion racional

 

Asíntota oblicua de una función racional

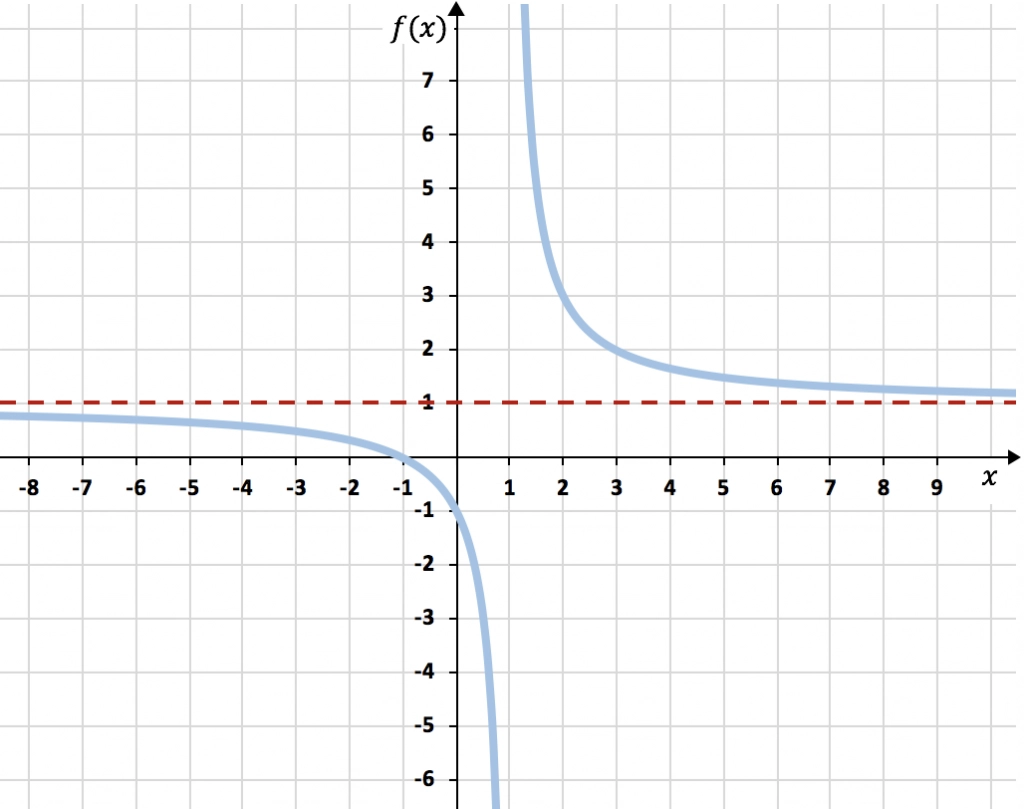
asíntota oblicua de una funcion racional

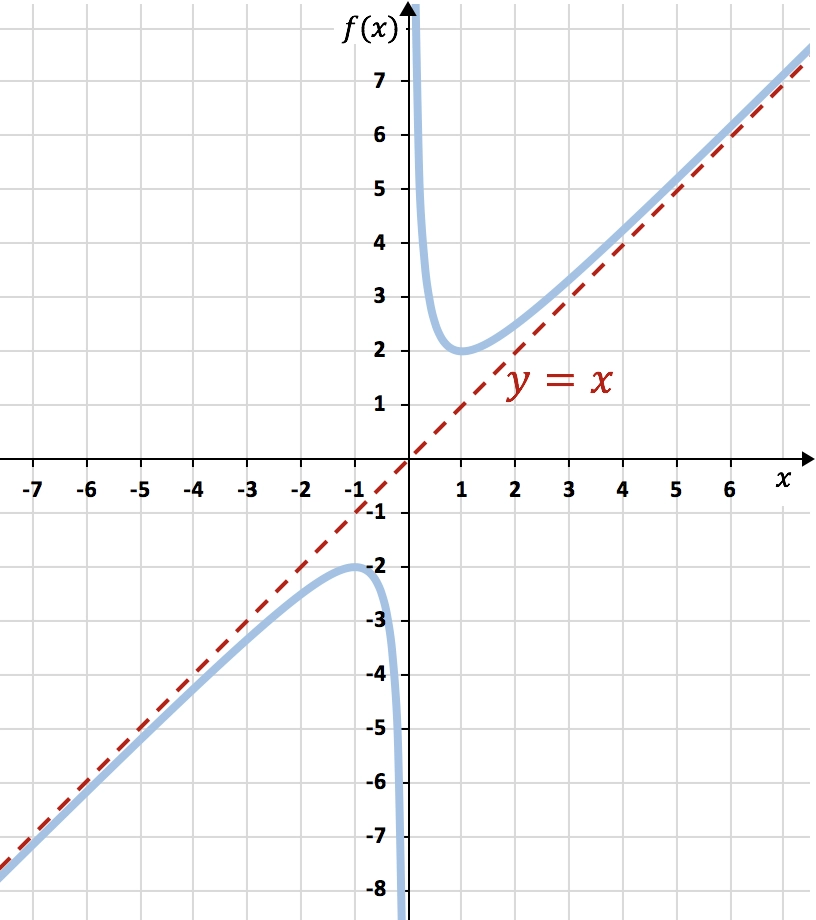
Como puedes ver, determinar la asíntota de una función a partir de su gráfica es bastante fácil, pero calcular las asíntotas de una función racional sin tener su representación gráfica es bastante complicado. Por eso te recomendamos que veas cómo se calculan las asíntotas de una función en nuestra web.

Características de una función racional

Las funciones racionales tienen las siguientes características:

f(x)=\cfrac{P(x)}{Q(x)}

  • Como hemos visto más arriba, el dominio de las funciones racionales son todos los números reales excepto aquellos valores que anulan el denominador de la fracción.
  • En general, el recorrido (o rango) de una función racional son todos los números reales menos aquellos valores en los que la función posee una asíntota horizontal.
  • Las funciones racionales son continuas en todo su dominio. O en otras palabras, las funciones racionales presentan discontinuidades en los puntos que no pertenecen a su dominio.
  • La representación gráfica de la mayoría de funciones racionales son dos hipérbolas.
  • Se pueden deducir algunas reglas de las asíntotas de las funciones racionales a partir del polinomio del numerador P(x) y el polinomio del denominador Q(x):
    • Una función racional tiene una asíntota vertical en los puntos que son raíces de Q(x) pero que no son raíces de P(x).
    • Si el grado de P(x) es menor que el grado de Q(x), la recta y=0 es una asíntota horizontal de la función racional.
    • Si el grado de P(x) es mayor que el grado de Q(x), la función racional no tiene asíntota horizontal.
    • Si el grado de P(x) es una unidad mayor que el grado de Q(x) y los dos polinomios no tienen ninguna raíz en común, la función racional tiene una asíntota oblicua.

Ejercicios resueltos de funciones racionales

Ejercicio 1

Halla el dominio de la siguiente función racional:

f(x)=\displaystyle\frac{4x}{2x+4}

Se rata de una función racional, por tanto, el dominio son todos los números menos los que anulan el denominador, ya que entonces la función daría ∞.

Así que igualamos a cero todo el denominador para ver qué número no pertenece al dominio:

2x+4=0

Y resolvemos la ecuación resultante:

2x=-4

x=\cfrac{-4}{2}=-2

De modo que el dominio de la función son todos los números excepto el -2:

\mathbf{Dom } \ \bm{f = \mathbb{R}- \{ -2 \} }

 

Ejercicio 2

Encuentra los puntos de corte de la siguiente función racional con los ejes cartesianos:

f(x)=\cfrac{x^2-9}{x}

Punto de corte con el eje X

Para encontrar el punto de corte de la función con el eje X debemos resolver f(x)=0:

f(x)=0

\cfrac{x^2-9}{x}=0

x^2-9=0\cdot x

x^2-9=0

x^2=9

x^2=\pm 3

Hemos obtenido dos soluciones de la ecuación de segundo grado, por tanto, la función racional corta con el eje de las abscisas en dos puntos distintos, que son:

\bm{(3,0)\qquad (-3,0)}

Punto de corte con el eje Y

Para hallar el punto de corte con el eje Y debemos calcular f(0):

f(0)=\cfrac{0^2-9}{0}=\cfrac{-9}{0}= \infty

Cualquier número dividido entre cero es una indeterminación que da como resultado infinito. Por lo tanto, la función racional no pasa por encima del eje Y en ningún punto, es decir, no tiene ningún punto de corte con el eje de las ordenadas.

 

Ejercicio 3

Representa en una gráfica la siguiente función racional:

y=\cfrac{2x+3}{2x+6}

Lo primero que debemos hacer es calcular el dominio de la función:

2x+6=0

2x =-6

x =\cfrac{-6}{2} =-3

\text{Dom } f = \mathbb{R} - \{ -3 \}

Una vez conocemos el dominio de la función, construimos una tabla de valores:

\begin{array}{c|c} x & y \\ \hline -2,5 & -2 \\ -2 & -0,5 \\ -1 & 0,25 \\ 1 & 0,63 \\ -3,5 & 4 \\ -4 & 2,5 \\ -5 & 1,75 \\ -7 & 1,38\end{array}

Para acabar, solo nos falta representar los puntos obtenidos en una gráfica y trazar las hipérbolas, dibujando así la función racional:

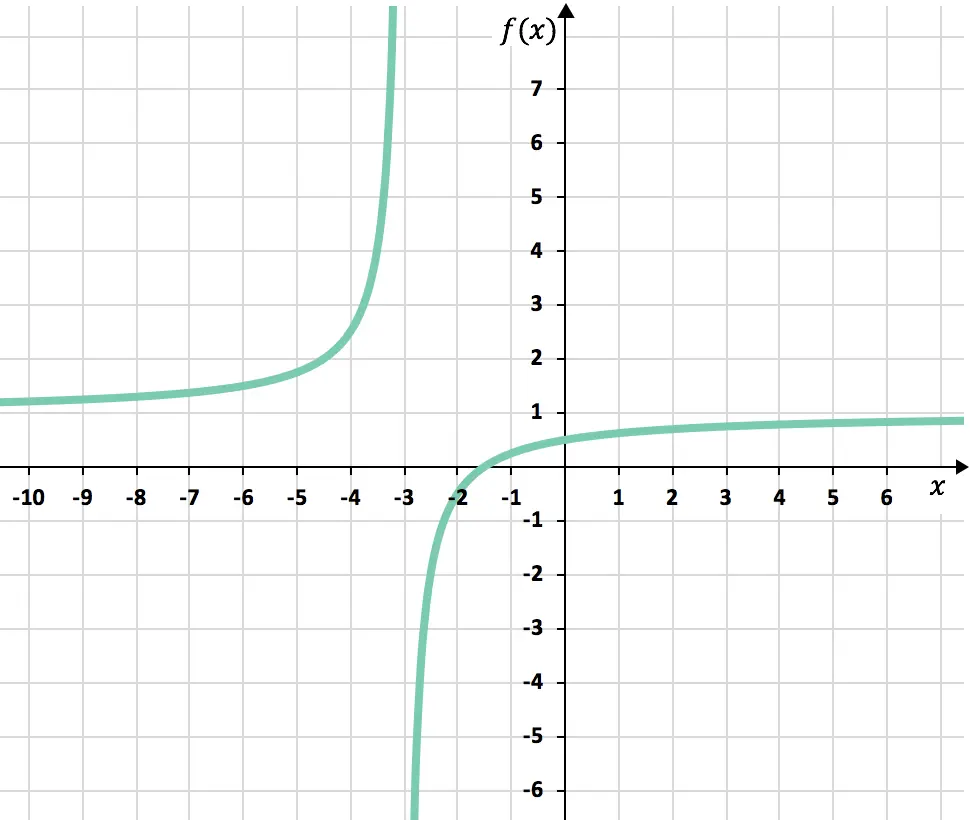
funcion de proporcionalidad inversa

 

Ejercicio 4

Determina las asíntotas de la función racional representada gráficamente a continuación:

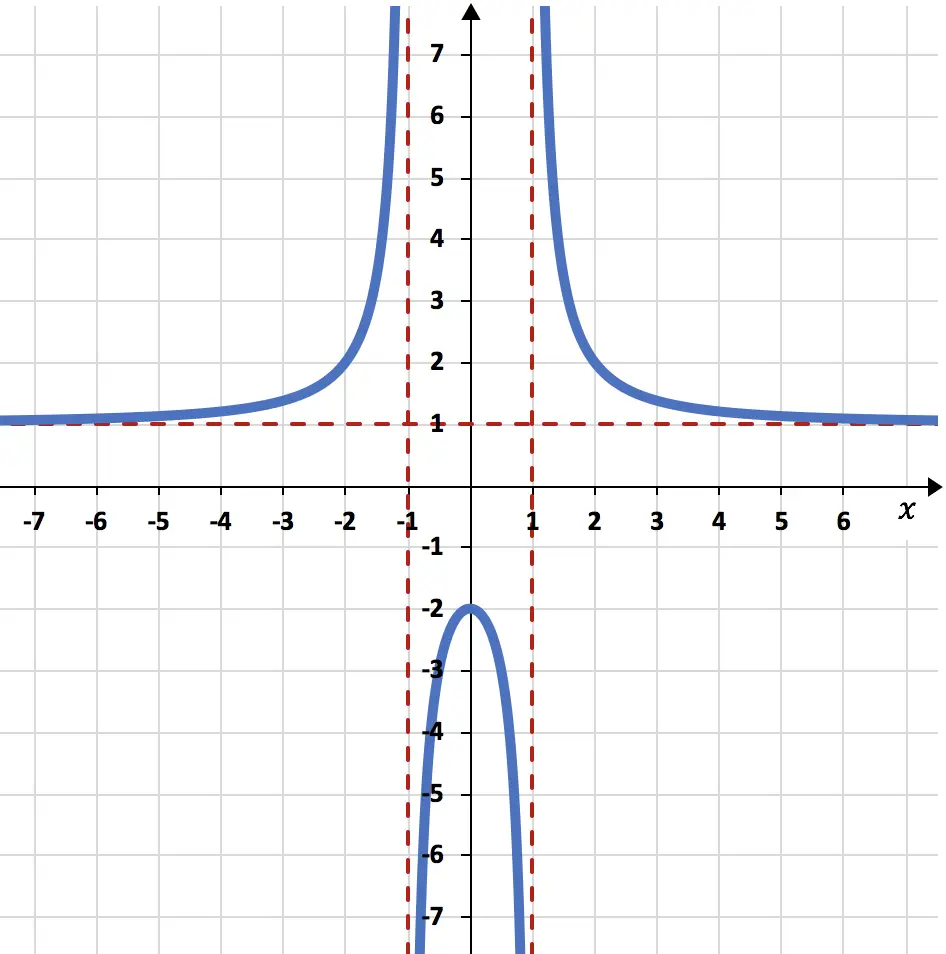
asíntotas de una función racional

Las asíntotas se aprecian muy bien en la gráfica, ya que está representadas en forma de rectas discontinuas de color rojo.

En este problema, la función se aproxima mucho a la recta horizontal y=1 pero nunca llega a tocarla. Por tanto, la función racional tiene una única asíntota horizontal, que es y=1.

Del mismo modo, la representación gráfica de la función se acerca mucho a las rectas verticales x=-1 y x=1, pero nunca llega a alcanzar dichos valores. Así que la función racional tiene dos asíntotas verticales diferentes, que son x=-1 y x=1.

 

Ejercicio 5

Calcula todas las asíntotas de la siguiente función racional:

\displaystyle f(x)=\frac{6x-4}{2x+2}

Nota: para resolver este ejercicio te recomendamos que antes vayas al enlace que hay más arriba de cómo se calculan las asíntotas de una función y veas la explicación.

Asíntota vertical

Para calcular las asíntotas verticales de una función, primero debemos hallar el dominio de la función. Por tanto, igualamos el denominador de la función racional a 0 para encontrar los puntos que no pertenecen al dominio:

2x +2 =0

2x= -2

x = \cfrac{-2}{2} = -1

De modo que el dominio de la función son todos los números menos el -1:

\text{Dom } f = \mathbb{R} - \left\{ -1 \right\}

Así que x=-1 podría ser una asíntota vertical. Para comprobarlo, tenemos que calcular el límite de la función en el punto:

\displaystyle \lim_{x \to -1 } \frac{6x-4}{2x+2} = \frac{6\cdot(-1)-4}{2\cdot(-1)+2}=\frac{-10}{0}= \infty

Por tanto, x=-1 es una asíntota vertical de la función racional, ya que el límite de la función en este punto da infinito.

Asíntota horizontal

Para determinar las asíntotas horizontales tenemos que calcular el límite al infinito de la función:

\displaystyle \lim_{x \to +\infty}\frac{6x-4}{2x+2} = \frac{6(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{6}{2} = \bm{3}

\displaystyle \lim_{x \to -\infty}\frac{6x-4}{2x+2} = \frac{6(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{6}{2} = \bm{3}

En este caso el resultado del límite indeterminado infinito entre infinito es la división de los coeficientes de las x de mayor grado, ya que el numerador y el denominador son del mismo orden.

Ambos límites al infinito de la función nos han dado 3, por tanto, y=3 es una asíntota horizontal de la función racional.

Asíntota oblicua

Como hay asíntota horizontal, la función racional no tiene asíntota oblicua.

 

12 comentarios en “Función racional”

  1. ARTURO

    SERIA BUENO QUE TERMINE CON UN ESTUDIO COMPLETO DE LA FUNCIÓN RACIONAL, COMO EL DOMINIO, RANGO, ASINTOTAS, MONOTONÍA Y GRÁFICA PERO ANALIZADO A TRAVÉS DE UN PROBLEMA

    Responder
    1. Funciones

      Hola Arturo, tienes este tipo de ejercicios resueltos paso a paso en el post de representación de funciones (tienes el enlace arriba). Te recomiendo que vayas a ese post y practiques con ellos.

  2. Robertb27

    Hola. Felicidades por tan excelente material didáctico. Quiero hacerles una observación en cuanto al comentario:

    «Un número dividido entre 0 es una indeterminación que da como resultado infinito (∞), así que una función racional existirá siempre menos cuando el denominador sea 0.»

    Creo que hay una confusión en el concepto. Todo número dividido entre cero (0) produce una INDEFINICIÓN MATEMÁTICA (∞), excepto el propio cero (0), que produce una INDETERMINACIÓN MATEMÁTICA. Son conceptos diferentes. Así 1/0 es INDEFINIDO (∞), pero 0/0 es INDETERMINADO (puede determinarse sus valores haciendo algunas operaciones matemáticas).
    Existen unas pocas indeterminaciones matemáticas (7), todo lo demás que no pueda ser resuelto en los números reales se considera una indefinición.
    Saludos y gracias.

    Responder
    1. Funciones

      Hola Robert,

      Efectivamente, tienes toda la razón. En este post no se ha profundizado este concepto porque no es el tema en cuestión, por eso se había simplificado para entender lo importante de este artículo.

      Tal y como comentas, existen diferentes indeterminaciones, están explicadas todas ellas en nuestro artículo sobre los tipos de indeterminaciones.

      ¡Muchas gracias por tu aportación!

    1. Funciones

      Hola Alejandro,

      Normalmente no se distinguen diferentes tipos de funciones racionales, ya que al final el procedimiento para representarlas gráficamente es el mismo.

      Si quieres, puedes clasificar las funciones racionales según el tipo de asíntota que tienen (arriba tienes explicadas los tres tipos de asíntotas que pueden tener).

    1. Funciones

      Hola Bella,

      Si la expresión racional no tiene ninguna incógnita, sino que es simplemente una fracción con un número en el numerador y otro número en el denominador, entonces no es una función racional. Además, lógicamente la función racional debe cumplir con todas las propiedades que define a una función.

    1. Funciones

      Hola Guido,

      Si lo que quieres averiguar es el dominio de la función racional, debes igualar el denominador de la fracción a cero y resolver la ecuación:

      x-2=0

      x=2

      De modo que el dominio de la función racional son todos los números reales excepto x=2.

      \text{Dom } f= \mathbb{R}-\{ 2 \}

  6. Micaela

    Es maravilloso el material que hay en esta página, muchísimas gracias! son unos genios. Tienen alguna página que se dedique a integrales nomás?

    Responder
    1. Funciones

      ¡Muchísimas gracias Micaela!

      No de momento no, ¡pero ya está pensado ampliar el temario de este sitio web y añadir toda la teoría de las integrales en un futuro!

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *