Máximos y mínimos de una función (extremos relativos)

En este post encontrarás cómo calcular los máximos y mínimos de una función, te lo explicamos resolviendo dos ejemplos paso a paso. Además, podrás practicar con ejercicios resueltos paso a paso de los máximos y mínimos de una función.

¿Qué son los máximos y mínimos de una función?

Los máximos de una función son los valores más grandes de la función y los mínimos de una función son los valores más pequeños de la función. Los máximos y mínimos de una función son extremos relativos cuando solo son los valores más grandes o más pequeños de su entorno, pero son extremos absolutos cuando son los valores más grandes o más pequeños de toda la función.

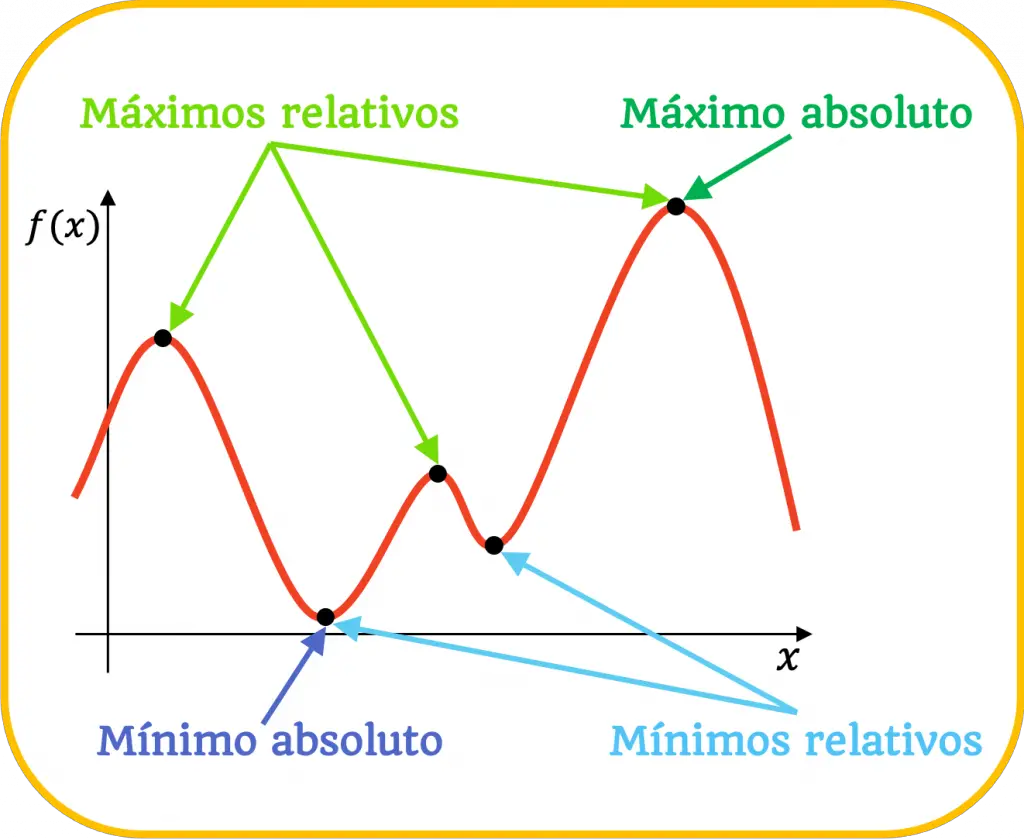
maximos y minimos de una funcion

También se pueden identificar los extremos relativos estudiando el crecimiento y decrecimiento de la función:

  • Un punto es un máximo relativo cuando la función pasa de ser creciente a ser decreciente.
  • Un punto es un mínimo relativo cuando la función pasa de ser decreciente a ser creciente.

Cómo hallar los máximos y mínimos de una función

A partir de la primera y segunda derivada de una función, se puede saber si una función tiene un extremo relativo en un punto y si dicho punto es un máximo relativo o un mínimo relativo:

  • Una función tiene un extremo relativo en los puntos que anulan su primera derivada.

    • f'(a)=0 \quad \bm{\longrightarrow} \quad x=a \text{ es un extremo relativo}

  • Y el signo de la segunda derivada de la función determina si el punto es un máximo o un mínimo:
    • Si la segunda derivada es negativa, la función tiene un máximo relativo en ese punto.

      • f''(a)<0 \quad \bm{\longrightarrow} \quad x=a \text{ es un m\'aximo relativo}

    • Si la segunda derivada es positiva, la función tiene un mínimo relativo en ese punto.

      • f''(a)>0 \quad \bm{\longrightarrow} \quad x=a \text{ es un m\'inimo relativo}

Ejemplo 1: Cómo calcular los máximos y mínimos de una función

Una vez hemos visto las definiciones de máximo y mínimo de una función, vamos a resolver un ejemplo paso a paso para que puedas ver cómo se calculan los máximos y los mínimos de una función.

  • Calcula los extremos relativos de la siguiente función y determina si son máximos o mínimos:

f(x)=x^3-3x

Los extremos relativos de la función serán aquellos puntos que cumplan f'(x)=0. Por tanto, primero calculamos la derivada de la función:

f(x)=x^3-3x \ \longrightarrow \ f'(x)=3x^2-3

Y ahora igualamos la derivada de la función a cero y resolvemos la ecuación cuadrática resultante:

f'(x)=0

3x^2-3=0

3x^2=3

x^2=\cfrac{3}{3}

x^2=1

x= \pm 1

Por tanto, los extremos relativos de la función son x=+1 y x=-1.

Una vez sabemos los extremos relativos de la función, podemos averiguar si son un máximo o un mínimo con el signo de la segunda derivada. Por lo que calculamos la segunda derivada de la función:

f'(x)=3x^2-3 \ \longrightarrow \ f''(x)=6x

Y ahora evaluamos en la segunda derivada los extremos relativos que hemos encontrado antes, para averiguar si son un máximo o un mínimo relativo:

f''(1)=6\cdot 1 = 6 \ \longrightarrow  Mínimo relativo

f''(-1)=6\cdot (-1) = -6 \ \longrightarrow  Máximo relativo

La segunda derivada en x=1 es positiva, por lo que x=1 es un mínimo relativo. En cambio, la segunda derivada en x=-1 es negativa, de modo que x=-1 es un máximo relativo.

Por último, sustituimos los puntos encontrados en la función original para hallar la coordenada Y de los extremos relativos:

f(1)=1^3-3\cdot 1=-2 \ \longrightarrow \ (1,-2)

f(-1)=(-1)^3-3\cdot(-1)= 2 \ \longrightarrow \ (-1,2)

En conclusión, los extremos relativos de la función son:

Mínimo en el punto \bm{(1,-2)}

Máximo en el punto \bm{(-1,2)}

Ejemplo 2: Estudiar la monotonía y los máximos y mínimos de una función

Ahora vamos a ver cómo se resuelve otro tipo de ejercicio. En este caso explicaremos cómo encontrar los máximos y mínimos a partir de la monotonía de una función.

  • Estudia la monotonía y calcula los extremos relativos de la siguiente función:

f(x)=\cfrac{x^2}{x-1}

Lo primero que debemos hacer es calcular el dominio de la función. Al ser una función racional, tenemos que igualar a 0 el denominador para ver qué números no pertenecen al dominio de la función:

x-1=0

x=1

\text{Dom } f= \mathbb{R}-\{1 \}

Una vez hemos calculado el dominio de la función, debemos estudiar qué puntos anulan la primera derivada. Así que derivamos la función:

f(x)=\cfrac{x^2}{x-1} \ \longrightarrow \ f'(x)= \cfrac{2x\cdot (x-1) - x^2\cdot 1}{\left(x-1\right)^2}

f'(x)=\cfrac{2x^2-2x - x^2}{\left(x-1\right)^2}

f'(x)=\cfrac{x^2-2x}{\left(x-1\right)^2}

Y ahora igualamos la derivada a 0 y resolvemos la ecuación:

f'(x)=0

\cfrac{x^2-2x}{\left(x-1\right)^2}=0

El término \left(x-1\right)^2} está dividiendo a todo el lado izquierdo, por tanto, lo podemos pasar multiplicando a todo el lado derecho:

x^2-2x=0\cdot \left(x-1\right)^2

x^2-2x=0

Extraemos factor común para resolver la ecuación cuadrática:

x(x-2)=0

Para que la multiplicación valga 0, uno de los dos elementos de la multiplicación tiene que ser cero. Así que igualamos cada factor a 0 y obtenemos las dos soluciones de la ecuación:

\displaystyle x\cdot(x-2) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] x-2=0 \ \longrightarrow \ \bm{x= 2} \end{cases}

Una vez hemos calculado el dominio de la función y f'(x)=0, representamos en la recta todos los puntos críticos encontrados:

Y evaluamos el signo de la derivada en cada intervalo, para saber si la función crece o decrece. Para ello, cogemos un punto de dentro de cada intervalo (nunca los puntos críticos) y miramos qué signo tiene la derivada en ese punto:

f'(x)=\cfrac{x^2-2x}{\left(x-1\right)^2}

f'(-1) = \cfrac{(-1)^2-2(-1)}{\left((-1)-1\right)^2} =\cfrac{+3}{+4} = +0,75 \ \rightarrow \ \bm{+}

f'(0,5) = \cfrac{0,5^2-2\cdot0,5}{\left(0,5-1\right)^2} = \cfrac{-0,75}{+0,25} = -3 \ \rightarrow \ \bm{-}

f'(1,5) = \cfrac{1,5^2-2\cdot1,5}{\left(1,5-1\right)^2} = \cfrac{-0,75}{+0,25} = -3 \ \rightarrow \ \bm{-}

f'(3) = \cfrac{3^2-2\cdot3}{\left(3-1\right)^2} =\cfrac{+3}{+4} = +0,75 \ \rightarrow \ \bm{+}

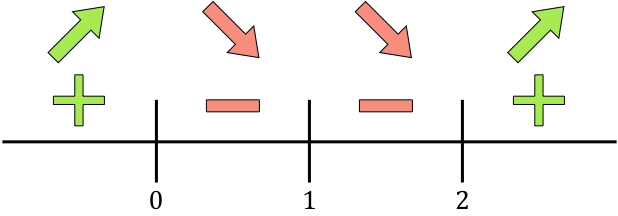
Si la derivada es positiva significa que la función crece, pero si la derivada es negativa significa que la función decrece. Por tanto, los intervalos de crecimiento y decrecimiento son:

Crecimiento: \bm{(-\infty, 0)\cup (2,+\infty)}

Decrecimiento: \bm{(0,1)\cup (1,2)}

Además, en x=0 la función pasa de ser creciente a ser decreciente, así que x=0 es un máximo relativo de la función. Y en x=2 la función pasa de ser decreciente a ser creciente, por lo que x=2 es un mínimo relativo de la función.

Y, por último, sustituimos los puntos encontrados en la función original para hallar la coordenada Y de los extremos:

f(0)=\cfrac{0^2}{0-1} = \cfrac{0}{-1} = 0 \ \longrightarrow \ (0,0)

f(2)=\cfrac{2^2}{2-1} = \cfrac{4}{1} = 4 \ \longrightarrow \ (2,4)

En definitiva, los extremos relativos de la función son:

Máximo en el punto \bm{(0,0)}

Mínimo en el punto \bm{(2,4)}

Ejercicios resueltos de máximos y mínimos de una función

Ejercicio 1

Calcula los extremos relativos de la siguiente función polinómica y determina si son máximos o mínimos:

f(x)=x^3-3x^2-9x

Los extremos relativos de la función serán aquellos puntos en los que la primera derivada de la función es igual a cero. Por lo tanto, calculamos la derivada de la función:

f(x)=x^3-3x^2-9x \ \longrightarrow \ f'(x)=3x^2-6x-9

Y ahora resolvemos la ecuación f'(x)=0:

f'(x)=0

3x^2-6x-9=0

Tenemos una ecuación de segundo grado, por tanto, aplicamos la fórmula general para resolverla:

\begin{aligned} x &=\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} =\cfrac{-(-6) \pm \sqrt{(-6)^2-4\cdot 3 \cdot (-9)}}{2\cdot 3}=\\[1.5ex]&=\cfrac{6 \pm \sqrt{144}}{6}=\cfrac{6 \pm 12}{6} =\begin{cases} \cfrac{6 + 12}{6}=\cfrac{18}{6}= 3 \\[4ex] \cfrac{6 - 12}{6}=\cfrac{-6}{6}=-1 \end{cases} \end{aligned}

Por tanto, los extremos relativos de la función son los puntos x=3 y x=-1.

Una vez sabemos los extremos relativos de la función, podemos averiguar si se tratan de un máximo o un mínimo con el signo de la segunda derivada. Así que derivamos otra vez la función:

f'(x)=3x^2-6x-9 \ \longrightarrow \ f''(x)=6x-6

Y ahora evaluamos los puntos que hemos calculado antes en la segunda derivada:

f''(3)=6(3)-6=18-6 = +12 \ \longrightarrow \ \text{M\'inimo}

f''(-1)=6(-1)-6=-6-6 = -12 \ \longrightarrow \ \text{M\'aximo}

La segunda derivada en x=3 es positiva, por lo que x=3 es un mínimo. Y la segunda derivada en x=-1 es negativa, por lo que x=-1 es un máximo.

Y, finalmente, sustituimos los puntos encontrados en la función original para hallar la coordenada Y de los extremos:

f(3)=3^3-3\cdot 3^2-9\cdot3=-27 \ \longrightarrow \ (3,-27)

f(-1)=(-1)^3-3(-1)^2-9(-1)=5 \ \longrightarrow \ (-1,5)

En definitiva, los extremos relativos de la función son:

Mínimo relativo en el punto \bm{(3,-27)}

Máximo relativo en el punto \bm{(-1,5)}

 

Ejercicio 2

Calcula los extremos relativos de la siguiente función exponencial y determina si son máximos o mínimos:

f(x)=e^x(x-1)

Primero de todo tenemos que derivar la función. Para ello, aplicamos la fórmula de la derivada de un producto:

f'(x)=e^x\cdot (x-1)+ e^x\cdot 1

f'(x)=xe^x -e^x +e^x = xe^x

Y ahora resolvemos la ecuación f'(x)=0:

f'(x)=0

xe^x=0

\displaystyle x\cdot e^x =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] e^x=0 \ \color{red}\bm{\times} \end{cases}

Un número elevado a otro nunca puede dar 0. Por lo tanto, e^x=0 no tiene solución y el único extremo relativo es x=0.

Ahora calculamos la segunda derivada de la función para saber el extremo relativo es un máximo o un mínimo:

f'(x)= xe^x \ \longrightarrow \ f''(x)= 1\cdot e^x + x \cdot e^x = e^x+xe^x

Y ahora evaluamos en la segunda derivada el extremo que hemos hallado antes, para ver si es un máximo o un mínimo:

f''(0)= e^{0}+0\cdot e^{0} = 1+0\cdot 1 = 1 \ \longrightarrow \ \text{M\'inimo}

Como la segunda derivada en x=0 es positiva, x=0 es un mínimo relativo o local.

Por último, sustituimos el punto encontrado en la función original para hallar la otra coordenada del extremo:

f(0)=e^{0}(0-1) =1\cdot (-1)=-1 \ \longrightarrow \ (0,-1)

De manera que el único extremo relativo de la función es:

Mínimo en el punto \bm{(0,-1)}

 

Ejercicio 3

Estudia la monotonía y halla los extremos relativos de la siguiente función racional:

\displaystyle f(x)=\frac{x -1 }{x^2+1}

En primer lugar, determinamos el dominio de la función. Para ello, igualamos el denominador de la fracción a cero y resolvemos la ecuación cuadrática resultante:

x^2+1 = 0

La expresión x^2+1 nunca será 0, ya que el resultado de x2 siempre será un número positivo o 0. Por tanto, al sumarle 1 nunca dará 0. Así que el dominio de la función son todos los números reales:

\text{Dom } f= \mathbb{R}

Luego estudiamos qué puntos cumplen f'(x)=0. Derivamos la función utilizando la regla del cociente:

f(x)=\cfrac{x -1 }{x^2+1} \ \longrightarrow \ f'(x)= \cfrac{1 \cdot (x^2+1) - (x-1) \cdot 2x }{\left(x^2+1}\right)^2}

f'(x)= \cfrac{x^2+1-(2x^2-2x)}{\left(x^2+1\right)^2} = \cfrac{x^2+1-2x^2+2x}{\left(x^2+1\right)^2}= \cfrac{-x^2+2x+1}{\left(x^2+1\right)^2}

Igualamos la derivada a 0 y resolvemos la ecuación:

f'(x)= 0

\cfrac{-x^2+2x+1}{\left(x^2+1\right)^2}=0

-x^2+2x+1=0\cdot \left(x^2+1\right)^2

-x^2+2x+1=0

Tenemos una ecuación de segundo grado, por lo que utilizamos la fórmula general para resolverla:

\begin{aligned}x &=\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} =\cfrac{-2 \pm \sqrt{2^2-4\cdot (-1) \cdot 1}}{2\cdot (-1)} = \\[1.5ex]&=\cfrac{-2 \pm \sqrt{8}}{-2} =\begin{cases} \cfrac{-2 + \sqrt{8}}{-2}= -0,41 \\[4ex] \cfrac{-2 - \sqrt{8}}{-2}= 2,41\end{cases} \end{aligned}

Una vez hemos calculado el dominio de la función y f'(x)=0, representamos en la recta numérica todos los puntos singulares encontrados:

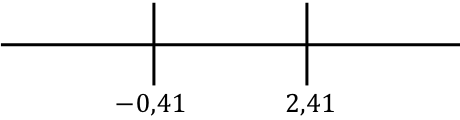
Y ahora evaluamos el signo de la derivada en cada intervalo, para saber si la función crece o decrece. De manera que cogemos un punto de dentro de cada intervalo (nunca los puntos singulares) y miramos qué signo tiene la derivada en ese punto:

f'(-1)= \cfrac{-(-1)^2+2(-1)+1}{\left((-1)^2+1\right)^2}}= \cfrac{-2}{+4} =-0,5 \ \rightarrow \ \bm{-}

f'(0)= \cfrac{-0^2+2(0)+1}{\left(0^2+1\right)^2}}= \cfrac{+1}{+1} =+1 \ \rightarrow \ \bm{+}

f'(3)= \cfrac{-3^2+2\cdot 3+1}{\left(3^2+1\right)^2}}= \cfrac{-2}{+100} =-0,02 \ \rightarrow \ \bm{-}

Si la derivada es positiva quiere decir que la función crece en ese intervalo, pero si la derivada es negativa implica que la función decrece. Por tanto, los intervalos de crecimiento y decrecimiento son:

Crecimiento: \bm{(-0,41 \ , \ 2,41)}

Decrecimiento: \bm{(-\infty \ , \ -0,41)\cup (2,41 \ , \ +\infty)}

La función pasa de ser decreciente a ser creciente en x=-0,41, así que x=-0,41 es un mínimo local de la función. Y la función pasa de ser creciente a ser decreciente en x=2,41, por lo que x=2,41 es un máximo local de la función.

Por último, sustituimos los extremos encontrados en la función original para hallar las coordenadas Y de los puntos:

f(-0,41)=\cfrac{-0,41 -1 }{(-0,41)^2+1} = \cfrac{-1,41}{1,17}= -1,21 \ \longrightarrow \ (-0,41 \ , \ -1,21)

f(2,41)=\cfrac{2,41 -1 }{2,41^2+1} = \cfrac{1,41}{6,81}= 0,21 \ \longrightarrow \ (2,41 \ , \ 0,21)

Así que los extremos relativos de la función son:

Mínimo en el punto \bm{(-0,41 \ , \ -1,21)}

Máximo en el punto \bm{ (2,41 \ , \ 0,21)}

 

Ejercicio 4

Sabemos que la función  f(x)=x^2+ax+b  pasa por el punto  (1,-2)  y tiene un extremo relativo en  x= -1 . Determina el valor de las incógnitas a  y el valor de  b .

Que la función tenga un extremo relativo en x= -1 significa que se cumple f'(-1)=0. Por tanto, calculamos la derivada de la función en x= -1 y la igualamos a 0:

f(x) = x^2+ax+b \ \longrightarrow \ f'(x)=2x+a

\left. \begin{array}{l} f'(-1)=2(-1)+a\\[2ex] f'(-1)=0\end{array} \right\} \longrightarrow 2(-1)+a=0

Y resolvemos la ecuación obtenida para hallar el valor del parámetro a:

2(-1)+a=0

-2+a=0

\bm{a=2}

De manera que la función será:

f(x)=x^2+ax+b \ \xrightarrow{a \ = \ 2} \ f(x)=x^2+2x+b

Por otro lado, nos dicen que la función pasa por el punto (1,-2) . Es decir, f(1)=-2 . Por tanto, podemos aplicar esta condición para hallar el valor de la variable b:

\left. \begin{array}{l} f(1)=1^2+2\cdot1+b \\[2ex] f(1)=-2 \end{array} \right\} \longrightarrow 1^2+2\cdot 1+b = -2

Y resolvemos la ecuación obtenida para hallar el valor del parámetro b:

1^2+2\cdot1+b=-2

1+2+b=-2

b=-2-1-2

\bm{b=-5}

Así pues, la función es:

f(x)=x^2+2x+b \ \xrightarrow{b \ = \ -5} \ f(x)=x^2+2x-5

 

6 comentarios en “Máximos y mínimos de una función (extremos relativos)”

  1. Almaada

    Hola. Excelente explicación, muchas gracias; comprendí más detalles que me facilitaron entender los conceptos que se manejan.

    Responder
    1. Funciones

      Hola Nicolás,

      Para hallar el máximo y el mínimo absoluto primero debes calcular todos los máximos y mínimos de la función. Una vez calculados todos los extremos relativos, debes mirar el valor de la función en esos puntos: el máximo absoluto es el máximo con un valor más alto y el mínimo absoluto es el mínimo con un valor más bajo.

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *