Función continua (continuidad de una función)

En este post te explicamos qué son las funciones continuas y cómo determinar si una función es continua en un punto o no. Además, encontrarás las propiedades de las funciones continuas y el análisis de la continuidad de las funciones más comunes. Finalmente, podrás practicar con ejercicios resueltos de la función continua para acabar de entender el concepto.

¿Que és una función continua?

La continuidad de una función se puede estudiar gráficamente. Una función continua es aquella función que se puede representar en una gráfica sin levantar el lápiz del papel.

Función continua

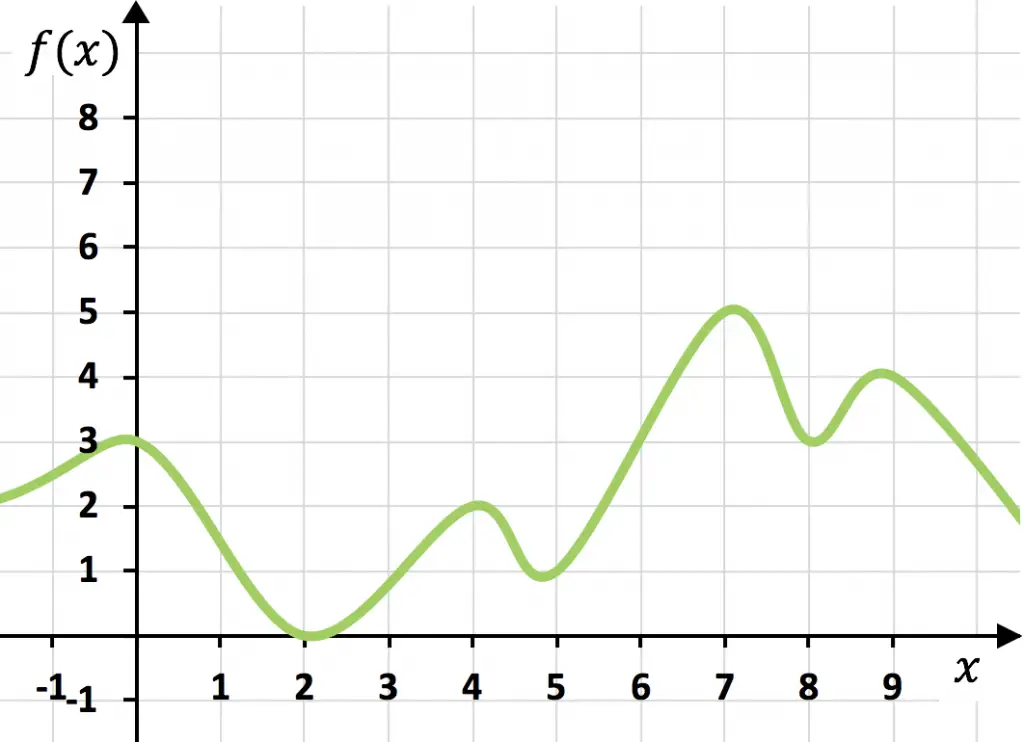
funcion continua

La función anterior es continua porque se puede dibujar en un solo trazo sin levantar la mano del papel.

Por otro lado, cuando en una función no se cumple la condición de continuidad anterior, se dice que es una función discontinua.

Función discontinua

funcion discontinua

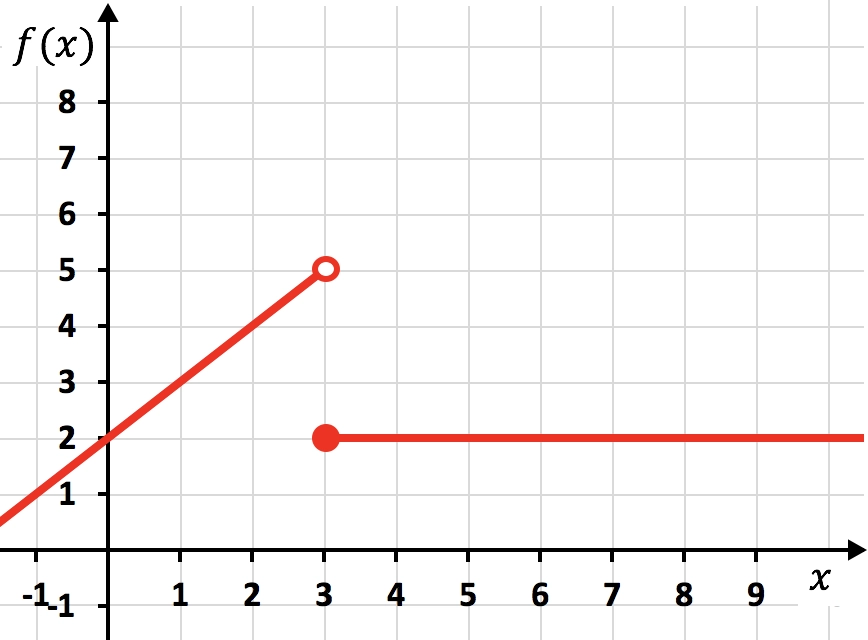
La función anterior es discontinua porque para representarla se deben hacer dos trazos con el lápiz. En este caso, la función deja de ser continua en x=3, por tanto, decimos que x=3 es un punto de discontinuidad.

Además, existen tres tipos de discontinuidades: discontinuidad evitable, discontinuidad inevitable de salto finito y discontinuidad inevitable de salto infinito. En el siguiente enlace puedes ver cómo es cada tipo de discontinuidad y qué tienen de diferente cada una de ellas:

➤ Ver: tipos de discontinuidades

Continuidad de una función en un punto

Una vez hemos visto cómo es la gráfica de una función continua, vamos a ver cómo saber si una función es continua o no analíticamente.

Matemáticamente, una función es continua en un punto si se cumplen las siguientes tres condiciones:

  1. La función existe en ese punto, es decir, existe la imagen del punto.

    2. \exists \ f(a)

  2. Existe el límite de la función en ese punto. Por tanto, los límites laterales por la izquierda y por la derecha de la función en ese punto son iguales.

    3. \displaystyle \lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) \quad \color{orange}\bm{\longrightarrow}\color{black} \quad \exists \lim_{x \to a} f(x)

  3. La imagen del punto coincide con el límite de la función en ese punto.

    4. \displaystyle f(a)=\lim_{x \to a} f(x)

De modo que si se cumplen las tres condiciones de continuidad en todos los puntos de una función, la función es continua.

A modo de ejemplo, vamos a analizar la continuidad de la siguiente función definida a trozos:

continuidad de una funcion definida a trozos

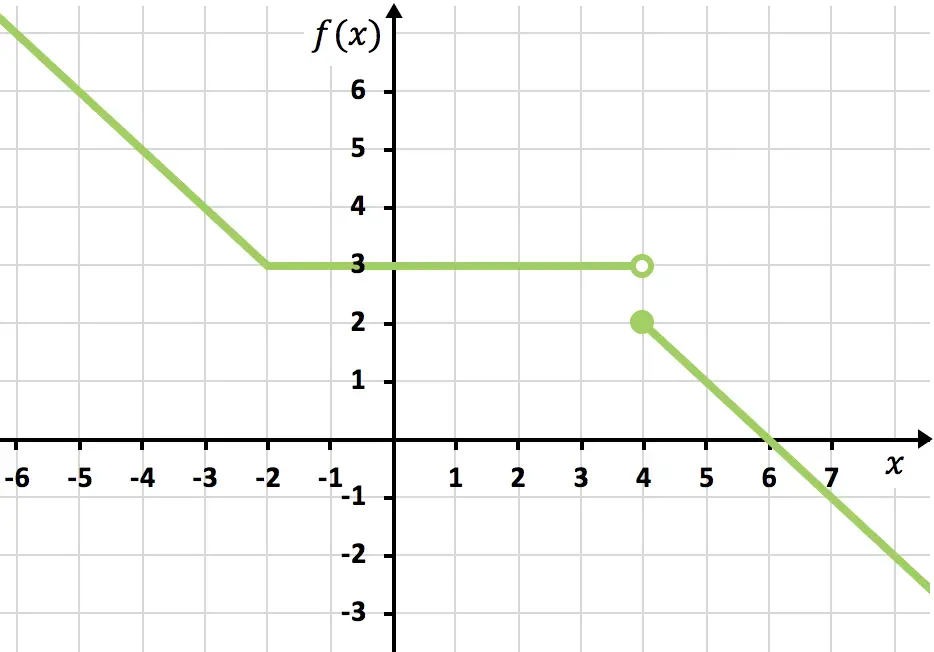
Aunque cambie de tramo, en el punto x=-2 la función es continua, ya que los límites laterales de la función en ese punto son iguales y, además, coinciden con el valor de la función en ese punto.

\lim\limits_{x \to -2^-} f(x)=\lim\limits_{x \to -2^+} f(x)= f(-2)=3

En cambio, la función no es continua en el punto x=4 porque los dos límites laterales son distintos y, por tanto, no existe el límite de la función en ese punto:

\lim\limits_{x \to 4^-} f(x)=3 \neq \lim\limits_{x \to 4^+} f(x)= 2

En definitiva, la función definida por partes es continua en todos los números reales excepto en x=4, donde tiene una discontinuidad.

También podemos comprobar que la función es discontinua en x=4 porque al representarla gráficamente es necesario levantar el lápiz del papel en este punto.

Continuidad de funciones elementales

Algunos tipos de funciones son continuas debido a sus características:

  • Las funciones constantes son continuas en todos los reales.

f(x)=k

  • Las funciones polinómicas son continuas en todos los números reales.

f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n

  • Las funciones racionales (o fraccionarias) son continuas en todos los números reales excepto en aquellos valores que anulan el denominador de la fracción, en esos puntos la función presenta una discontinuidad.

f(x)=\cfrac{p(x)}{q(x)}

  • Las funciones exponenciales son continuas en todo el conjunto de números reales:

f(x)=a^x

  • Las funciones logarítmicas son continuas en todos aquellos puntos que hacen que su argumento sea positivo.

f(x)=\log_a (x)

  • La continuidad de las funciones irracionales, o funciones con raíces, depende del índice del radical (n). Si el índice es par, son funciones continuas en todos los puntos que hacen igual o mayor que cero el argumento de la raíz. Pero si el índice es impar, son funciones continuas en todos los números reales.

f(x)=\sqrt[n]{x}

  • La continuidad de las funciones trigonométricas depende del tipo de función. La función seno y la función coseno son continuas en todo el conjunto de números reales, pero la función tangente es discontinua en los puntos \displaystyle x=\frac{\pi}{2}+k\pi (donde k es un número entero).

f(x)=sen(x)\qquad f(x)=cos(x)\qquad f(x)=tg(x)

Propiedades de las funciones continuas

Sean f(x) y g(x) dos funciones continuas en el punto x=a, entonces:

  • La suma de dos funciones continuas en un punto es otra función continua en ese punto.

f(x)+g(x)

  • El producto de dos funciones continuas en punto es igual a otra función continua en ese punto.

f(x)\cdot g(x)

  • La división de dos funciones continuas en un punto da como resultado otra función continua en ese punto, siempre y cuando ese punto no anule la función divisora.

\cfrac{f(x)}{g(x)}\qquad g(a)\neq 0

  • La composición de dos funciones continuas en un punto da lugar a una función continua en ese mismo punto.

f(x)\circ g(x)

➤ Ver: ¿qué es una función compuesta?

Ejercicios resueltos de la continuidad de una función

Ejercicio 1

Encuentra las discontinuidades de la función representada en el siguiente gráfico. Determina también qué tipo de discontinuidad son.

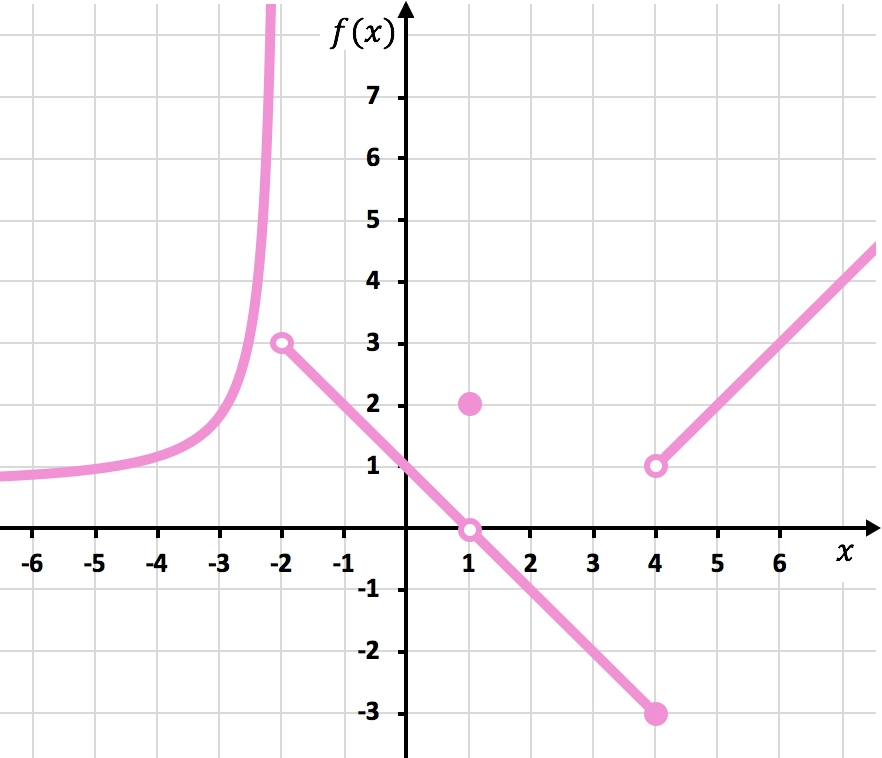
ejercicio resuelto discontinuidades de funciones

Nota: para hacer este ejercicio te recomendamos que primero veas cuáles son los diferentes tipos de discontinuidades y cómo se identifican. Puedes ver la explicación en el enlace del principio de tipos de discontinuidades.

Para dibujar la función hay que levantar el lápiz en x=-2, en x=1 y en x=4. Por tanto, la función es discontinua en estos tres puntos.

En x=-2 el límite lateral por la izquierda es +∞, y el límite lateral por la derecha es 3. Así pues, como uno de los límites laterales es infinito, la función tiene una discontinuidad inevitable de salto infinito en x=-2.

\displaystyle \lim_{x \to -2^-} f(x) = +\infty \ \neq \ \lim_{x \to -2^+} f(x) = 3

El límite de la función en x=1 es 0 y, en cambio, el valor de la función en x=1 es igual a 2. Por tanto, la función tiene una discontinuidad evitable en x=1.

\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 0 \ \bm{\longrightarrow} \ \lim_{x \to 1} f(x) = 0

\displaystyle \lim_{x \to 1} f(x) = 0 \neq f(0) = 2

En x=4 el límite lateral por la izquierda es -3, y el límite lateral por la derecha es 1. Por tanto, como los dos límites laterales son diferentes y ninguno de ellos da infinito, la función tiene una discontinuidad inevitable de salto finito en x=4.

\displaystyle \lim_{x \to 4^-} f(x) = -3 \ \neq \ \lim_{x \to 4^+} f(x) = 1

 

Ejercicio 2

Determina los puntos en los que la función representada en la siguiente gráfica es discontinua.

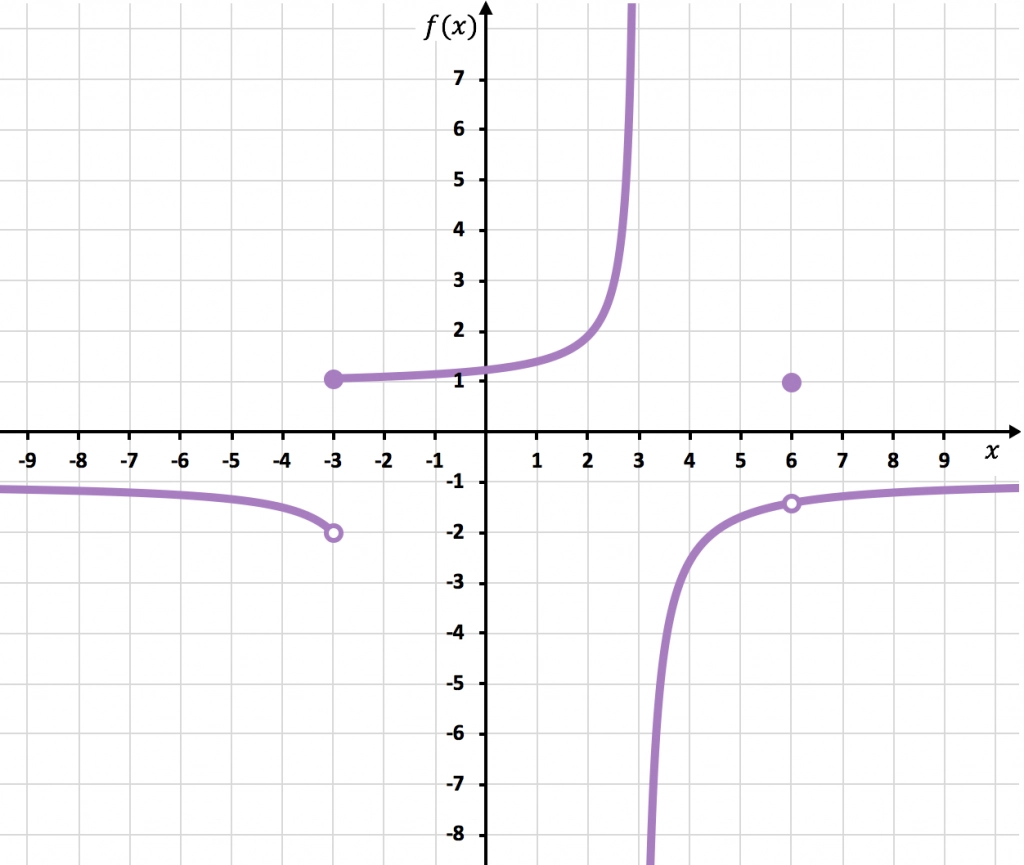
ejercicio resuelto de tipos de discontinuidades de una funcion

En el punto x=6 la función se interrumpe, ya que hay un punto abierto. El límite cuando x tiende a 6 es -1,4 pero f(6)=1. De manera que la función tiene una discontinuidad evitable en x=6 porque el valor del límite no coincide con el valor de la función:

\displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4

\displaystyle\lim_{x \to 6} f(x)=-1,4 \neq f(6)=1

En x=-3 los límites laterales no coinciden y ninguno da infinito. Así que la función tiene una discontinuidad inevitable de salto finito en x=-3.

\displaystyle \lim_{x \to -3^-} f(x)=-2 \neq \lim_{x \to -3^+} f(x)=1

Y, por último, la función tiene una discontinuidad inevitable de salto infinito en x=3, ya que al menos un límite lateral en ese punto da como resultado infinito.

\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty

 

Ejercicio 3

Analiza la continuidad de la siguiente función racional:

\displaystyle f(x)= \frac{2}{x-5}

Las funciones racionales son continuas en todo su dominio, es decir, en todos los números reales excepto en los valores que anulan el denominador. Por lo tanto, igualamos el denominador de la función racional a cero para ver qué puntos no pertenecen al dominio:

x-5=0

x=5

\text{Dom } f = \mathbb{R} - \{5\}

De manera que la función será continua en todos los puntos menos en x=5.

 

Ejercicio 4

Analiza la continuidad de la siguiente función definida a trozos:

\displaystyle f(x)= \left\{ \begin{array}{lcl} 5x-2 & \text{si} & x < 1 \\[2ex] x^2+2 & \text{si} & x \geq 1 \end{array} \right.

La función es continua tanto en el primer tramo, 5x-2 , como en el segundo tramo, x^2+2, ya que son funciones polinómicas.

De forma que el único punto en el que la función podría ser discontinua es el punto de ruptura de la función a trozos. Así que vamos a calcular los límites laterales en ese punto:

\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1} (5x-2)=5\cdot 1-2=\bm{3}

\displaystyle \lim_{x \to 1^+} f(x) = \lim_{x \to 1} (x^2+2)=1^2+2=\bm{3}

Los dos límites laterales coinciden, por lo tanto, el límite de la función cuando x tiende a 1 es igual a 3:

\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 3 \ \bm{\longrightarrow} \ \exists \lim_{x \to 1} f(x) = 3

Además, la imagen de x=1 también es 3:

f(1)=1^2+2=\bm{3}

Así pues, como el límite de la función en x=1 es igual a la imagen de dicho punto, la función es continua en el punto x=1. Y, en consecuencia, es continua en todos los números reales.

\displaystyle f(1)=\lim_{x \to 1} f(x)

 

Ejercicio 5

Estudia la continuidad de la siguiente función irracional:

f(x)=\sqrt{2x+6}

Es un función radical de índice par, por tanto, la función será continua siempre que el argumento del radical sea más grande que 0 (porque no existe la raíz cuadrada de un número negativo):

2x+6\ge 0

Resolvemos la inecuación:

2x\ge -6

x\ge \cfrac{-6}{2}

x\ge -3

La solución son todos los números más grandes o iguales que -3. Así que la función es continua en el intervalo de su dominio:

\mathbf{Dom } \ \bm{f = [-3,+\infty) }

 

Ejercicio 6

Analiza la continuidad de la siguiente función logarítmica:

f(x)=\log_3 (-3x+6)

Se trata de una función logarítmica, y no existe ni el logaritmo de un número negativo ni el logaritmo de 0. Por tanto, la función existirá siempre que el argumento del logaritmo sea positivo (más grande que cero):

-3x+6>0

Resolvemos la inecuación:

-3x>-6

x<\cfrac{-6}{-3}

Recuerda que al pasar dividiendo un número negativo al otro lado de una inecuación debes girar el signo de la desigualdad.

x<2

La solución son todos los números más pequeños que 2. Así que el dominio de la función es:

\mathbf{Dom } \ \bm{f = (-\infty,2) }

De manera que la función es continua en todos los puntos de su dominio.

 

Ejercicio 7

Calcula la continuidad de la siguiente función:

f(x)=\cfrac{4x-2}{\sqrt{-2x-8}}

En el denominador de la fracción tenemos un radical de índice par, por tanto, la función existirá siempre que el contenido de la raíz sea igual o mayor que cero:

-2x-8\geq 0

Pero, además, la raíz está en el denominador de la fracción, y el denominador de una fracción nunca puede ser 0. De modo que la función solo existirá si el contenido de la raíz es estrictamente más grande que 0:

-2x-8> 0

Ahora resolvemos la inecuación:

-2x>8

x<\cfrac{8}{-2}

Recuerda que cuando en una inecuación cambiamos de lado un número negativo multiplicando o dividiendo también tenemos que girar el signo de la inecuación.

x<-4

El resultado son todos los números más pequeños que -4. Así que el dominio de la función, y por tanto su continuidad, quedan definidos por el siguiente intervalo:

\mathbf{Dom } \ \bm{f = (-\infty,-4) }

 

Ejercicio 8

Calcula el valor de k para que la función sea continua en todo \mathbb{R} .

\displaystyle f(x)= \left\{ \begin{array}{lcl} kx-1 & \text{si} & x \leq 2 \\[2ex] 3x^2 - 5 & \text{si} & x > 2 \end{array} \right.

Para que la función sea continua, los dos límites laterales en el punto de ruptura deben dar el mismo resultado. Así que primero calculamos el límite lateral en el punto de ruptura del trozo que no tiene k:

\displaystyle \lim_{x \to 2^+} f(x) = \lim_{x \to 2} (3x^2 - 5) = 3\cdot 2^2-5=\bm{7}

Por tanto, para que la función definida a trozos sea continua, el otro límite lateral también tiene que dar 7.

Intentamos calcular el otro límite lateral:

\displaystyle \lim_{x \to 2^-} f(x) = \lim_{x \to 2} (kx-1) = k\cdot2 -1= 2k-1

Entonces, para que la función sea continua, los dos límites laterales de cualquier punto deben dar el mismo resultado. Por lo que igualamos la expresión obtenida del límite a 7 (el resultado del otro límite lateral).

2k -1= 7

Y, por último, resolvemos la ecuación resultante para hallar el valor de k:

2k-1 = 7

2k = 7 +1

2k = 8

k = \cfrac{8}{2}

\bm{k =4}

 

10 comentarios en “Función continua (continuidad de una función)”

  3. Gerardo

    Buenísimo, sólo un detalle, cuando en el ejercicio 6 de la continuidad de la función logaritmica, cuando haces la inecuación a ambos lados negativa, al multiplicar por -1, ¿no has de cambiar el signo de la desigualdad?. porque si el resultado como te da x>2, el paréntesis (-3x+6) te saldrá negativo por lo que debiera ser x<2.. Yo creo, pero te felicito porque he visto pocos temas complejos,como éste, tan bien explicados, por no decir ninguno

    Responder
    1. Funciones

      Hola Gerardo,

      Tienes toda la razón, ya se ha corregido. ¡Gracias por informar de este pequeño fallo!

      ¡Y muchas gracias por la felicitación! ❤

  4. Martín

    Gracias por compartir! Estoy cursando Cálculo diferencial e integral en una variable y me ha ayudado mucho jeje

    Responder
  5. Nicolás

    Fascinado con tu página, es lo más épico que haya podido encontrar, se las recomiendo a todos los que me preguntan cosas y no recuerdo bien como explicárselas, siga así socio. Por cierto una recomendación, sería rentable agregar la continuidad de funciones de valor absoluto, aunque parezca un poco obvio, suele preguntarse mucho por los profesores el tema con valores absolutos, no solo en continuidad, también en otras áreas. Por ejemplo, ya me preguntaron si la función f : R –> R ; f(x) = |x| es continua en x=0, es una pregunta de Ver. y Fal. justificando en ambos casos. Algunos aceptan justificar con un gráfico, otros no, y exigen analíticamente. Eso, gracias por tanto esfuerzo en simplificar las matemáticas.

    Responder
    1. Funciones

      ¡Muchas gracias de nuevo Nicolás! ¡Me alegra de que te guste tanto nuestra página web!

      Sí que tenemos un artículo en el que explicamos las funciones con valor absoluto y cómo analizar su continuidad. Puedes encontrar el artículo buscando «valor absoluto» en el buscador de nuestra página.

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *