▷ ¿Cuáles son todos los tipos de discontinuidades?

Aquí encontrarás qué tipos de discontinuidades existen. Además, podrás ver ejemplos de todos los tipos de discontinuidades y podrás practicar con ejercicios resueltos de los tipos de discontinuidades de las funciones.

Índice

¿Cuáles son todos los tipos de discontinuidades?

Existen tres tipos de discontinuidades, que son:

Discontinuidad evitable: los límites laterales de una función en un punto no coinciden con el valor de la función.
Discontinuidad inevitable de salto finito: los límites laterales de una función en un punto son diferentes.
Discontinuidad inevitable de salto infinito: uno de los límites laterales de la función da infinito o no existe.

Para acabar de entender los conceptos, vamos a explicar más detalladamente cada tipo de discontinuidad y vamos a ver ejemplos de funciones con los tres tipos de discontinuidades.

Discontinuidad evitable

La discontinuidad evitable es un tipo de discontinuidad que tiene una función en un punto si existe el límite en ese punto pero este no coincide con el valor de la función o la imagen de la función no existe.

$\displaystyle \exists \lim_{x \to a} f(x) \neq f(a) \qquad | \qquad \displaystyle \exists\lim_{x \to a} f(x) \text{ y } \ \cancel{\exists} \ f(a)$

Los límites laterales de esta función son iguales entre sí, pero son distintos al valor de la función en ese punto. Por lo tanto, la función presenta una discontinuidad evitable.

$\displaystyle \left. \begin{array}{l}\displaystyle \lim_{x \to a^-} f(x) =b \\[3ex] \displaystyle \lim_{x \to a^+} f(x)=b \end{array} \right\} \ \bm{\longrightarrow} \ \lim_{x \to a} f(x)=b$

$\displaystyle \lim_{x \to a} f(x)=b \qquad f(a)=c$

$\displaystyle \exists \lim_{x \to a} f(x) \neq f(a)$

discontinuidad evitable de una funcion sin imagen

La función del ejemplo anterior tiene una discontinuidad evitable por que los límites laterales en x=a valen lo mismo, pero la imagen de la función en ese punto no existe.

$\displaystyle \left. \begin{array}{l}\displaystyle \lim_{x \to a^-} f(x) =b \\[3ex] \displaystyle \lim_{x \to a^+} f(x)=b \end{array} \right\} \ \bm{\longrightarrow} \ \lim_{x \to a} f(x)=b$

$\displaystyle \lim_{x \to a} f(x)=b \qquad \cancel{\exists} \ f(a)$

➤ Ver: límites laterales de una función

Discontinuidad inevitable de salto finito

La discontinuidad inevitable de salto finito es un tipo de discontinuidad que presenta una función en un punto cuando los límites laterales de la función en ese punto no son iguales.

$\displaystyle \lim_{x \to a^-} f(x) \neq \lim_{x \to a^+} f(x)$

Por ejemplo, los límites laterales de la siguiente función definida a trozos en el punto de cambio de definición son distintos, en consecuencia, la función tiene una discontinuidad inevitable de salto finito en ese punto.

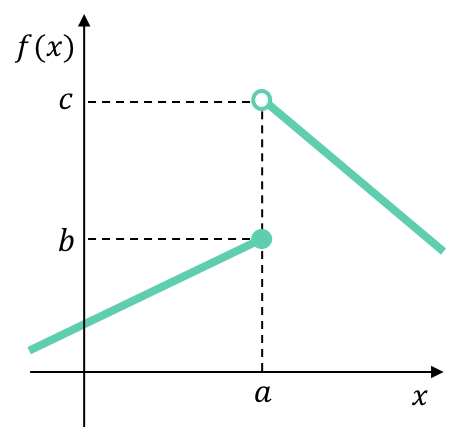
discontinuidad inevitable de salto finito

$\displaystyle \lim_{x \to a^-} f(x)=b \qquad \lim_{x \to a^+} f(x)=c$

$\displaystyle \lim_{x \to a^-} f(x) \neq \lim_{x \to a^+} f(x)$

Este tipo de discontinuidad suele aparecer en funciones definidas a trozos (o por partes).

➤ Ver: continuidad de una función definida a trozos

Discontinuidad inevitable de salto infinito

La discontinuidad inevitable de salto infinito es un tipo de discontinuidad que tiene una función en en punto si alguno de los límites laterales en ese punto es infinito o no existe.

$\displaystyle \lim_{x \to a^-} f(x) = \pm \infty \qquad \lim_{x \to a^+} f(x)= \pm \infty$

El límite lateral por la izquierda de la siguiente función da un número real, pero el límite lateral por la derecha da infinito. De modo que la función presenta una discontinuidad inevitable de salto infinito.

$\displaystyle \lim_{x \to a^-} f(x)=b \qquad \lim_{x \to a^+} f(x)=+\infty$

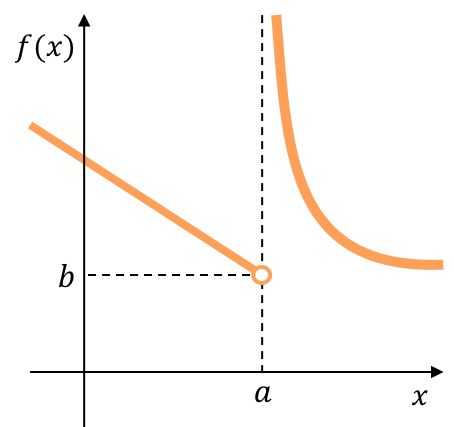
A continuación, puedes ver una función representada gráficamente cuyos dos límites laterales dan infinito y, por tanto, la función tiene una discontinuidad inevitable de salto infinito.

$\displaystyle \lim_{x \to a^-} f(x)=-\infty \qquad \lim_{x \to a^+} f(x)=+\infty$

Este tipo de discontinuidad suele producirse en funciones racionales (o fraccionarias).

Ejercicios resueltos de tipos de discontinuidades

Ejercicio 1

Determina qué tipo de discontinuidad tiene la siguiente función definida a trozos en el punto x=3:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} -2x+1 & \text{si} & x\leq 3 \\[2ex] 4x - 5 & \text{si} & x > 3 \end{array} \right.$

Ver solución

Tanto el dominio del primer trozo de la función, $-2x+1$ , como el del segundo trozo, $4x-5$ , son todos los números reales porque son funciones polinómicas.

Así que el único punto en el que la función podría ser discontinua es el punto de ruptura de la función a trozos. Por lo que vamos a calcular los límites laterales en ese punto:

$\displaystyle \lim_{x \to 3^-} f(x)=\lim_{x \to 3} (-2x+1) = -2\cdot 3+1=-5$

$\displaystyle \lim_{x \to 3^+} f(x)=\lim_{x \to 3}(4x-5)=4\cdot 3-5=7$

$\displaystyle \lim_{x \to 3^-} f(x) \neq \lim_{x \to 3^+} f(x)$

Los dos límites laterales en x=3 dan diferente. Por tanto, el punto x=3 es una discontinuidad inevitable de salto finito.

Ejercicio 2

Halla qué tipo de discontinuidad presenta la siguiente función racional en los puntos que no pertenecen a su dominio:

$f(x)= \cfrac{x^2-4}{x+2}$

Ver solución

Lógicamente, para resolver este ejercicio primero tenemos que hallar el dominio de la función. Así que, como es una función racional, igualamos el denominador a 0 y solucionamos la ecuación resultante:

$x+2=0$

$x=-2$

$\text{Dom } f = \mathbb{R} - \{-2\}$

De manera que la función será continua en todos los puntos menos en x=-2, por lo que vamos a ver qué tipo de discontinuidad es el punto x=-2. Para ello, calculamos el límite de la función en el punto:

$\displaystyle \lim_{x \to -2} \cfrac{x^2-4}{x+2} = \cfrac{ (-2)^2-4}{-2+2}= \cfrac{0}{0}$

Pero obtenemos la indeterminación cero entre cero, por tanto, factorizamos los polinomios del numerador y del denominador y simplificamos:

$\displaystyle \lim_{x \to -2} \cfrac{x^2-4}{x+2}=\lim_{x \to -2} \cfrac{ (x-2)\cancel{(x+2)}}{\cancel{x+2}} =\lim_{x \to -2} (x-2)$

Ahora resolvemos el límite:

$\displaystyle \lim_{x \to -2} (x-2) =-2-2=-4$

Por tanto, el límite de la función en el punto x=-2 sí que existe y da -4. Vamos a comprobar ahora si existe $f(-2):$

$f(-2)=\cfrac{(-2)^2-4}{-2+2}= \cfrac{4-4}{0} = \cfrac{0}{0} \quad \bm{\longrightarrow} \quad \cancel{\exists} \ f(2)$

En el cálculo de la imagen de una función, la indeterminación 0/0 no se puede simplificar y no tiene solución. Así que $f(-2)$ no existe.

En conclusión, el límite de la función en x=-2 existe, pero $f(-2)$ no. Por tanto, x=-2 es una discontinuidad evitable.

Ejercicio 3

Analiza la continuidad de la siguiente función racional:

$\displaystyle f(x)= \frac{2}{x-5}$

Ver solución

Para ver si es una función continua, primero debemos calcular su dominio. Así que igualamos el denominador de la función racional a cero para ver qué puntos no pertenecen al dominio:

$x-5=0$

$x=5$

$\text{Dom } f = \mathbb{R} - \{5\}$

De manera que la función será continua en todos los puntos menos en x=5. Por tanto, vamos a ver qué tipo de discontinuidad es x=5 calculando el límite en ese punto:

$\displaystyle \lim_{x \to 5} \frac{2}{x-5} = \frac{2}{5-5} = \frac{2}{0} = \infty$

Nos encontramos con la indeterminación de un número dividido entre 0. Así que calculamos los límites laterales de la función en x=5:

$\displaystyle \lim_{x \to 5^{-}} \frac{2}{x-5}=\frac{2}{4,999-5}=\frac{2}{-0}= \bm{-\infty}$

$\displaystyle \lim_{x \to 5^{+}} \frac{2}{x-5}=\frac{2}{5,001-5}=\frac{2}{+0}=\bm{+\infty}$

El límite lateral por la izquierda de la función en x=5 da menos infinito y el límite lateral por la derecha da más infinito. Por lo tanto, la función tiene una discontinuidad inevitable de salto infinito en x=5, ya que como mínimo un límite lateral en ese punto tiende al infinito.

Ejercicio 4

Determina todas las discontinuidades de la función a trozos representada en la siguiente gráfica:

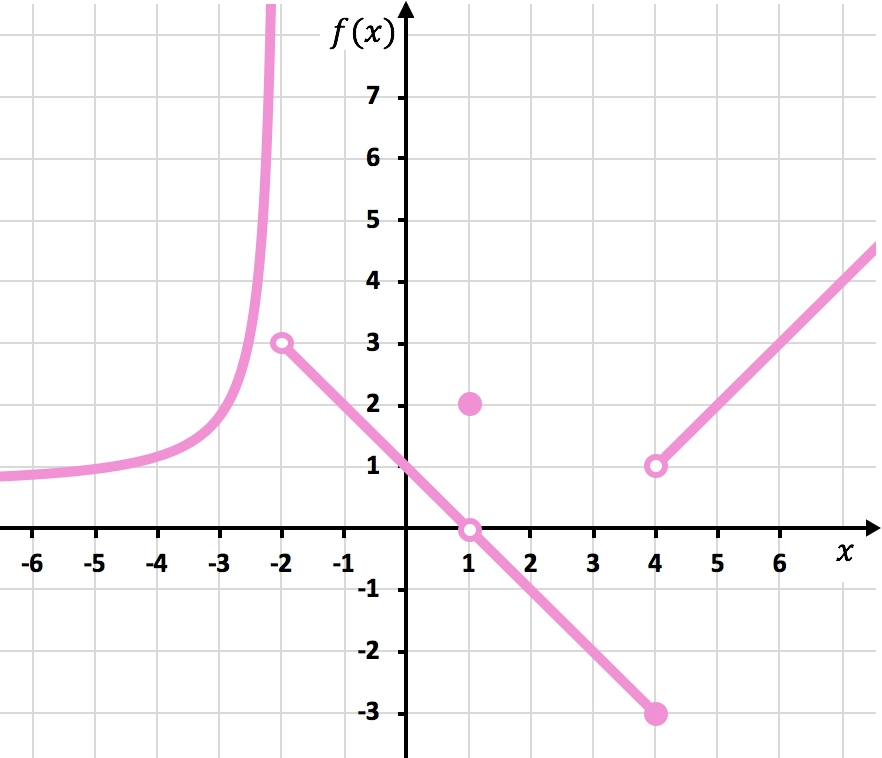
ejercicio resuelto discontinuidades de funciones

Ver solución

Para dibujar la función hay que levantar el lápiz en x=-2, en x=1 y en x=4. Por tanto, la función es discontinua en estos tres puntos.

En x=-2 el límite lateral por la izquierda es +∞, y el límite lateral por la derecha es 3. Así pues, como uno de los límites laterales es infinito, la función tiene una discontinuidad inevitable de salto infinito en x=-2.

$\displaystyle \lim_{x \to -2^-} f(x) = +\infty \ \neq \ \lim_{x \to -2^+} f(x) = 3$

El límite de la función en x=1 es 0 y, en cambio, el valor de la función en x=1 es igual a 2. Por tanto, la función tiene una discontinuidad evitable en x=1.

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 0 \ \bm{\longrightarrow} \ \lim_{x \to 1} f(x) = 0$

$\displaystyle \lim_{x \to 1} f(x) = 0 \neq f(1) = 2$

En x=4 el límite lateral por la izquierda es -3, y el límite lateral por la derecha es 1. Por tanto, como los dos límites laterales son diferentes y ninguno de ellos da infinito, la función tiene una discontinuidad inevitable de salto finito en x=4.

$\displaystyle \lim_{x \to 4^-} f(x) = -3 \ \neq \ \lim_{x \to 4^+} f(x) = 1$

Ejercicio 5

Halla todas las asíntotas y discontinuidades de la función representada en el siguiente gráfico:

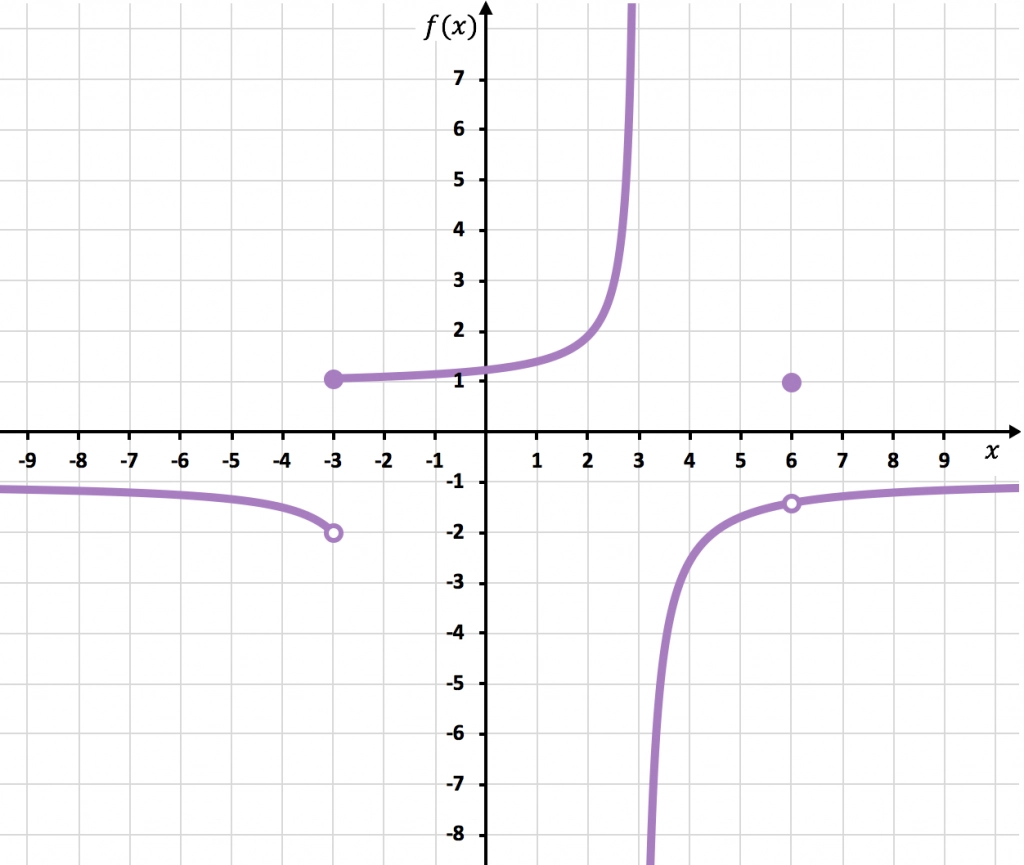
ejercicio resuelto de tipos de discontinuidades de una funcion

Ver solución

Asíntotas

La función se acerca mucho a la recta vertical x=3 pero nunca llega a tocarla. Además, el límite lateral por la izquierda en x=3 es +∞ y el límite lateral por la derecha es -∞. Por tanto, x=3 es una asíntota vertical.

$\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty$

Y lo mismo sucede con la recta horizontal y=-1, la función se aproxima mucho a y=-1 pero nunca llega a cruzarla. Además, el límite de la función cuando x tiende a +∞ y -∞ es -1. Por tanto, y=-1 es una asíntota horizontal.

$\displaystyle \lim_{x \to +\infty} f(x)=-1 \qquad \lim_{x \to -\infty} f(x)=-1$

Discontinuidades

En x=6 la función se interrumpe, ya que hay un punto abierto. El límite cuando x tiende a 6 es -1,4 pero f(6)=1. De manera que la función tiene una discontinuidad evitable en x=6 porque el valor del límite no coincide con el valor de la función:

$\displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4$

$\displaystyle\lim_{x \to 6} f(x)=-1,4 \neq f(6)=1$

En x=-3 los límites laterales no coinciden y ninguno da infinito. Así que la función tiene una discontinuidad inevitable de salto finito en x=-3.

$\displaystyle \lim_{x \to -3^-} f(x)=-2 \neq \lim_{x \to -3^+} f(x)=1$

Y, por último, la función tiene una discontinuidad inevitable de salto infinito en x=3, ya que al menos un límite lateral en ese punto da como resultado infinito.

$\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty$

10 comentarios en “Tipos de discontinuidades”

Carlos Nores
14/11/2021 a las 15:36

Excelente informe…impecable explicación

Responder
1. Funciones
  17/11/2021 a las 14:39
  
  ¡Muchas gracias Carlos!
Esther
15/11/2021 a las 09:11

muchas gracias por lo que hacen, me aclararon varias dudas, los ejemplos son claros de igual manera la explicación felicidades

Responder
1. Funciones
  17/11/2021 a las 14:39
  
  ¡Muchas gracias Esther! Siempre intentamos hacerlo lo mejor posible. 🙂
Khashayar
31/12/2021 a las 15:15

Fenomenal.

Responder
1. Funciones
  04/01/2022 a las 13:36
  
  ¡Gracias Khashayar!
Romina Moncada
25/07/2022 a las 22:24

Hermoso material muchísimas gracias!!!

Responder
1. Funciones
  28/07/2022 a las 13:06
  
  ¡Gracias a ti Romina por comentar! 🙂
María
22/04/2023 a las 19:00

¡Gracias por esto! No lo entendía hasta que vi esta página.
Y los ejercicios con soluciones… ¡maravillosos!
¡Gracias, Gracias, Gracias!

Responder
1. Funciones
  24/04/2023 a las 11:58
  
  ¡Muchas gracias por todo el cariño María! ❤