Límites laterales

En este post te explicamos qué es el límite lateral de una función (con ejemplos). También te enseñamos cómo calcular límites laterales de una función por la izquierda y por la derecha, tanto gráficamente como numéricamente. Además, podrás practicar con ejercicios resueltos paso a paso de límites laterales.

¿Qué son los límites laterales?

Los límites laterales de una función en un punto estudian el comportamiento de la función alrededor de dicho punto. Existe el límite lateral por la izquierda y el límite lateral por la derecha, que analizan el valor de la función respectivamente a la izquierda y a la derecha del punto en cuestión.

Límites laterales por la izquierda y por la derecha

Como hemos visto en la definición de límites laterales, hay dos tipos: los límites laterales por la izquierda y los límites laterales por la derecha.

El límite lateral de la función por la izquierda se expresa con un signo menos en el punto donde se analiza el límite y, por otro lado, el límite lateral por la derecha se indica con el signo más.

Fíjate en el siguiente ejemplo para entender mejor el significado de los límites laterales:

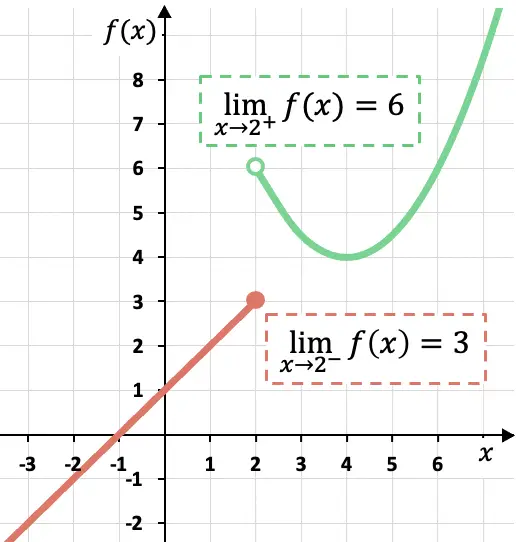
Como puedes ver en la representación gráfica de esta función definida a trozos, los límites laterales dependen del lado en el que se calculen.

En este caso, la función tiende a 3 cuando x tiende a 2 por la izquierda, ya que la función toma valores cada vez más próximos a 3 cuando x se aproxima a x=2 por su izquierda.

En cambio, el límite lateral de la función en x=2 por la derecha vale 6. Porque si nos acercamos al punto x=2 desde su derecha, la función va tomando valores cada vez más cercanos a f(x)=6.

Por otra parte, debes saber que los límites laterales poseen las mismas propiedades que los límites ordinarios. En el siguiente enlace puedes ver cuáles son las propiedades de los límites:

➤ Ver: propiedades de los límites

Límites laterales iguales

Acabamos de ver un ejemplo en el que los límites laterales de una función son distintos, pero… ¿qué pasa si los límites laterales son iguales?

Si los dos límites laterales de una función en un punto existen y son iguales, existe el límite de la función en dicho punto y el resultado del límite es el valor de los límites laterales.

Es decir, para que exista el límite de una función en un punto, se debe cumplir la siguiente condición:

Por lo tanto, si los límites laterales de una función en un punto son diferentes, el límite de la función en ese punto no existe.

Además, que el límite de una función en un punto exista es una condición imprescindible para que sea una función continua en un punto.

Vamos a resolver un ejemplo para acabar de comprender el concepto de límites laterales:

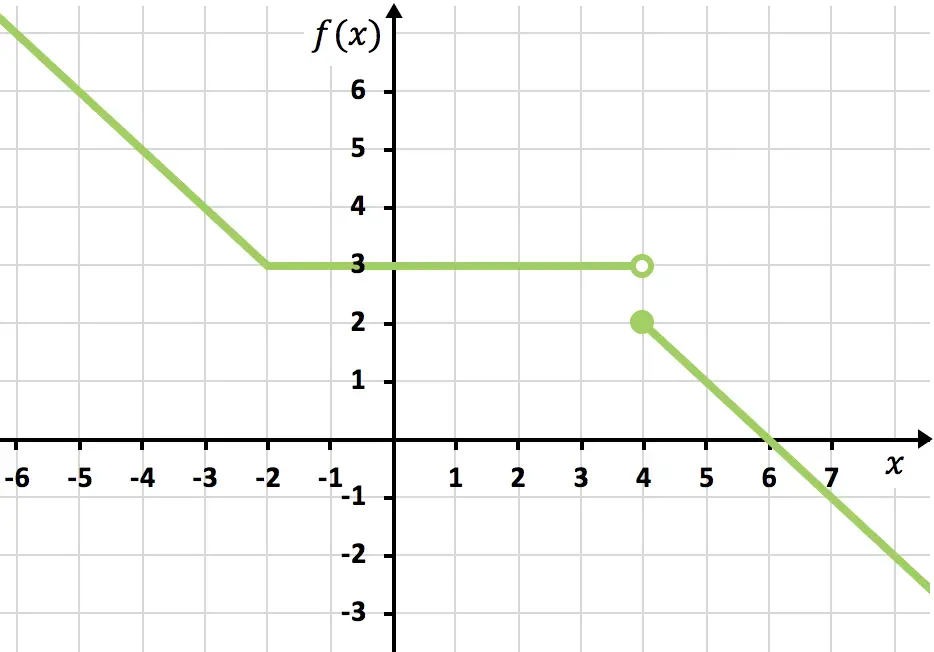
Los límites laterales en el punto x=-2 de la función representada gráficamente coinciden, ya que el valor de la función tiende a 3 indistintamente de si nos aceramos a x=-2 por la izquierda o por la derecha. En consecuencia, el límite de la función en x=-2 es igual a 3.

En cambio, en el punto x=4 los límites laterales son distintos, ya que por la izquierda la función se aproxima a f(x)=3 pero por la derecha la función se aproxima a f(x)=2. De modo que el límite de la función en este punto no existe.

Cálculo de límites laterales

Vista la definición de los límites laterales, vamos a ver cómo se calculan numéricamente resolviendo el siguiente ejemplo:

Si calculamos el límite como siempre, obtenemos la indeterminación de un número real dividido entre 0:

Sin embargo, al hacer el cálculo de los límites laterales no obtenemos ninguna indeterminación.

Para calcular el límite lateral de la función por la izquierda en x=2, tenemos que coger un número menor que x=2 pero que sea muy próximo a él, por ejemplo x=1,999.

En este caso, el denominador será un número negativo de valor muy pequeño pero que no llega a ser cero, y suele representarse con un cero y el signo menos delante:

Por lo tanto, el resultado del límite lateral es menos infinito, porque cualquier número dividido entre 0 da infinito y positivo entre negativo da negativo:

Podemos comprobar que la función tiende a menos infinito calculando imágenes de la función con valores cada vez más cercanos a x=2 por la izquierda.

Asimismo, para hallar el límite de la función en el punto x=2 por la derecha podemos aplicar el mismo razonamiento: cogemos un valor mayor que 2 pero muy cercano a él, como por ejemplo 2,001.

Del mismo modo, se puede verificar que la función tiende a más infinito calculando imágenes de la función con valores cada vez más cercanos a x=2 por la derecha.

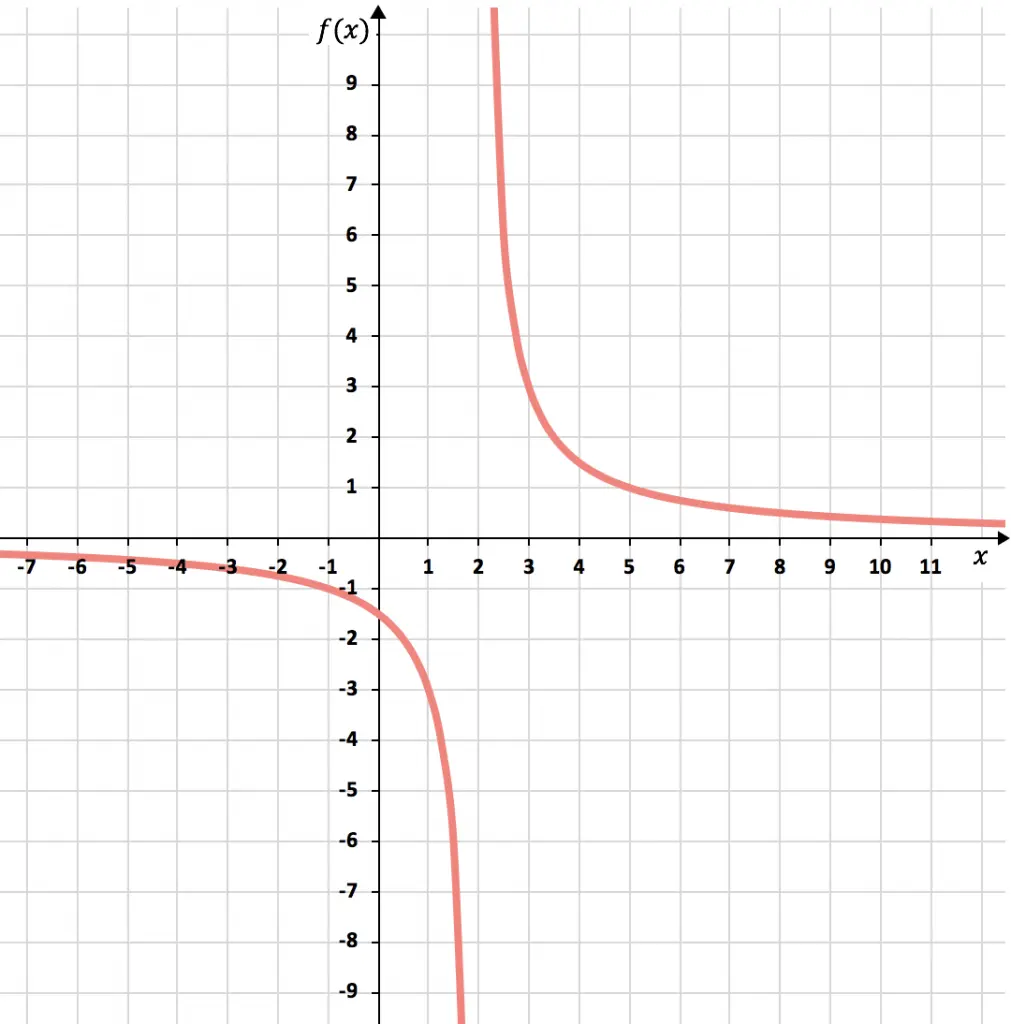
En el siguiente gráfico puedes ver representada la función analizada. Como puedes apreciar, el límite lateral de la función en el punto x=2 por la izquierda es menos infinito, y el límite lateral de la función en el punto x=2 por la derecha es más infinito.

Ejercicios resueltos de límites laterales

Ejercicio 1

Halla los límites laterales de la siguiente función definida a trozos en los puntos donde cambia la definición (x=-2 y x=4).

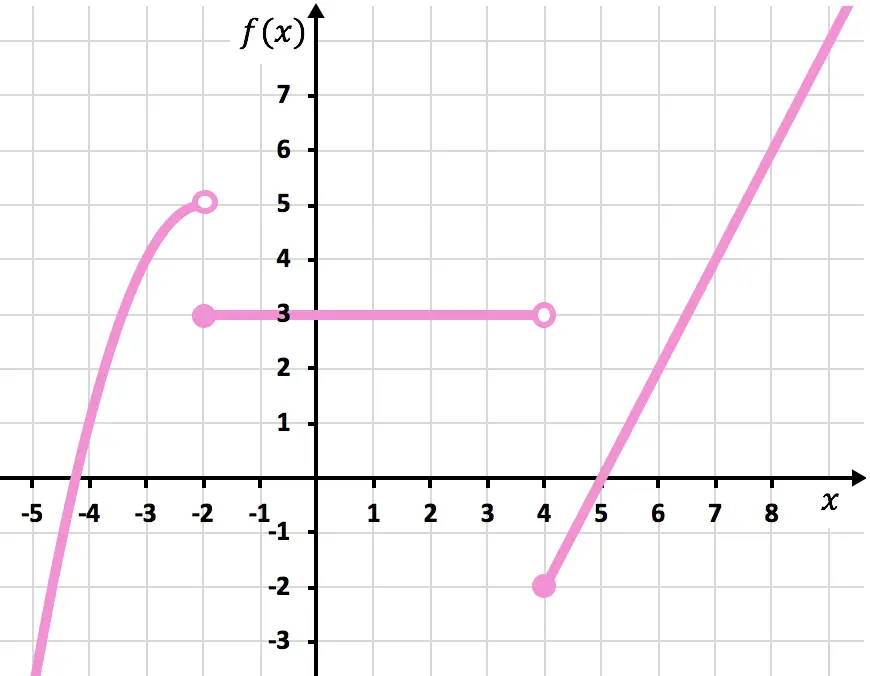
Los límites laterales no coinciden en el punto x=-2, por la izquierda la función se va aproximando a f(x)=5 y, en cambio, por la derecha la función es constante y vale 3.

Los límites laterales también son distintos cuando x tiende a 4. La función a trozos tiende a 3 por la izquierda, pero por la derecha tiende a -2.

 

Ejercicio 2

Determina si existe el límite cuando x tiende a 3 de la siguiente función definida a trozos y, en tal caso, cuál es su valor.

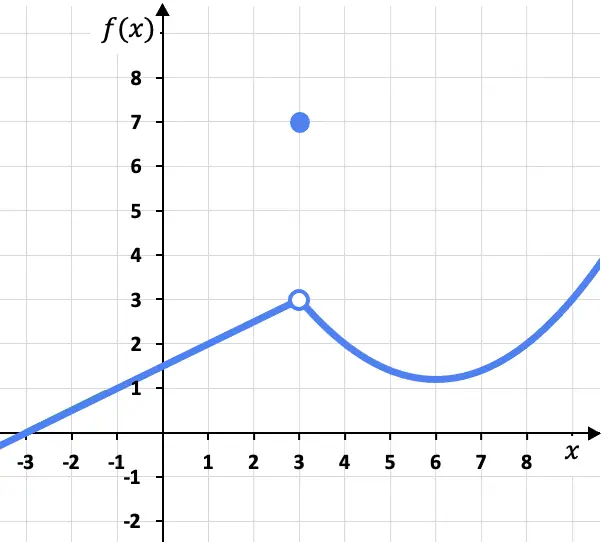
En este problema, los límites laterales en el punto x=3 por la izquierda y por la derecha son idénticos, ya que la función se aproxima al mismo valor (f(x)=3) tanto si nos acercamos por su lado izquierdo como por su lado derecho:

Por tanto, según la definición matemática de límite, el límite de la función cuando x tiende a 3 es igual a 3, porque los dos límites laterales en ese mismo punto coinciden en ese valor:

Aunque el límite de la función en x=3 sea 3, hay que tener en cuenta que la función en ese punto no vale 3, sino que f(3)=7. Como veremos más adelante, esto significa que la función no es continua en x=3, sino que tiene una discontinuidad evitable.

 

Ejercicio 3

Calcula los límites laterales de la siguiente función racional en el punto x=4.

Para calcular el límite cuando x tiende a 4 por la izquierda tomamos un valor más pequeño que 4 pero muy cercano a él, por ejemplo 3,999:

Así que el límite lateral cuando x tiende a 4 por la izquierda es más infinito.

Y para resolver el límite cuando x tiende a 4 por la derecha evaluamos la función en un valor más grande que 4 pero muy próximo a él, por ejemplo 4,001:

Por lo que el límite lateral cuando x tiende a 4 por la derecha es menos infinito.

 

Ejercicio 4

Calcula el límite, si existe, de la siguiente función definida a trozos en el punto x=2:

En este caso, el enunciado del problema nos pide calcular el límite donde la función a trozos cambia de expresión, de manera que debemos hallar el límite lateral por la izquierda utilizando la primera expresión y el límite lateral por la derecha usando la segunda expresión.

El límite de la función en x=2 por la izquierda coincide con el límite de la función por la derecha, por tanto, el límite de la función existe y vale 1: