Composición de funciones (función compuesta)

En este post explicamos qué es la función compuesta (o composición de funciones). Además, podrás ver varios ejemplos de funciones compuestas y cómo se calcula el dominio de este tipo de funciones. Finalmente, encontrarás las propiedades de la composición de funciones y varios ejercicios resueltos paso a paso para practicar.

¿Qué es la composición de funciones?

La composición de funciones consiste en evaluar un mismo valor de la variable independiente (x) en dos funciones o más de manera sucesiva. Por ejemplo, la composición de funciones (g o f)(x) da como resultado la función compuesta g[f(x)].

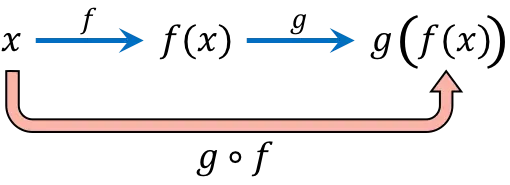
composicion de funciones

La expresión de la función compuesta g\circ f se lee «f compuesta con g» o «f seguida de g».

Ten en cuenta que el orden es importante en la composición de funciones, primero se aplica la función que está a la derecha del símbolo de composición (f) y luego la función que está a la izquierda del símbolo de composición (g).

Ejemplo de composición de funciones

Vista la definición de función compuesta, vamos a ver un ejemplo de cómo calcular la composición de dos funciones.

  • Dadas las siguientes dos funciones diferentes:

f(x)=3x+1 \qquad g(x)=\cfrac{x+4}{2}

Calcula la función compuesta \left(g \circ f\right)(x) y evalúala en x=3.

La composición de funciones \left(g \circ f\right)(x) significa que debemos hacer la siguiente función compuesta:

\left(g \circ f\right)(x) = g\Big(f(x)\Big)

Para resolverla, sustituimos f(x) por su expresión algebraica:

g\Big(f(x)\Big)= g\Big(3x+1\Big)

Y ahora cogemos la función de g(x)=\cfrac{x+4}{2}  y ponemos la expresión 3x+1 donde haya una x:

g\Big(3x+1\Big)=\cfrac{(3x+1)+4}{2}=\cfrac{3x+5}{2}

De esta manera ya hemos calculado la función f compuesta con g:

\left(g \circ f\right)(x)=\cfrac{3x+5}{2}

Finalmente, para evaluar la función compuesta en x=3 simplemente debemos calcular la imagen de la función en dicho valor:

\left(g \circ f\right)(3)=\cfrac{3\cdot 3+5}{2}=\cfrac{14}{2}=7

Dominio de la función compuesta

Normalmente, cuando hacemos operaciones con funciones, el dominio de la función resultante es la intersección de los dominios de las funciones originales. Sin embargo, esta propiedad no se cumple con la composición de funciones.

El dominio de la composición de funciones (g\circ f)(x) equivale al conjunto de todos los valores de x en el dominio de la función f tal que f(x) pertenece al dominio de la función g.

\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}

Por lo tanto, para calcular el dominio de una función compuesta, primero debes hallar el dominio de cada función por separado, y luego el dominio de la función resultante de la operación. De modo que el dominio de la composición de funciones serán todos aquellos valores que cumplan la condición matemática anterior.

👉 ¡Recuerda que si tienes algún problema que no sabes resolver nos lo puedes preguntar abajo en los comentarios!

Propiedades de la composición de funciones

Las funciones compuestas tienen las siguientes características:

  • La composición de funciones posee la propiedad asociativa, por lo tanto, siempre se cumple la siguiente ecuación:

f\circ (g\circ h)=(f\circ g)\circ h

  • En general, la composición de funciones no es conmutativa, por lo que el orden de la operación condiciona el resultado:

f\circ g\neq g\circ f

  • El elemento neutro de la composición de funciones corresponde a la función identidad f(x)=x. De manera que cualquier función compuesta con la función identidad da como resultado la propia función:

f\circ id = id \circ f = f

id = x

  • Calcular la inversa de la composición de dos funciones es igual a primero hallar la inversa de cada función y luego determinar la función compuesta:

(f\circ g)^{-1}=f^{-1}\circ g^{-1}

  • La función inversa también actúa como elemento simétrico de la función compuesta, ya que la composición de una función con su inversa es equivalente a la función identidad:

(f\circ f^{-1})^{-1}=(f^{-1}\circ f)=id=x

  • La derivada de la composición de dos funciones se calcula utilizando la regla de la cadena:

\bigl(g\circ f\bigr)'(x)=g'\Bigl(f(x)\Bigr)\cdot f'(x)

➤ Ver: ¿qué es la regla de la cadena?

Ejercicios resueltos de la composición de funciones

Ejercicio 1

Dadas las siguientes dos funciones:

f(x)=x-2 \qquad g(x)= 5x + 4

Calcula las composiciones de funciones f compuesta con g y g compuesta con f.

(g\circ f)(x)

(f\circ g)(x)

La composición de funciones \left(g \circ f\right)(x) significa calcular la siguiente función compuesta:

\left(g \circ f\right)(x) = g\Big(f(x)\Big)

Así que, para resolverla, sustituimos f(x) por su expresión: f(x)=x-2

g\Big(f(x)\Big)= g\Big(x-2\Big)

Y g\Big(x-2\Big) quiere decir que en la expresión de g(x) =5x+4  debemos sustituir la variable x por x-2:

g\Big(x-2\Big) = 5(x-2) +4= 5x-10+4 = 5x-6

Por tanto:

\bm{\left(g \circ f\right)(x) = 5x-6}

Por otra parte, para hallar la función g compuesta con f debemos hacer el mismo procedimiento pero con el orden invertido:

\begin{aligned}\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&=f\Big(5x+4\Big)\\[2ex]&=(5x+4)-2\\[2ex]&=\bm{5x+2}\end{aligned}

Con este ejercicio también queda demostrada la propiedad de que las funciones compuestas no son conmutativas, ya que el resultado depende del orden en el que se aplican las funciones.

 

Ejercicio 2

Dadas las siguientes dos funciones:

\displaystyle f(x) =x^2-3 \qquad g(x)=\frac{2x+3}{x+4}

Calcula la composición de funciones f compuesta con g.

(g\circ f)(x)

La función f compuesta con g significa resolver la siguiente función compuesta:

\left(g \circ f\right)(x) = g\Big(f(x)\Big)

Así que sustituimos la función f(x) por su expresión:

g\Big(f(x)\Big)= g\Big(x^2-3 \Big)

Y ahora debemos sustituir x por x^2-3 en la expresión de la función g(x):

\begin{aligned}g\Big(x^2-3\Big)&=\cfrac{2(x^2-3)+3}{(x^2-3)+4}\\[2ex]&=\cfrac{2x^2-6+3}{x^2+1}\\[2ex]&=\cfrac{2x^2-3}{x^2+1}\end{aligned}

En definitiva, el resultado de la composición de funciones es:

\bm{\left(g \circ f\right)(x) =} \cfrac{\bm{2x^2-3}}{\bm{x^2+1}}

 

Ejercicio 3

Dadas las siguientes dos funciones cuadráticas:

\displaystyle f(x) =x^2 \qquad g(x)=g(x)= x^2-4x+8

Determina el resultado de la siguiente composición de funciones:

(g\circ f)(2)

\left(g \circ f\right)(2) implica hallar la siguiente función compuesta:

\left(g \circ f\right)(2) = g\Big(f(2)\Big)

Así que para resolver la función compuesta primero calculamos f(2) :

f(x)=x^2

f(2)=2^2=4

Por tanto, como f(2)=4 :

\left(g \circ f\right)(2) = g\Big(f(2)\Big) = g\big(4\big)

Así que para hallar el valor de la función compuesta simplemente debemos calcular g(4) :

\begin{aligned}\left(g \circ f\right)(2)&=g\Big(f(2)\Big)\\[2ex]&= g\big(4\big)\\[2ex]&=4^2-4\cdot 4+8 \\[2ex]&= 16 - 16 + 8\\[2ex]&= 8\end{aligned}

En resumen, el resultado del problema de composición de funciones es:

\bm{\left(g \circ f\right)(2) =8}

 

Ejercicio 4

Dadas las siguientes dos funciones:

\displaystyle f(x)=\frac{2x-2}{-x+7}\qquad g(x)= x^2-1

Halla el resultado de g compuesta con f en x=2:

(f\circ g)(2)

En este caso, debemos calcular la siguiente función compuesta:

\left(f \circ g\right)(2) = f\Big(g(2)\Big)

Entonces, primero hallamos g(2) :

g(x)=x^2-1

g(2)=2^2-1=4-1 = 3

Y, por tanto, como g(2)=3 :

\left(f \circ g\right)(2) = f\Big(g(2)\Big) = f\big(3\big)

Así que para resolver la función compuesta tenemos que calcular f(3) :

\begin{aligned}\left(f \circ g\right)(2)&=f\Big(g(2)\Big)\\[2ex]&= f\big(3\big)\\[2ex]&=\cfrac{2\cdot 3-2}{-3+7}\\[2ex]&=\cfrac{6-2}{-3+7}\\[2ex]&=\cfrac{4}{4}\\[2ex]&=1\end{aligned}

En conclusión, el resultado del ejercicio de funciones compuestas es:

\bm{\left(f \circ g\right)(2)=1}

 

Ejercicio 5

Dadas las siguientes tres funciones:

f(x) = x+1 \qquad g(x)= 3x - 5\qquad h(x) = \sqrt{x} - 3

Calcula la siguiente composición de las 3 funciones:

(h \circ g \circ f )(x)

La expresión \left(h \circ g \circ f\right)(x) significa que debemos calcular la siguiente función compuesta:

\left(h \circ g \circ f\right)(x) = h \bigg( g\Big(f(x)\Big) \bigg)

Así que primero determinamos g\Big( f(x)\Big):

\begin{aligned}g\Big( f(x)\Big)&=g\Big(x+1 \Big)\\[2ex]&= 3(x+1)-5\\[2ex]&= 3x+3-5\\[2ex]&= 3x-2\end{aligned}

Y ahora calculamos h \bigg( g\Big(f(x)\Big) \bigg) . Para ello, sustituimos la expresión hallada de g\Big(f(x)\Big) donde aparezca una x en la función h(x):

\begin{aligned}h \bigg( g\Big(f(x)\Big) \bigg)&= h \bigg(3x-2\bigg)\\[2ex]&= \sqrt{3x-2} - 3\end{aligned}

No podemos simplificar más la función compuesta. Por tanto la composición de las tres funciones da como resultado una función irracional:

\bm{\left(h \circ g \circ f\right)(x) =\sqrt{3x-2} - 3 }

 

4 comentarios en “Composición de funciones (función compuesta)”

  1. Amado Edward

    INTERESANTE LAS INDICACIONES DEL DESARROLLO DE COMPOSICIÓN DE FUNCIIONES, POR LO QUE QUEDO MUY AGRADECIDO DEL DESARROLLO DE LOS EJERCICIOS.
    GRACIAS

    Responder

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *