Regla de la cadena (derivadas)

Aquí encontrarás qué es la regla de la cadena y cómo derivar funciones utilizando la regla de la cadena. Además, podrás ver varios ejemplos de derivadas resueltas con la regla de la cadena e, incluso, podrás practicar con ejercicios resueltos paso a paso de derivadas aplicando la regla de la cadena.

¿Qué es la regla de la cadena?

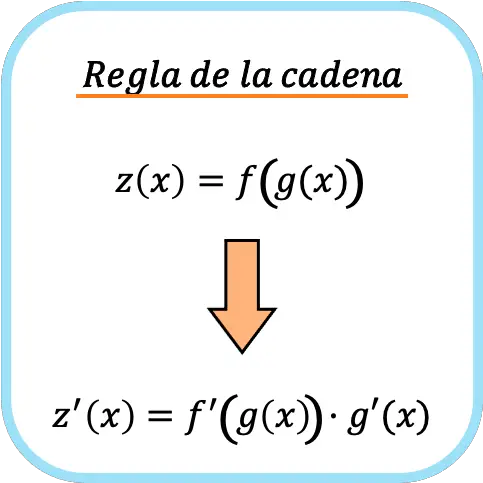
La regla de la cadena es una fórmula que sirve para derivar funciones compuestas. La regla de la cadena establece que la derivada de una función compuesta f(g(x)) es igual a la derivada f'(g(x)) multiplicada por la derivada g'(x).

regla de la cadena

➤ Ver: función compuesta

De manera informal, se suele decir que la regla de la cadena consiste en derivar la función y luego multiplicar por lo de dentro.

La fórmula de la regla de la cadena nos facilita mucho la derivación de funciones compuestas, ya que si tuviéramos que derivar una composición de funciones utilizando el límite de la definición de derivada tendríamos que hacer muchos cálculos.

Por otro lado, hay que tener en cuenta que esta regla solo sirve para hallar la derivada de funciones compuestas, no de cualquier tipo de función ni de operaciones con funciones. Por ejemplo, un fallo muy común es confundirse y aplicar la regla de la cadena en productos de funciones como el siguiente:

\ln(x)\cdot x^2 ❌

La regla de la cadena solamente se puede utilizar cuando tenemos una función dentro de otra.

\ln(x^2) ✅

Ejemplos de derivadas con la regla de la cadena

Vista la definición de la regla de la cadena, vamos a derivar varias funciones con la regla de la cadena a modo de ejemplo. ¡Recuerda que si en algún ejemplo no entiendes cómo se deriva la función con la regla de la cadena puedes preguntarnos en los comentarios!

Ejemplo 1

En este ejemplo utilizaremos la regla de la cadena para derivar el logaritmo natural de x al cuadrado:

f(x)=\ln(x^2)

La derivada del logaritmo neperiano es 1 partido por su argumento, por tanto, la derivada f'\bigl(g(x)\bigr) será:

f(x)=\ln(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{u}

f\bigl(g(x)\bigr)=\ln(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=\cfrac{1}{x^2}

Por otro lado, la derivada de x elevada a dos es 2x:

g(x)=x^2\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=2x

Finalmente, calculamos la derivada de toda la función aplicando la regla de la cadena. La derivada de la función compuesta será el producto de las dos derivadas que acabamos de encontrar:

z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

f(x)=\ln(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{x^2}\cdot 2x = \cfrac{2x}{x^2}=\cfrac{2}{x}

Ejemplo 2

En este segundo ejemplo derivaremos una función potencial que tiene como base un polinomio:

f(x)=\left(3x^2+4x-5\right)^3

Para derivar una potencia tenemos que poner delante el exponente original y restar una unidad en el exponente, por lo que la derivada de la función potencial sin aplicar la regla de la cadena sería:

f\bigl(g(x)\bigr)=\left(3x^2+4x-5\right)^3 \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=3\left(3x^2+4x-5\right)^2

Ahora derivamos lo de dentro del paréntesis:

g(x)=3x^2+4x-5\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=6x+4

Y, por último, empleamos la regla de la cadena para resolver la derivada de toda la función, que será la multiplicación de las dos derivadas calculadas anteriormente:

z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

f(x)=\left(3x^2+4x-5\right)^3 \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=3\left(3x^2+4x-5\right)^2\cdot (6x+4)

Ejemplo 3

En este caso resolveremos la derivada del seno de x al cubo más 7x:

f(x)=\text{sen}(x^3+7x)

Efectivamente, se trata de una composición de funciones porque tenemos la función x3+7x dentro de la función seno, por lo tanto, podemos usar la regla de la cadena para hallar la derivada de la función compuesta.

Por una parte, la derivada del seno es el coseno, por lo que la derivada de la función de afuera será el coseno con el mismo argumento del seno:

f\bigl(g(x)\bigr)=\text{sen}(x^3+7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=\text{cos}(x^3+7x)

Y, por otra parte, la derivada de x3+7x es 3x2+7.

g(x)=x^3+7x\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=3x^2+7

Por lo tanto, la derivada de la función compuesta es el producto de ambas derivadas:

z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

f(x)=\text{sen}(x^3+7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cos}(x^3+7x)\cdot (3x^2+7)

Ejercicios resueltos de derivadas con la regla de la cadena

Ejercicio 1

Deriva la siguiente función compuesta utilizando la regla de la cadena:

f(x)=\left(5x^2-6x\right)^3

La función de fuera es una función potencial, así que para calcular su derivada debemos aplicar la siguiente fórmula:

f\bigl(g(x)\bigr)=a\bigl(g(x)\bigr)^n \ \longrightarrow \ f'\bigl(g(x)\bigr)=n\cdot a\bigl(g(x)\bigr)^{n-1}

f\bigl(g(x)\bigr)=\left(5x^2-6x\right)^3\ \longrightarrow \ f'\bigl(g(x)\bigr)= 3\left(5x^2-6x\right)^2

Y luego calculamos la derivada de la función de dentro. Se trata de una resta de potencias, por lo que para calcular su derivada tenemos que aplicar la siguiente fórmula a cada uno de sus términos:

f(x)=ax^n \ \longrightarrow \ f'(x)=n\cdot ax^{n-1}

g(x)=5x^2-6x\ \longrightarrow  g'(x)=2\cdot 5x^1-1 \cdot 6 x^0 =10x-6

En definitiva, la derivada de la función compuesta es el producto de las dos derivadas halladas:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

f(x)=\left(5x^2-6x\right)^3 \ \longrightarrow \ \bm{f'(x)= 3\left(5x^2-6x\right)^2\cdot (10x-6)}

 

Ejercicio 2

Resuelve la derivada de la siguiente función compuesta utilizando la regla de la cadena:

f(x)=-3\left(5x^5+9x^3\right)^4

En primer lugar, hallamos la derivada de la función exterior:

\begin{aligned} f\bigl(g(x)\bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr) & =4 \cdot ( -3) \left(5x^5+9x^3\right)^3 \\[1.5ex]&=-12\left(5x^5+9x^3\right)^3 \end{aligned}

Y ahora resolvemos la derivada de la función del interior:

g(x)=5x^5+9x^3\ \longrightarrow \ g'(x)=25x^4+27x^2

Así que la derivada de toda la función es:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

f(x)=-3\left(5x^5+9x^3\right)^4 \ \longrightarrow \ \bm{f'(x)=-12\left(5x^5+9x^3\right)^3\cdot \left(25x^4+27x^2\right)}

 

Ejercicio 3

Calcula la derivada de la siguiente composición de funciones con la regla de la cadena:

f(x)=e^{2x^3}

Se trata de una función exponencial, por tanto, para calcular su derivada debemos aplicar la siguiente fórmula:

f(x)=e^{x} \ \longrightarrow \ f'(x)=e^{x}

f\bigl(g(x)\bigr)=e^{2x^3} \ \longrightarrow \ f'\bigl(g(x)\bigr)= e^{2x^3}

Derivamos también la función del exponente de la función:

g(x)=2x^3 \ \longrightarrow \ g'(x)=6x^2

Y usamos la regla de la cadena para hallar la derivada de toda la función compuesta:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

f(x)=e^{2x^3} \ \longrightarrow \ \bm{f'(x)= e^{2x^3}\cdot 6x^2}

 

Ejercicio 4

Halla la derivada de la siguiente función compuesta mediante la regla de la cadena:

f(x)=\sqrt[3]{\text{sen}(x) +x }

Se trata de una composición de funciones, porque tenemos un seno y una función lineal en el argumento de una función irracional. Así que primero calculamos la derivada de la raíz:

f(x)=\sqrt[n]{x} \ \longrightarrow \ f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}

f\bigl(g(x)\bigr)=\sqrt[3]{\text{sen}(x) +x } \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }}

Y ahora derivamos el argumento del radical. Se trata de una suma de funciones, por lo tanto, la derivada será la suma de la derivada de cada término:

g(x)=\text{sen}(x) +x \ \longrightarrow \ g'(x)=\cos(x) + 1

De forma que la derivada de toda la función es igual a la multiplicación de las dos derivadas calculadas:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

\begin{aligned}f(x)=\sqrt[3]{\text{sen}(x)+x} \ \longrightarrow \ f'(x)& = \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }} \cdot \bigl(\cos(x) + 1 \bigr)\\[1.5ex]&=\cfrac{\bm{\cos(x) + 1}}{\bm{3\sqrt[3]{\bigl(\mathbf{sen}(x) +x\bigr)^2} }}\end{aligned}

 

Ejercicio 5

Deriva la siguiente composición de funciones mediante la regla de la cadena:

f(x)=3^{x^2+5}

Para aplicar la regla de la cadena, debemos encontrar la derivada de la potencia y del polinomio y luego multiplicarlas. Así pues, derivamos la potencia utilizando la fórmula correspondiente:

f(x)=a^x \ \longrightarrow \ f'(x)=a^x\cdot \ln (a)

f\bigl(g(x)\bigr)=3^{x^2+5} \ \longrightarrow \ f'\bigl(g(x)\bigr)= 3^{x^2+5}\cdot \ln(3)

En segundo lugar, derivamos la función polinómica del exponente:

g(x)=x^2+5 \ \longrightarrow \ g'(x)=2x

Y la regla de la cadena nos dice que derivada de toda la función es el producto de las derivadas que acabamos de encontrar:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

f(x)=3^{x^2+5} \ \longrightarrow \ \bm{f'(x)= 3^{x^2+5}\cdot \ln(3) \cdot 2x}

 

Ejercicio 6

f(x)=\ln \bigl(4x^2 \cdot \cos(x) \bigr)

Evidentemente la función de este problema es compuesta, ya que en el argumento del logaritmo natural tenemos un producto de dos tipos de funciones diferentes. Entonces primero derivamos el logaritmo:

f(x)=\ln(x) \ \longrightarrow \ f'(x)=\cfrac{1}{x}

f\bigl(g(x)\bigr)=\ln \bigl(4x^2 \cdot \cos(x) \bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{4x^2 \cdot \cos(x) }

En segundo lugar, derivamos la función del argumento del logaritmo. Se trata de una multiplicación de dos funciones, por lo que debemos utilizar la siguiente fórmula para hacer la derivación:

z(x)=f(x) \cdot g(x) \ \longrightarrow \ z'(x)=f'(x)\cdot g(x)+f(x) \cdot g'(x)

\begin{aligned}g(x)=4x^2 \cdot \cos(x) \ \longrightarrow \ g'(x) & = 8x\cdot \cos(x) + 4x^2 \cdot \bigl(- \text{sen}(x)\bigr) \\[2ex] & = 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x)\end{aligned}

De modo que la derivada de toda la función, según la regla de la cadena, será el producto de las dos derivadas:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

\begin{aligned}f'(x)&= \cfrac{1}{4x^2 \cdot \cos(x) } \cdot \bigl( 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x) \bigr)\\[1.5ex]&=\cfrac{8x\cdot \cos(x) - 4x^2 \cdot\text{sen}(x)}{4x^2 \cdot \cos(x)}\\[1.5ex]&=\cfrac{\bm{2\cos(x) - x \cdot }\mathbf{sen}\bm{(x)}}{\bm{x \cdot \cos(x) }}\end{aligned}

 

Ejercicio 7

Resuelve la derivada de la siguiente función aplicando la regla de la cadena:

f(x)=\log_9 (e^{x^2}-6x^7)

Es una composición de funciones, por tanto, derivaremos el logaritmo y su argumento por separado y luego multiplicaremos las derivadas.

Así pues, primero derivamos el logaritmo en base 9:

f(x)=\log_a (x) \ \longrightarrow \ f'(x)=\cfrac{1}{x\cdot \ln (a)}

f\bigl(g(x)\bigr)=\log_9 (e^{x^2}-6x^7) \ \longrightarrow \ f'\bigl(g(x)\bigr)=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}

Y ahora calculamos la derivada del argumento del logaritmo. Fíjate que el número e tiene una función en su argumento, es decir, es una función compuesta, por tanto, también tenemos que aplicar la regla de la cadena para derivar esta función:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

h(x)=e^{x^2} \ \longrightarrow \ h'(x)=e^{x^2}\cdot \bigl(x^2\bigr)' =e^{x^2}\cdot 2x

De manera que la derivada de todo el argumento del logaritmo será:

g(x)= e^{x^2}-6x^7\ \longrightarrow \ g'(x)=e^{x^2}\cdot 2x - 42x^6

Y, finalmente, la derivada de toda la función será el producto de f'(g(x)) y g'(x):

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

\begin{aligned}f'(x)&=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)} \cdot \bigl(e^{x^2}\cdot 2x - 42x^6\bigr)\\[1.5ex]&=\cfrac{\bm{e^{x^2}\cdot 2x - 42x^6}}{\bm{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}}\end{aligned}

 

Ejercicio 8

Deriva la siguiente función compuesta usando la regla de la cadena:

f(x)=\text{sen}\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)

En este ejercicio tenemos una composición de varias funciones, de modo que tendremos que aplicar varias veces la regla de la cadena. Primero derivamos la función trigonométrica del seno, cuya derivada es el coseno:

f\bigl(g(x)\bigr)=\text{sen}\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)\ \longrightarrow \ f'\bigl(g(x)\bigr)=\cos\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)

Y ahora calculamos la derivada del argumento del seno utilizando la regla de la cadena:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

\begin{aligned} g(x)= \Bigl( 9x^5 + \cos(x) \Bigr)^2 \cdot g'(x) &= 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(9x^5 + \cos(x) \Bigr)' \\[1.5ex]&=2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-\text{sen}(x)\Bigr)\end{aligned}

Finalmente, la derivada de toda la composición de funciones la obtenemos aplicando otra vez la regla de la cadena:

z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

\bm{f'(x)=\cos } \bm{\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr) \cdot 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-}\mathbf{sen}\bm{(x)\Bigr)}

 

Demostración de la regla de la cadena

Por último, vamos a demostrar la fórmula de la regla de la cadena. Para ello, partiremos de la definición matemática de una derivada:

\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}

Sea z una función compuesta por dos funciones:

z=f\bigl(g(x)\bigr)

Entonces la derivada de la función z aplicando la definición sería:

\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{h}

Como ya sabes, podemos multiplicar y dividir una fracción por un mismo término, porque esto no modifica el resultado. De manera que podemos hacer el siguiente paso:

\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{h}\cdot \frac{g(x+h)-g(x)}{g(x+h)-g(x)}

Reordenamos los denominadores de las fracciones:

\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{g(x+h)-g(x)}\cdot \frac{g(x+h)-g(x)}{h}

Aplicando las propiedades de los límites, podemos separar el límite anterior en dos. Ya que el límite de un producto es igual al producto de los límites:

\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{g(x+h)-g(x)}\cdot \lim_{h \to 0}\frac{g(x+h)-g(x)}{h}

Y esta expresión es equivalente a la siguiente:

\displaystyle z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)

De modo que queda demostrada la fórmula de la regla de la cadena, ya que hemos llegado a ella a partir de la definición de la derivada.

10 comentarios en “Regla de la cadena (derivadas)”

    1. Funciones

      Buenas Zaryox,

      Tenías razón, en el último paso, al dividir el 8 entre 4 debería poner un 2, y no un 4. Ya se ha corregido, ¡muchas gracias por avisar! 🙂

  2. FelipeKLK_fumaMALEKELE

    Buenos días.
    Me ha encantado la página, tiene muchos ejercicios muy interesantes y variados. Gracias por la ayuda!😀

    Responder
  3. sabio arcangel chinchay suarez

    Hola, muy buena información, me está ayudando bastante a poder entender este tema en la universidad.

    Responder
  5. Meli

    Hola! En el ejercicio 6, no queda claro el último paso: el 8 se divide por 4x al cuadrado y queda 2. cos (x), pero los otros dos 4 x al cuadrado uno es seno y el de abajo cos. el de arriba el 4x al cuadrado debe quedar. O no?
    Gracias!

    Responder
    1. Funciones

      Hola Meli,

      La derivada está bien resuelta.

      En el numerador hay dos términos 8x\text{cos}(x) y 4x^2\text{sen}(x), por otro lado, en el denominador está el término 4x^2\text{cos}(x). Todos estos términos tienen en común una x y que son divisibles por 4, por lo tanto, la fracción se simplifica dividiendo todos los términos por x y por 4:

      \cfrac{8x\cdot \cos(x) - 4x^2 \cdot\text{sen}(x)}{4x^2 \cdot \cos(x)}\ \longrightarrow \ \cfrac{2\cos(x) - x \cdot\text{sen}(x)}{x \cdot \cos(x)}

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *