Funciones acotadas

En este post explicamos qué son las funciones acotadas (superiormente e inferiormente). Además, te mostramos qué significa que una función esté acotada en un punto y, finalmente, encontrarás las propiedades de este tipo de funciones.

¿Qué es una función acotada?

Una función acotada es una función cuya gráfica está dentro de unas cotas. Es decir, una función está acotada superiormente si existe un número K tal que no hay ningún valor de la función que sea superior a K (f(x)≤K), y una función está acotada inferiormente si existe un número K tal que es inferior a todos los valores de la función (f(x)≥K). Por lo tanto, una función acotada es una función que está acotada superiormente e inferiormente.

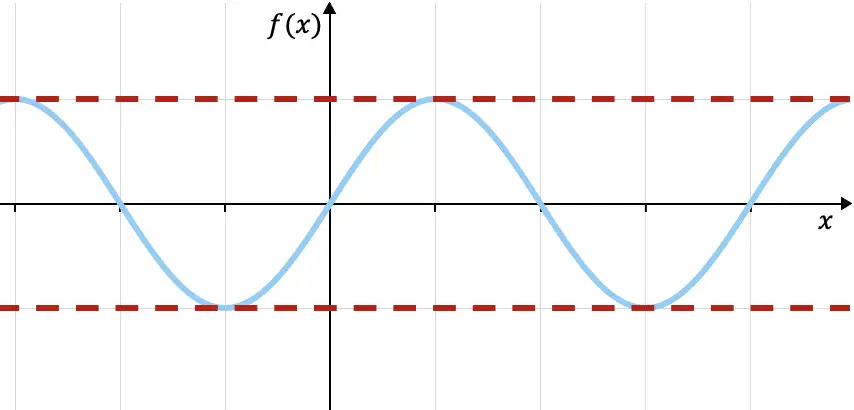
Por ejemplo, la función trigonométrica del seno, representada gráficamente arriba, está acotada superiormente por f(x)=1 y está acotada inferiormente por f(x)=-1 (rectas discontinuas de color rojo), ya que todos los valores de la función están dentro de estas dos cotas. Puedes ver más propiedades de esta función en el siguiente enlace:

➤ Ver: Características de la función seno

Función acotada superiormente

Sin embargo, no todas las funciones están acotadas superiormente y inferiormente, sino que una función puede estar solamente acotada por arriba o por abajo.

Las funciones acotadas superiormente son aquellas que no superan un determinado valor, es decir, se cumple la siguiente condición:

Donde el valor K es la cota superior de la función.

Por ejemplo, la siguiente parábola está acotada superiormente por K=7, pero la función no está acotada inferiormente ya que sus ramas se van alargando hasta el infinito.

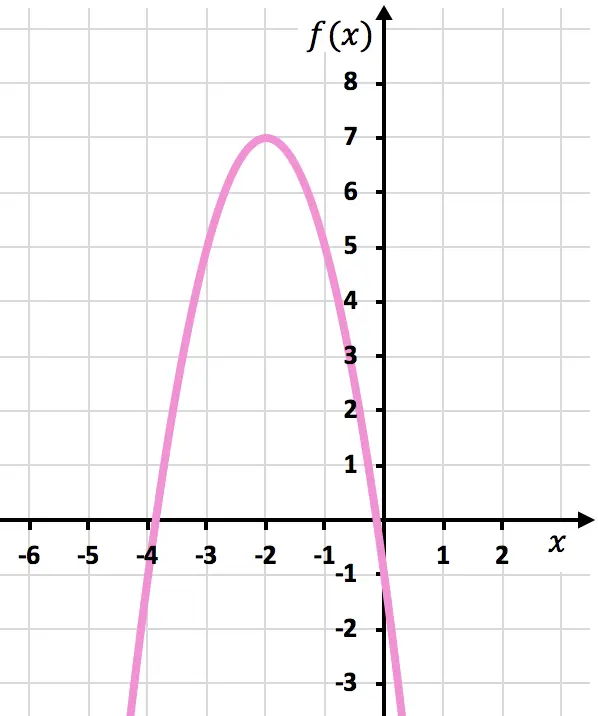
Lógicamente, si la función está acotada por K=7, también está acotada por K=8 y por valores mayores.

A la cota superior más pequeña se le llama extremo superior y se representa por sup(f). Además, si la función alcanza dicho extremo superior dentro de su dominio, diremos que ese punto es el máximo absoluto de la función.

➤ Ver: ¿qué son los máximos y los mínimos de una función?

En nuestro caso, la función está acotada geométricamente por K=7, por tanto, ese es el extremo superior y el máximo absoluto de la función.

Función acotada inferiormente

Las funciones acotadas inferiormente son aquellas que no tienen ningún valor inferior a un determinado número, es decir, verifican la siguiente expresión matemática:

Donde el valor K es la cota inferior de la función.

A continuación tienes la representación gráfica de una función exponencial que está acotada inferiormente por K=3:

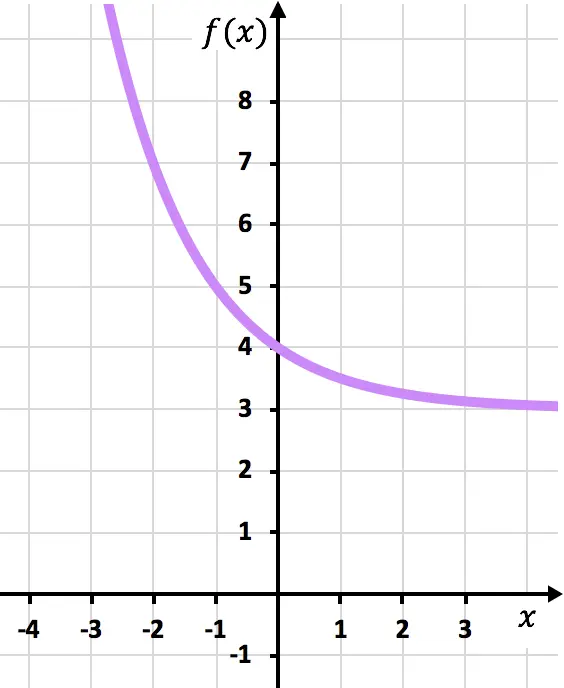
Evidentemente, la función también está acotada por valores menores que K=3.

Igual que antes, a la cota inferior más grande se le llama extremo inferior y se representa con inf(f). Además, si la función alcanza dicho extremo inferior dentro de su dominio, diremos que ese punto es el mínimo absoluto de la función.

En este caso, K=3 no es el mínimo absoluto de la función, porque la función alcanza dicho valor en el infinito y, por tanto, está fuera de su dominio. O dicho con otras palabras, f(x)=3 es una asíntota horizontal de la función.

Existe un teorema que permite saber si una función está acotada superiormente e inferiormente sin su representación gráfica. Haz click aquí para ver en qué consiste el teorema de Weierstrass.

➤ Ver: teorema de Weierstrass

Función acotada en un punto

Acabamos de estudiar el concepto de acotación de una función en general, pero también se puede analizar si una función está acotada o no en un entorno más pequeño, es decir, en una parte de la función.

Si es un punto dentro del dominio de la función y un valor cualquiera, diremos que la función está acotada superiormente/inferiormente en el punto si existe un entorno por el que la función está acotada superiormente/inferiormente.

Por lo tanto, una función está acotada en el punto si está acotada superiormente e inferiormente en un entorno

Obviamente, si una función está acotada de manera general, también estará acotada en cada una de sus puntos. Sin embargo, el recíproco es falso, es decir, una función puede estar acotada en cada uno de sus puntos y no ser una función acotada en todo su dominio.

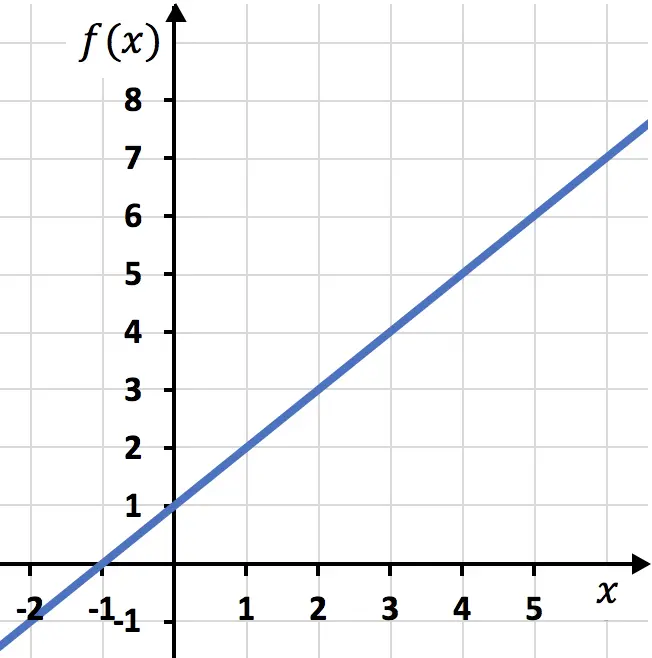
Por ejemplo, la siguiente función afín está acotada parcialmente en cada uno de sus puntos, pero no es una función acotada.

Propiedades de las funciones acotadas

Las funciones acotadas tienen las siguientes propiedades:

• Si y son dos funciones acotadas, la suma (o resta) de las dos funciones también es una función acotada.
• Si y son dos funciones acotadas, el producto de las dos funciones también resulta ser una función acotada.
• Si una función tiene una asíntota vertical, no puede estar acotada totalmente. Por contra, la función puede estar acotada superior o inferiormente.
• Toda función continua y acotada en un intervalo es integrable.