Asíntota horizontal

En este post te explicamos qué son las asíntotas horizontales de una función y cómo se calculan. También, encontrarás varios ejemplos de este tipo de asíntotas para entender completamente el concepto y, además, podrás practicar con ejercicios resueltos de asíntotas horizontales.

¿Qué es una asíntota horizontal?

Una asíntota horizontal de una función es una recta horizontal a la cual su gráfica se va aproximando indefinidamente sin llegar nunca a cruzarla. Por lo tanto, la ecuación de una asíntota horizontal es y=k, donde k es el valor de la asíntota horizontal.

Es decir, k es una asíntota horizontal si el límite de la función cuando x tiende a infinito es igual a k.

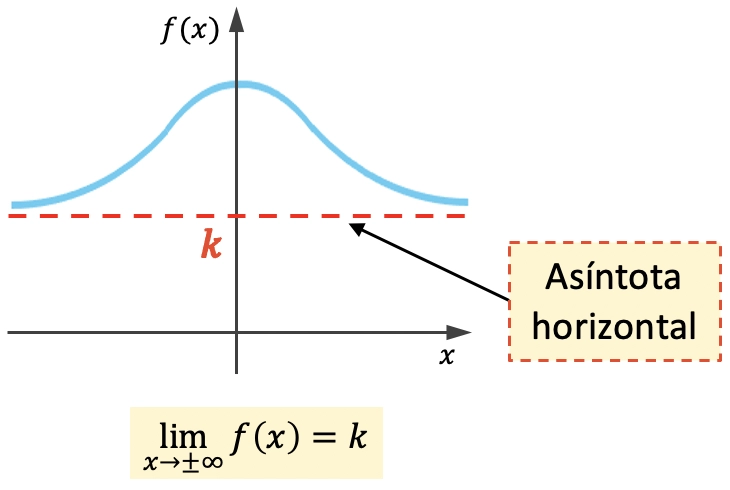
asintota horizontal de una funcion

La función anterior tiene una asíntota horizontal por los dos lados de la gráfica, pero una función puede tener una asíntota horizontal por un solo lado:

  • La función tiene una asíntota horizontal por la izquierda si el límite al menos infinito da un número real.
  • La función tiene una asíntota horizontal por la derecha si el límite al más infinito da un número real.
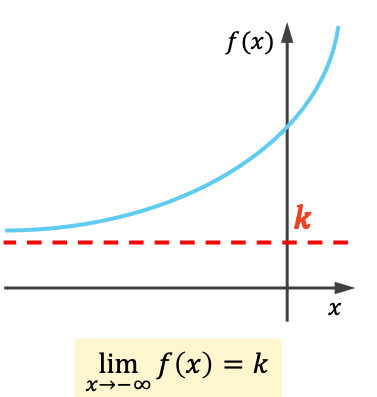
asintota horizontal de una funcion por la izquierda
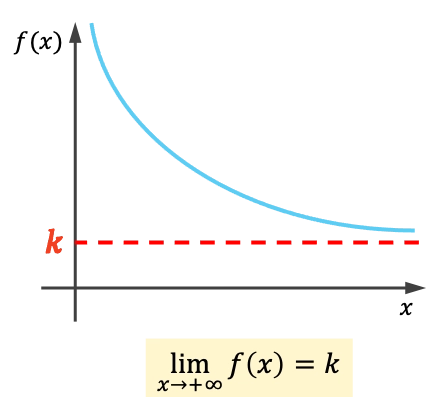
asintota horizontal por la derecha

Cómo calcular la asíntota horizontal de una función

Para calcular la asíntota horizontal de una función, se deben seguir los siguientes pasos:

  1. Calcular el límite de la función en los infinitos (+∞ y -∞).
  2. Si algún límite en el infinito da un número real (k), la recta y=k es una asíntota horizontal de la función.
  3. Si ninguno de los dos límites da como resultado un número real, la función no tiene asíntotas horizontales.

Ejemplo de asíntota horizontal

Para que puedes ver un ejemplo de cómo se hace, vamos a sacar todas las asíntotas horizontales de la siguiente función racional:

f(x)=\cfrac{x+1}{x-1}

Para determinar las asíntotas horizontales, tenemos que calcular el límite en el menos infinito y en el más infinito de la función:

\displaystyle \lim_{x \to +\infty} \cfrac{x+1}{x-1} = \cfrac{+\infty}{+\infty}= \cfrac{1}{1} = \bm{1}

\displaystyle \lim_{x \to -\infty} \cfrac{x+1}{x-1} = \cfrac{-\infty}{-\infty}= \cfrac{1}{1} = \bm{1}

➤ Ver: cómo resolver la indeterminación infinito entre infinito

Los dos límites al infinito dan 1, por lo tanto, y=1 es la única asíntota horizontal de la función.

A continuación, tienes la función representada gráficamente. Como puedes ver, la función se va acercando mucho a y=1 (tanto en más infinito como en menos infinito), pero nunca lo llega a tocar porque es una asíntota horizontal.

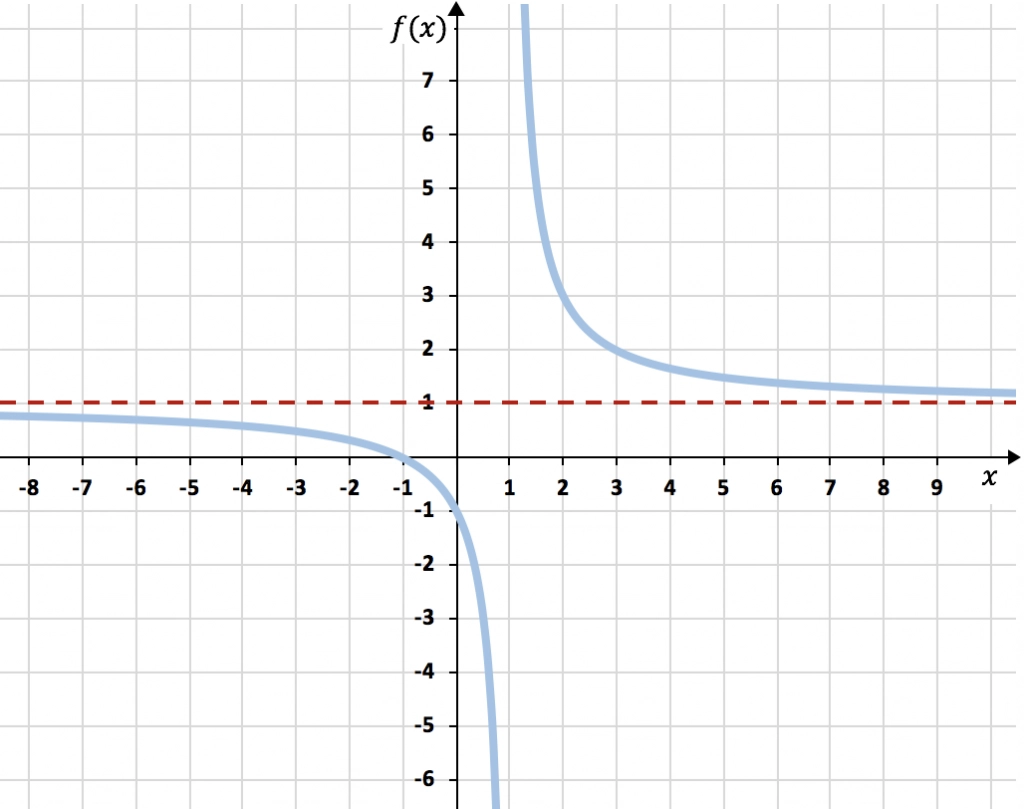
asintota horizontal ejemplo

Nota: en el algunos casos especiales la función corta la asíntota horizontal en uno o más puntos, pero en general la gráfica de una función nunca llega a cruzar sus asíntotas.

Por otro lado, esta función también tiene una asíntota vertical en x=1. Porque, como ves en el gráfica, se acerca mucho a la recta x=1 pero nunca llega a tocar ese valor.

Ejercicios resueltos de asíntotas horizontales

Ejercicio 1

Encuentra la asíntota horizontal, si tiene, de la siguiente función fraccionaria:

\displaystyle f(x)= \frac{4x+3}{2x-1}

Para determinar las asíntotas horizontales de la función racional tenemos que calcular los límites al infinito de la función:

\displaystyle \lim_{x \to +\infty} \frac{4x+3}{2x-1} = \frac{4(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{4}{2} = \bm{2}

\displaystyle \lim_{x \to -\infty} \frac{4x+3}{2x-1} = \frac{4(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{4}{2} = \bm{2}

En este caso el resultado de la forma indeterminada ∞/∞ es la división de los coeficientes de las x de mayor grado, ya que el numerador y el denominador son del mismo orden.

Los límites al más infinito y al menos infinito de la función dan 2, por tanto, y=2 es una asíntota horizontal y es la única que tiene la función.

 

Ejercicio 2

Halla todas las asíntotas horizontales de la siguiente función racional con una raíz:

\displaystyle f(x)= \frac{3x}{\sqrt{x^2+2}}

Para hallar las asíntotas horizontales de la función, primero calculamos el límite al infinito positivo:

\displaystyle \lim_{x \to +\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{+\infty}{+\infty} = \frac{3}{\sqrt{1}} = \bm{3}

Y luego resolvemos el límite de la función en el infinito negativo:

\displaystyle \lim_{x \to -\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{-\infty}{+\infty} = \frac{-3}{\sqrt{1}} = \bm{-3}

➤ Si tienes dudas de cómo se han resuelto los límites al infinito, te recomendamos que le eches un vistazo al enlace de más arriba de cómo resolver la indeterminación infinito entre infinito.

En este caso, hemos obtenido dos valores diferentes de los límites al infinito. De modo que la función tiene dos asíntotas horizontales: y=3 es una asíntota horizontal de la función por la derecha y, por otra parte, y=-3 es una asíntota horizontal de la función por la izquierda.

 

Ejercicio 3

Calcula las asíntotas horizontales de la siguiente función definida a trozos:

\displaystyle f(x)=\left\{ \begin{array}{lcl}\displaystyle\frac{3x-1}{x^2}& \text{si} & x<4\\[4ex]\displaystyle\frac{x^3-2x+5}{2x^3-9} & \text{si} & x\geq 4 \end{array} \right.

Para hacer el cálculo de las asíntotas horizontales de la función no existe ninguna fórmula, sino que debemos calcular los límites al más y al menos infinito.

Entonces, para hallar el límite al menos infinito cogemos la función definida en el primer tramo:

\displaystyle \lim_{x \to -\infty}\frac{3x-1}{x^2}= \frac{-\infty}{+\infty}=\bm{0}

Así que la recta y=0 es una asíntota horizontal por la izquierda de la función.

Y ahora calculamos el límite al más infinito tomando la función definida en el segundo tramo:

\displaystyle \lim_{x \to +\infty}\frac{x^3-2x+5}{2x^3-9}= \frac{+\infty}{+\infty}=\mathbf{\frac{1}{2}}

De manera la recta y=1/2 es una asíntota horizontal por la derecha de la función.

 

4 comentarios en “Asíntota horizontal”

  1. william

    bien ya sabemos como hallar la asíntota teniendo la ecuación de una grafica, pero como hallar la ecuación de la asíntota teniendo la grafica?
    seria de gran ayuda que dieras unos ejemplos o explicación de mi pregunta.

    Responder
    1. Funciones

      Hola William,

      Las asíntotas horizontales siempre tienen una ecuación del tipo y=k, donde k es el número en el que la asíntota corta el eje OY.

      Por ejemplo, si te fijas en la función representada gráficamente en el apartado «Ejemplo de asíntota horizontal», la ecuación de su asíntota horizontal es y=1.

    1. Funciones

      Hola Yosvani,

      Para encontrar la asíntota horizontal de la función que propones tienes que calcular el límite de dicha función al infinito:

      \displaystyle\lim_{x\to +\infty} \frac{1}{x}+3-2=\frac{1}{+\infty}+3-2=0+3-2=1

      \displaystyle\lim_{x\to -\infty} \frac{1}{x}+3-2=\frac{1}{-\infty}+3-2=0+3-2=1

      Ambos límites al infinito dan como resultado 1, por lo tanto, y=1 es la asíntota horizontal de la función.

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *