▷ Integral del coseno

En este post te explicamos cómo resolver la integral del coseno. Así pues, encontrarás cuál es la fórmula de la integral del coseno y, además, podrás ver varios ejemplos resueltos de este tipo de integrales trigonométricas.

Índice

Fórmula de la integral del coseno

La integral del coseno de x es igual al seno de x más la constante de integración.

$\displaystyle\int\text{cos}(x)\ dx=\text{sen}(x)+C$

Cuando en el argumento del coseno de la integral tenemos una función y además el coseno está multiplicado por la derivada de dicha función, la integral es igual al seno de la función más la constante de integración.

$\displaystyle\int\text{cos}(u)\cdot u'\ dx=\text{sen}(u)+C$

En definitiva, la fórmula de la integral del coseno es la siguiente:

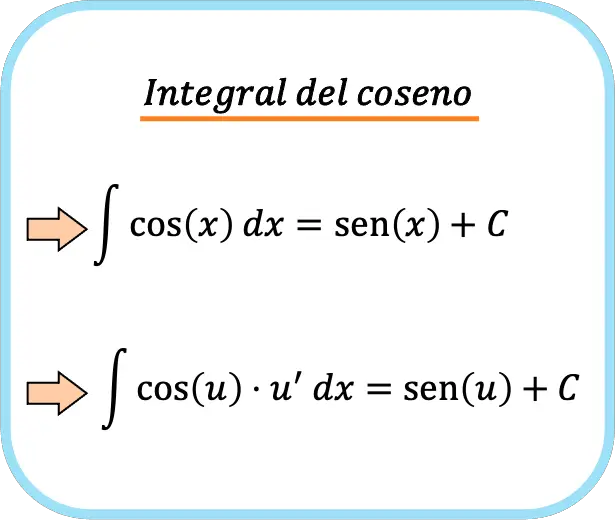
➤ Ver: Derivada del coseno

Ejemplo de la integral del coseno

Para que puedas ver cómo se calcula una integral de la función coseno, a continuación te dejamos un ejemplo en el que se resuelve la integral del coseno de 2x.

$\displaystyle\int\text{cos}(2x)\ dx$

En el argumento del coseno no hay una simple x, sino que tenemos una función. Por lo tanto, para poder resolver esta integral trigonométrica necesitamos que el coseno esté multiplicado por la derivada de la función del argumento. Así pues, debemos multiplicar y dividir por su derivada (2) y luego sacar el denominador fuera de la integral:

$\displaystyle\int\text{cos}(2x)\ dx=\int\frac{2}{2}\cdot\text{cos}(2x)\ dx=\frac{1}{2}\int 2\text{cos}(2x)\ dx$

Ahora que ya tenemos el coseno multiplicado por la derivada de su argumento, podemos aplicar la fórmula de la integral del coseno:

$\displaystyle\int\text{cos}(u)\cdot u'\ dx=\text{sen}(u)+C$

De modo que el resultado de la integral es el siguiente:

$\displaystyle\frac{1}{2}\int 2\text{cos}(2x)\ dx=\frac{1}{2}\cdot \text{sen}(2x)+C=\frac{\text{sen}(2x)}{2}+C$

Ejercicios resueltos de integrales de cosenos

Resuelve las siguientes integrales de funciones seno:

$\text{A) } \displaystyle\int\bigl(5x-\text{cos}(x)\bigr)\ dx$

$\text{B) } \displaystyle\int\text{cos}(4x+9)\ dx$

$\text{C) } \displaystyle\int(x+1)\text{cos}(x^2+2x-4)\ dx$

$\text{D) } \displaystyle\int e^{5x}\text{cos}\left(e^{5x}\right)\ dx$

Ver solución

$\text{A) } \displaystyle\int\bigl(5x-\text{cos}(x)\bigr)\ dx =\int 5x\ dx - \int \text{cos}(x) \ dx=\cfrac{5x^2}{2}-\text{sen}(x)+C$

$\text{B) } \displaystyle\int\text{cos}(4x+9)\ dx =\frac{1}{4}\int 4\cdot \text{cos}(4x+9)\ dx =\frac{\text{sen}(4x+9)}{4}+C$

$\begin{aligned}\text{C) }& \displaystyle\int(x+1)\text{cos}(x^2+2x-4)\ dx\longrightarrow \left\{\begin{array}{c}u=x^2+2x-4\\[2ex] du=(2x+2)dx=2(x+1)dx\end{array}\right\}\\[2ex]&=\int \frac{(x+1)\text{cos}(u)}{2(x+1)}\ du=\\[2ex]&=\frac{1}{2}\int\text{cos}(u)\ du=\frac{\text{sen}(u)}{2}+C=\\[2ex]&=\frac{\text{sen}(x^2+2x-4)}{2}+C \end{aligned}$

$\text{D) } \displaystyle\int e^{5x}\text{cos}\left(e^{5x}\right)\ dx =\frac{1}{5}\int 5e^{5x}\text{cos}\left(e^{5x}\right)\ dx=\frac{\text{sen}\left(e^{5x}\right)}{5}+C$

➤ Ver: Integral del seno

Integral de coseno al cuadrado

La integral de coseno al cuadrado de x es igual a x partido por dos más el seno de 2x partido por cuatro más la constante de integración.

$\displaystyle\int\text{cos}^2(x) \ dx=\frac{x}{2}+\frac{\text{sen}(2x)}{4}+C$

Puede que te cueste ver cómo se llega a este resultado, pues la integral del coseno al cuadrado es más difícil de resolver que la integral del coseno. Como seguramente te interesa, te dejo el siguiente enlace en el que se demuestra la fórmula de la integral del coseno al cuadrado:

➤ Ver: Demostración de la fórmula de la integral de coseno al cuadrado

Fórmula de la integral del coseno

Ejemplo de la integral del coseno

Ejercicios resueltos de integrales de cosenos

Integral de coseno al cuadrado

Deja un comentario Cancelar respuesta