▷ Función Coseno: gráfica, características, fórmula...

En esta página encontrarás todo sobre la función coseno: qué es, cuál es su fórmula, cómo representarla en una gráfica, las características de la función, amplitud, periodo, etc. Además, podrás ver diferentes ejemplos de funciones coseno para entender el concepto totalmente. Incluso se explica el teorema del coseno y las relaciones que tiene la función coseno con las otras razones trigonométricas.

Índice

Fórmula de la función coseno

La función coseno de un ángulo α es una función trigonométrica cuya fórmula se define como la razón entre el cateto contiguo (o adyacente) y la hipotenusa de un triángulo rectángulo (triángulo con un ángulo recto).

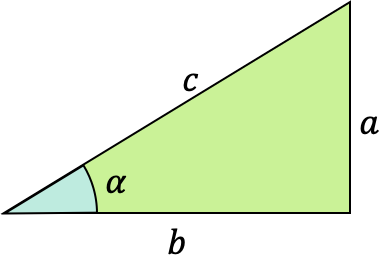
A este tipo de función matemática también se le llama cosinusoide, cosenoide o función cosenoidal.

La función coseno es una de las tres razones trigonométricas más conocidas, junto con el seno y la tangente de un ángulo.

Valores característicos de la función coseno

Hay algunos ángulos determinados que se repiten frecuentemente y, por lo tanto, es conveniente saber el valor de la función coseno en estos ángulos:

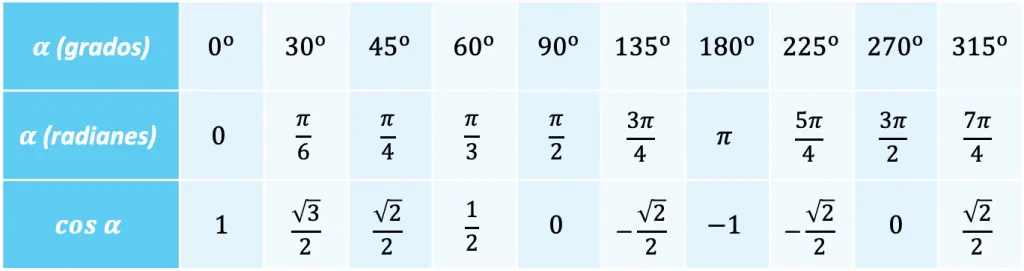
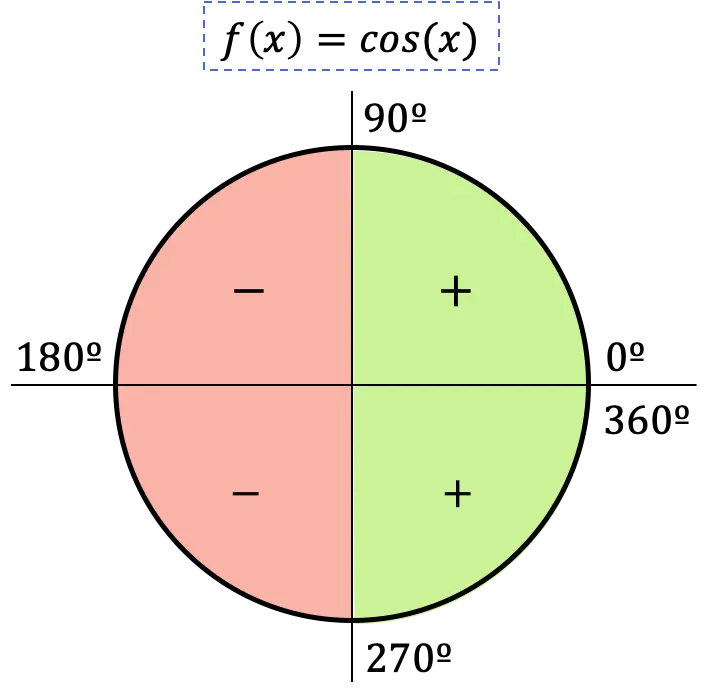
De modo que el signo de la función coseno depende del cuadrante en el que se encuentre el ángulo: si el ángulo está dentro del primero o cuarto cuadrantes el coseno será positivo, por contra, si el ángulo cae en el segundo o tercer cuadrante el coseno será negativo.

Representación gráfica de la función coseno

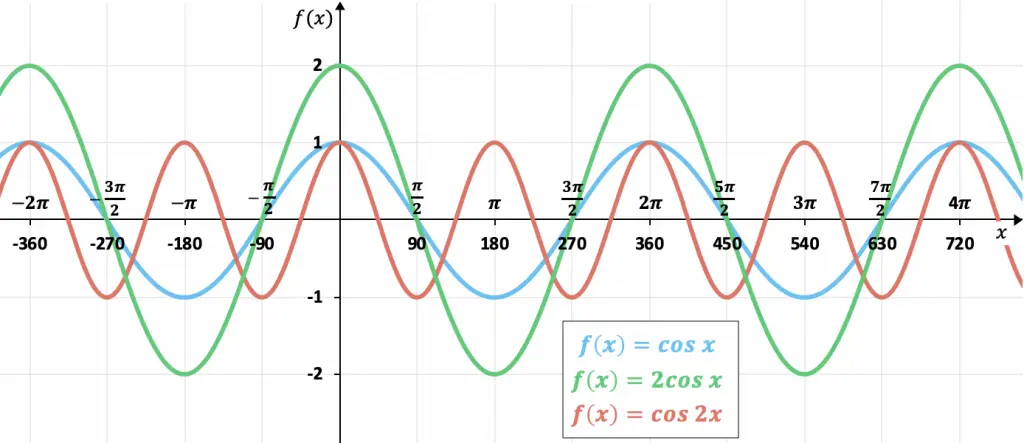
Con la tabla de valores que hemos visto en el apartado anterior podemos graficar la función coseno. Y al representar la función coseno gráficamente se obtiene:

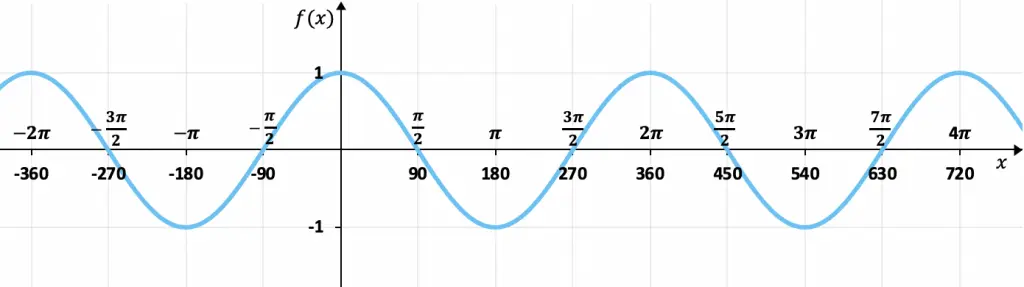
Como puedes ver en la gráfica, los valores de las imágenes de la función coseno siempre están entre +1 y -1, es decir, está acotada superiormente por +1 e inferiormente por -1. Además, los valores se van repitiendo cada 360 grados (2π radianes), por lo que se trata de una función periódica cuyo periodo es 360º.

Por otro lado, en este gráfico se aprecia perfectamente que la función coseno es par, porque sus elementos opuestos tienen la misma imagen, o dicho de otra forma, es simétrica respecto el eje de las ordenadas (eje Y). Por ejemplo, el coseno de 90º es 0 y el de -90º es 0.

Propiedades de la función coseno

La función coseno tiene las siguientes características:

El dominio de la función coseno son todos los números reales ya que, como se ve en la gráfica, la función existe por cualquier valor de la variable independiente x.

$\text{Dom } f = \mathbb{R}$

El recorrido o rango de la función coseno va desde el 1 negativo hasta el 1 positivo (ambos incluidos).

$\text{Im } f= [-1,1]$

Se trata de una función continua y par de periodicidad 2π.

$\displaystyle \text{cos }x = \text{cos}(-x)$

Este tipo de función trigonométrica tiene un único punto de corte con el eje OY en el punto (0,1).

$(0,1)$

En cambio, intercepta periódicamente con el eje de las abscisas (eje X) en las coordenadas múltiples impares de pi medios.

$\displaystyle \left(\frac{\pi}{2}+k\pi ,0\right) \qquad k \in \mathbb{Z}$

El máximo de la función coseno se produce cuando:

$x = 2\pi k \qquad k \in \mathbb{Z}$

Y al contrario, el mínimo de la función coseno tiene lugar en:

$x = \pi(2k +1 ) \qquad k \in \mathbb{Z}$

La derivada de la función coseno es el seno cambiado de signo:

$f(x)=\text{cos } x \ \longrightarrow \ f'(x)= -\text{sen } x$

Por último, la integral de la función coseno es el seno:

$\displaystyle \int \text{cos } x \ dx= \text{sen } x + C$

Periodo y amplitud de la función coseno

Como hemos visto en su gráfica la función coseno es una función periódica, es decir, sus valores se van repitiendo según una frecuencia. Además, los valores máximos y mínimos entre los que oscila depende de su amplitud. De manera que dos rasgos importantes que determinan la función coseno son su periodo y su amplitud:

$\displaystyle f(x)= A\text{cos}(wx)$

El periodo de la función coseno es la distancia entre dos puntos en los que se repite la gráfica, y se calcula con la siguiente fórmula:

$\displaystyle \text{Periodo}=T=\cfrac{2\pi}{w}$

La amplitud de la función coseno es equivalente al coeficiente de delante del término coseno.

$\displaystyle \text{Amplitud}=A$

A continuación puedes ver un gráfico donde se aprecian los efectos de cambiar el periodo o la amplitud:

En la función representada de color verde podemos ver que al duplicar la amplitud la función va desde +2 hasta -2, en vez de +1 a -1. Por otro lado, en la función representada de color rojo se puede apreciar como esta va el doble de rápido que la función coseno «canónica», ya que se ha reducido a la mitad su periodo.

Teorema del coseno

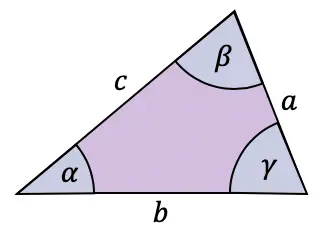
Aunque normalmente la fórmula del coseno se utiliza en triángulos rectángulos, también existe un teorema que se puede aplicar en cualquier tipo de triángulo: el teorema del coseno o de los cosenos.

El teorema del coseno relaciona los lados y los ángulos de un triángulo cualquiera de la siguiente manera:

$a^2=b^2+c^2-2\cdot b \cdot c\cdot \text{cos }\alpha$

$b^2=a^2+c^2-2\cdot a \cdot c\cdot \text{cos }\beta$

$c^2=a^2+b^2-2\cdot a \cdot b\cdot \text{cos }\gamma$

Relaciones de la función coseno con otras razones trigonométricas

A continuación tienes las relaciones del coseno con las razones trigonométricas más importantes de la trigonometría.

Relación con el seno

La gráfica de la función seno es equivalente a la curva del coseno pero desplazada $\displaystyle \frac{\pi}{2}$ a la derecha, por lo que las dos funciones se pueden relacionar mediante la siguiente expresión:

$\displaystyle \text{cos }\alpha = \text{sen}\left(\alpha + \frac{\pi}{2} \right)$

También se pueden relacionar el seno y el coseno con la identidad fundamental trigonométrica:

$\displaystyle \text{sen}^2\alpha + \text{cos}^2\alpha=1$

Relación con la tangente

Aunque es complejo de demostrar, se puede expresar el coseno únicamente en función de la tangente:

$\displaystyle \text{cos }\alpha = \pm \cfrac{1}{\sqrt{1+\text{tg}^2\alpha \vphantom{\bigl( }}}$

Relación con la secante

El coseno y la secante son inversos multiplicativos:

$\displaystyle \text{cos }\alpha = \cfrac{1}{\text{sec }\alpha}$

Relación con la cosecante

Se puede despejar el coseno para que solo dependa de la cosecante:

$\displaystyle \text{cos }\alpha =\pm \cfrac{\sqrt{\text{csc}^2\alpha -1 } }{\text{csc }\alpha}$

Relación con la cotangente

El coseno y la cotangente de un ángulo se relacionan mediante la siguiente ecuación:

$\displaystyle \text{cos }\alpha =\pm \cfrac{\text{cot }\alpha}{\sqrt{1+\text{cot}^2\alpha \vphantom{\bigl( }}}$

Función coseno