Función tangente hiperbólica

En esta página encontrarás todo sobre la tangente hiperbólica: cuál es su fórmula, su representación gráfica, todas sus características,…

Fórmula de la tangente hiperbólica

La función tangente hiperbólica es una de las principales funciones hiperbólicas y se representa con el símbolo tanh(x). Matemáticamente, la tangente hiperbólica es igual al seno hiperbólico dividido entre el coseno hiperbólico.

\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}

A partir de la fórmula del seno hiperbólico y la fórmula del coseno hiperbólico podemos llegar a la siguiente expresión:

\text{tanh}(x)=\cfrac{e^x-e^{-x}}{e^x+e^{-x}}

Por lo tanto, la función tangente hiperbólica está relacionada con la función exponencial. En el siguiente enlace puedes ver todas las características de estos tipos de funciones:

➤ Ver: características de las funciones exponenciales

Representación gráfica de la tangente hiperbólica

A partir de su fórmula, podemos representar gráficamente la función tangente hiperbólica:

tangente hiperbolica

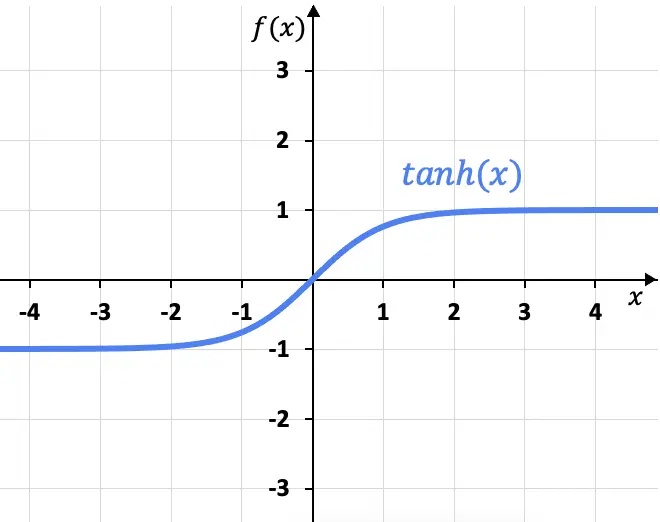
Como puedes ver en el gráfico, la función tangente hiperbólica tiene dos asíntotas horizontales en x=+1 y x=-1, ya que el límite de la función cuando x tiende a más infinito da como resultado x=+1, y el límite al menos infinito da x=-1.

Por otra parte, la gráfica de la tangente hiperbólica no se parece en nada a la gráfica de la tangente (función trigonométrica), que es una función periódica. Puedes ver la representación gráfica de la tangente y en qué se diferencia respecto a la tangente hiperbólica en el siguiente enlace:

➤ Ver: representación gráfica de la función tangente

Características de la tangente hiperbólica

La función tangente hiperbólica posee las siguientes propiedades:

  • El dominio de la función tangente hiperbólica son todos los números reales.

\text{Dom } f = \mathbb{R}

  • Por contra, el recorrido o rango de la función tangente hiperbólica se limita a los valores comprendidos entre -1 y +1 (no incluidos).

\text{Im } f= (-1,1)

  • La tangente hiperbólica es una función continua, biyectiva e impar (simétrica respecto el origen de coordenadas).

\displaystyle \text{tanh}(-x) =- \text{tanh}(x)

  • La función corta el eje X y el eje Y en el origen de coordenadas.

(0,0)

  • Los límites al más/menos infinito de la función tangente hiperbólica dan como resultado +1/-1. Por lo tanto, la función tiene una asíntota horizontal en x=+1, y otra asíntota horizontal en x=-1.

\displaystyle\lim_{x\to+\infty}\text{tanh}(x)=+1

\displaystyle\lim_{x\to-\infty}\text{tanh}(x)=-1

  • La tangente hiperbólica es estrictamente creciente en todo su dominio, así que no tiene ningún extremo relativo (ni máximo ni mínimo).
  • Sin embargo, la función pasa de ser convexa a ser cóncava en el punto x=0, de manera que x=0 es un punto de inflexión de la función.
  • La inversa de la función tangente hiperbólica se llama argumento tangente hiperbólica (o arco tangente hiperbólica) y su fórmula es la siguiente:

\displaystyle\text{tanh}^{-1}(x)=\text{arg tanh}(x)=\cfrac{1}{2}\ln\left(\frac{1+x}{1-x}\right)

  • La derivada de la función tangente hiperbólica es 1 partido por el cuadrado del coseno hiperbólico:

f(x)=\text{tanh}(x) \ \longrightarrow \ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=1-\text{tanh}^2(x)

  • La integral de la función tangente hiperbólica es el logaritmo neperiano del coseno hiperbólico:

\displaystyle\int\text{tanh}(x) \ dx= \ln\Bigl(\text{cosh}(x)\Bigr)+C

  • La tangente hiperbólica de la suma de dos números distintos se puede calcular aplicando la siguiente ecuación:

\text{tanh}(x+y)=\cfrac{\text{tanh}(x)+\text{tanh}(y)}{1+\text{tanh}(x)\cdot \text{tanh}(y)}

  • El polinomio o serie de Taylor de la tangente hiperbólica tiene como radio de convergencia \left|x\right|<\cfrac{\pi}{2} y corresponde a la siguiente expresión:

\displaystyle\text{tanh}(x)=x-\frac{x^3}{3}+\frac{2x^5}{15}-\frac{17x^7}{315}+\cdots =\sum_{n=1}^\infty\frac{2^{2n}(2^{2n}-1)B_{2n} x^{2n-1}}{(2n)!}

Donde B_n es el número de Bernoulli.

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *