▷ Función seno hiperbólico: fórmula, gráfica, características,...

En este post encontrarás todo sobre el seno hiperbólico: cuál es su fórmula, su representación gráfica, todas sus características, las relaciones con otras funciones,…

Índice

Fórmula del seno hiperbólico

La función seno hiperbólico es una de las principales funciones hiperbólicas y se representa con el símbolo senh(x) o sinh(x). El seno hiperbólico es igual a e^x menos e^-x dividido entre 2.

Por lo tanto, la fórmula del seno hiperbólico es la siguiente:

$\displaystyle\text{senh}(x)=\cfrac{e^{x}-e^{-x}}{2}$

De modo que el seno hiperbólico está relacionado con la función exponencial.

➤ Ver: características de la función exponencial

Representación gráfica del seno hiperbólico

Utilizando la fórmula que hemos visto en el apartado anterior, podemos hacer una tabla de valores del seno hiperbólico y representar la función gráficamente:

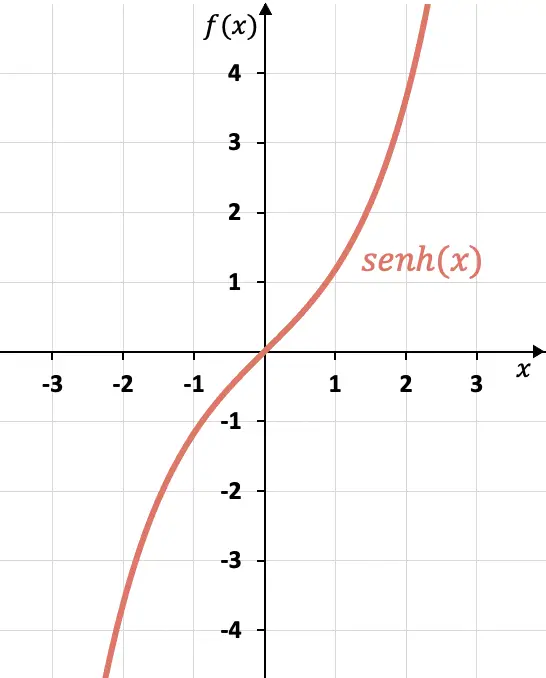
En este gráfico se aprecia que el seno hiperbólico es una función impar, porque las x opuestas tienen imágenes opuestas, o dicho con otras palabras, la gráfica del seno hiperbólico es simétrica respecto el origen de coordenadas (0,0).

Como puedes ver, la gráfica del seno hiperbólico es muy diferente a la del seno, que es una función periódica. Puedes ver la representación gráfica del seno y todas las diferencias con el seno hiperbólico en el siguiente enlace:

➤ Ver: Representación gráfica de la función seno

Características del seno hiperbólico

El seno hiperbólico tiene las siguientes propiedades:

El dominio de la función seno hiperbólico son todos los números reales:

$\text{Dom } f = \mathbb{R}$

El recorrido o rango de la función seno hiperbólico también son todos los números reales.

$\text{Im } f= \mathbb{R}$

El seno hiperbólico es una función continua e impar.

$\displaystyle \text{senh}(-x) =- \text{senh}(x)$

Intercepta el eje X y el eje Y en el mismo punto de corte, el origen de coordenadas:

$(0,0)$

El límite de la función seno hiperbólico cuando x tiende al más/menos infinito es igual a más/menos infinito:

$\displaystyle\lim_{x\to+\infty}\text{senh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{senh}(x)=-\infty$

El seno hiperbólico es estrictamente creciente en todo el dominio, por lo que no tiene ni máximos ni mínimos.

Sin embargo, sí que cambia su curvatura en el punto x=0, por lo que es un punto de inflexión de la función. Para valores menores de x=0 se trata de una función cóncava, en cambio, para valores mayores de x=0 es una función convexa.

La derivada de la función seno hiperbólico es el coseno hiperbólico:

$f(x)=\text{senh}(x) \ \longrightarrow \ f'(x)=\text{cosh}(x)$

Del mismo modo, la integral de la función seno hiperbólico es el coseno hiperbólico:

$\displaystyle \int \text{senh}(x) \ dx= \text{cosh}(x) + C$

La serie de Taylor de la función seno hiperbólico es equivalente a la siguiente expresión:

$\displaystyle\text{senh}(x)=x+\cfrac{x^3}{3!}+\cfrac{x^5}{5!}+\cfrac{x^7}{7!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n+1}}{(2n+1)!}$

La transformada de Laplace de la función seno hiperbólico es la siguiente:

$\mathcal{L}\bigl[\text{senh}(at)\bigr]=\cfrac{a}{s^2-a^2}$

Relaciones matemáticas del seno hiperbólico

El seno hiperbólico está relacionado con las otras funciones hiperbólicas mediante las siguientes ecuaciones:

La ecuación fundamental relaciona el seno hiperbólico con el coseno hiperbólico:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

Por tanto, las funciones hiperbólicas seno y coseno están relacionadas mediante la ecuación de la hipérbola, que es x²-y²=1. A diferencia de las funciones trigonométricas seno y coseno que están vinculadas a través de la ecuación de la circunferencia (x²+y²=1).

Las funciones hiperbólicas del seno, coseno y tangente se pueden relacionar mediante la siguiente ecuación:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

Por otro lado, el seno hiperbólico de la suma o resta de dos números distintos se puede calcular con las siguientes fórmulas:

$\text{senh}(x+y)=\text{senh}(x)\text{cosh}(y)+\text{senh}(y)\text{cosh}(x)$

$\text{senh}(x-y)=\text{senh}(x)\text{cosh}(y)-\text{senh}(y)\text{cosh}(x)$

El seno hiperbólico del doble de un número se puede determinar aplicando la siguiente relación matemática:

$\text{senh}(2x)=2\text{senh}(x)\text{cosh}(x)$

La suma o resta de dos senos hiperbólicos se pueden hallar utilizando las siguientes fórmulas:

$\displaystyle\text{senh}(x)+\text{senh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{senh}(x)-\text{senh}(y)=2\text{senh}\left(\frac{x-y}{2}\right)\text{cosh}\left(\frac{x+y}{2}\right)$

Por último, el cuadrado del seno hiperbólico se puede calcular aplicando la siguiente fórmula:

$\text{senh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)-1\Bigr)$

Fórmula del seno hiperbólico

Representación gráfica del seno hiperbólico

Características del seno hiperbólico

Relaciones matemáticas del seno hiperbólico

Deja un comentario Cancelar respuesta