Función coseno hiperbólico

Aquí encontrarás todo sobre la función coseno hiperbólico: cuál es su fórmula, su representación gráfica, sus características, las relaciones matemáticas con otras funciones,…

Fórmula del coseno hiperbólico

La función coseno hiperbólico es una de las principales funciones hiperbólicas y se representa con el símbolo cosh(x). El coseno hiperbólico es igual a la suma de ex más e-x dividido entre 2.

Por lo tanto, la fórmula del coseno hiperbólico es la siguiente:

\displaystyle\text{cosh}(x)=\cfrac{e^{x}+e^{-x}}{2}

Así que el coseno hiperbólico está matemáticamente relacionado con la función exponencial. En el siguiente enlace puedes ver las propiedades de este tipo de función:

➤ Ver: propiedades de la función exponencial

Representación gráfica del coseno hiperbólico

La representación gráfica de la función coseno hiperbólico tiene forma de función cuadrática (o parábola):

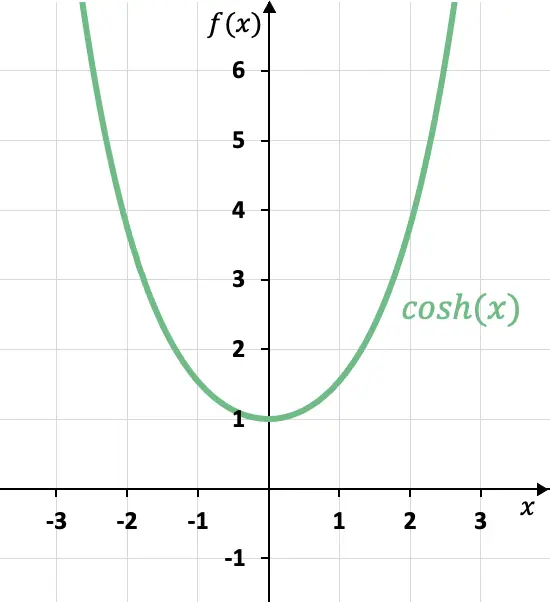
coseno hiperbolico

➤ Ver: cómo graficar una función cuadrática.

En este gráfico podemos ver claramente que el coseno hiperbólico es una función par, ya que es simétrica respecto el eje de las ordenadas.

Por otro lado, la gráfica del coseno hiperbólico es muy diferente a la del coseno (función trigonométrica), que es una función periódica. Puedes ver la representación gráfica del coseno y todas las diferencias con el coseno hiperbólico en el siguiente enlace:

➤ Ver: representación gráfica de la función coseno

Características del coseno hiperbólico

El coseno hiperbólico cumple con las siguientes propiedades:

  • El dominio de la función coseno hiperbólico son todos los números reales:

\text{Dom } f = \mathbb{R}

  • En cambio, el recorrido (o rango) de la función coseno hiperbólico son 1 y todos los números mayores que 1:

\text{Im } f= [1,+\infty)

  • El coseno hiperbólico es una función continua y par.

\displaystyle \text{cosh}(-x)=\text{cosh}(x)

  • La función corta el eje Y en el punto x=0.

(0,1)

  • Por contra, la función no tiene punto de corte con el eje X.
  • Ambos límites al infinito (positivo y negativo) de la función coseno hiperbólico dan como resultado más infinito.

\displaystyle\lim_{x\to+\infty}\text{cosh}(x)=+\infty

\displaystyle\lim_{x\to-\infty}\text{cosh}(x)=+\infty

  • El coseno hiperbólico decrece hasta x=0 y a partir de ese punto crece indefinidamente, por lo que la función tiene un mínimo en x=0.

(0,1)

  • La función es convexa en todo su dominio, así que no tiene ningún punto de inflexión.
  • La derivada de la función coseno hiperbólico es el seno hiperbólico:

f(x)=\text{cosh}(x) \ \longrightarrow \ f'(x)=\text{senh}(x)

  • La integral de la función coseno hiperbólico es el seno hiperbólico:

\displaystyle \int \text{cosh}(x) \ dx= \text{senh}(x) + C

  • El polinomio de Taylor (o serie de Maclaurin) de la función coseno hiperbólico es el siguiente:

\displaystyle\text{cosh}(x)=1+\cfrac{x^2}{2!}+\cfrac{x^4}{4!}+\cfrac{x^6}{6!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n}}{(2n)!}

  • La transformada de Laplace de la función coseno hiperbólico es la siguiente:

\mathcal{L}\bigl[\text{cosh}(at)\bigr]=\cfrac{s}{s^2-a^2}

Relaciones matemáticas del coseno hiperbólico

A continuación, vamos a ver cómo se puede calcular el coseno hiperbólico a partir de otras funciones hiperbólicas, ya que todas ellas están relacionadas matemáticamente.

La ecuación fundamental relaciona el coseno hiperbólico con el seno hiperbólico:

\text{cosh}^2(x)-\text{senh}^2(x)=1

➤ Ver: seno hiperbólico

Las tres funciones hiperbólicas principales (el seno, el coseno y la tangente hiperbólicos) se pueden relacionar mediante la siguiente ecuación:

\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}

Por otro lado, el coseno hiperbólico de la suma (o resta) de dos números distintos se puede determinar mediante las siguientes fórmulas:

\text{cosh}(x+y)=\text{cosh}(x)\text{cosh}(y)+\text{senh}(y)\text{senh}(x)

\text{cosh}(x-y)=\text{cosh}(x)\text{cosh}(y)-\text{senh}(y)\text{senh}(x)

El coseno hiperbólico del doble de un número es igual a la suma de los cuadrados del coseno hiperbólico y del seno hiperbólico de dicho número:

\text{cosh}(2x)=\text{cosh}^2(x)+\text{senh}^2(x)

La suma o la resta de dos cosenos hiperbólicos se pueden calcular aplicando las siguientes fórmulas:

\displaystyle\text{cosh}(x)+\text{cosh}(y)=2\text{cosh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)

\displaystyle\text{cosh}(x)-\text{cosh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{senh}\left(\frac{x-y}{2}\right)

Finalmente, el cuadrado del coseno hiperbólico se puede calcular con la siguiente fórmula:

\text{cosh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)+1\Bigr)

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *