▷ Área entre dos funciones

En este artículo te explicamos cómo se calcula el área entre dos funciones. De modo que encontrarás cuál es la fórmula que sirve para hallar el área entre dos funciones y, además, un ejercicio resuelto paso a paso para acabar de entender el concepto.

Índice

Cómo calcular el área entre dos funciones

El área entre dos funciones es igual al área bajo la función cuya gráfica está por encima menos el área bajo la otra función.

Así pues, para calcular el área entre dos funciones se debe resolver la integral definida de la diferencia de las funciones en el intervalo formado por los puntos de corte de las dos funciones.

Por lo tanto, la fórmula para calcular el área entre dos funciones es la siguiente:

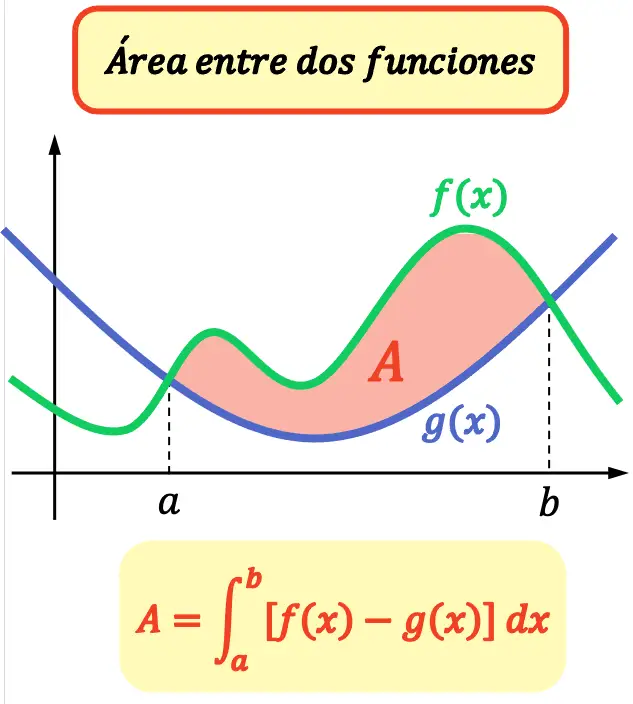
Donde:

$\displaystyle A$ es el área entre las dos funciones.
$\displaystyle a$ es el punto de corte menor entre ambas funciones.
$\displaystyle b$ es el punto de corte mayor entre ambas funciones.
$\displaystyle f(x)$ es la función cuya gráfica queda por encima.
$\displaystyle g(x)$ es la función cuya gráfica queda por debajo.
$\displaystyle dx$ es el diferencial de x, que indica la variable a integrar.

➤ Ver: Área bajo una curva

Ejemplo del cálculo del área entre dos funciones

Para que puedas ver cómo se halla el área entre dos funciones, a continuación te dejamos un ejemplo resuelto.

Calcula el área comprendida entre las gráficas de las siguientes dos funciones:

$\begin{array}{c}y=x^2+2x+1\\[2ex]y=x+1\end{array}$

La primero que debemos hacer es determinar las coordenadas X de los puntos de corte entre las dos funciones. Para ello, resolvemos el sistema de ecuaciones formado por las dos funciones igualando sus expresiones:

$x^2+2x+1=x+1$

$x^2+2x+1-x-1=0$

$x^2+x=0$

$\displaystyle x(x+1)=0 \ \begin{cases}x=0\\[2ex]x+1=0 \ \longrightarrow \ x=-1\end{cases}$

➤ Ver: Puntos de corte de una función

Las dos funciones se cortan entre x=-1 y x=0, así que el área que queremos determinar se encuentra en el intervalo [-1,0].

En el intervalo [-1,0] la gráfica de la función y=x+1 está por encima de la gráfica de la otra función, por lo tanto, la integral definida que debemos resolver para sacar el área entre las dos funciones es la siguiente:

$\displaystyle\int_{-1}^0\left[x+1-\left(x^2+2x+1\right)\right] dx$

$\displaystyle\int_{-1}^0\left[x+1-x^2-2x-1\right] dx$

$\displaystyle\int_{-1}^0\left[-x^2-x\right] dx$

Así pues, resolvemos la integral definida utilizando la regla de Barrow:

$\begin{aligned}&\displaystyle\int_{-1}^0\left[-x^2-x\right] dx=\left[-\frac{x^3}{3}-\frac{x^2}{2}\right]_{-1}^0=\\[2ex]&=-\frac{0^3}{3}-\frac{0^2}{2}-\left(-\frac{(-1)^3}{3}-\frac{(-1)^2}{2}\right)=\\[2ex]&=-\frac{1}{3}+\frac{1}{2}=\frac{1}{6}\end{aligned}$

➤ Ver: Regla de Barrow

Cómo calcular el área entre dos funciones

Ejemplo del cálculo del área entre dos funciones

Deja un comentario Cancelar respuesta