En esta página se explica qué son los puntos de corte (o intersección) de una función con los ejes cartesianos y cómo calcularlos. Además, encontrarás varios ejemplos para entender bien cómo se encuentran e incluso podrás practicar con ejercicios resueltos paso a paso.
Índice
¿Qué son los puntos de corte (o intersección) de una función con los ejes?
Antes de ver cómo se calculan, vamos a recordar qué son los puntos de corte de una función con los ejes.
Los puntos de corte o intersección con los ejes son los puntos donde la representación de una función corta con los ejes de coordenadas, es decir, los puntos de la gráfica que están sobre el eje X y sobre el eje Y.
Por ejemplo, la parábola del siguiente gráfico corta con el eje Y en el punto (0,3) e interseca con el eje X en los puntos (-1,0) y (3,0).
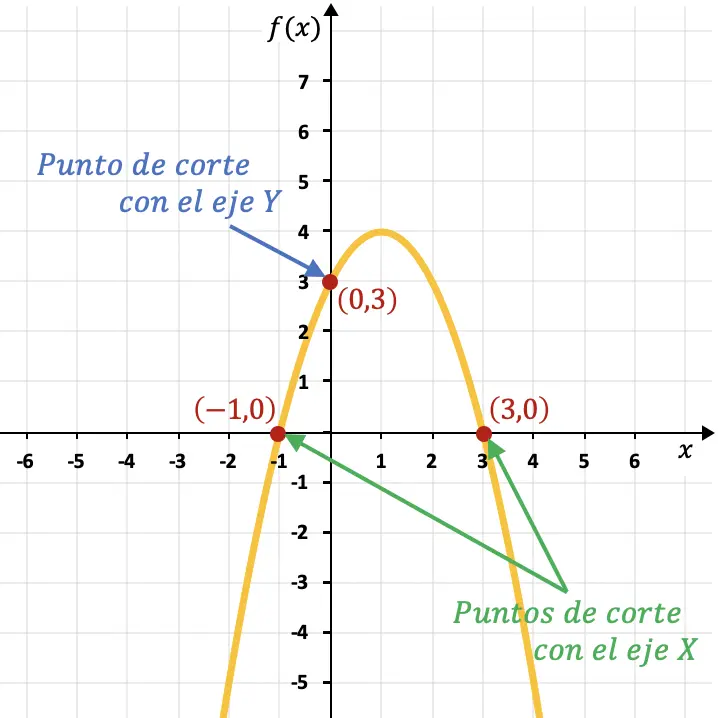
Punto de corte de una función con el eje X
La segunda coordenada de los puntos de intersección de una función con el eje X siempre será 0, por tanto:
Los puntos de corte de cualquier función con el eje de abscisas OX son de la forma 
, y se pueden calcular resolviendo la siguiente ecuación:
En alguna ocasión puede que al resolver esta ecuación obtengamos dos (o más) soluciones, esto significa que la función corta con el eje X dos (o más) veces. Por contra, si la ecuación no tiene ninguna solución implica que la función no corta con el eje X.
Punto de corte de una función con el eje Y
La primera coordenada de los puntos de intersección de una función con el eje Y siempre será 0, por tanto:
El punto de corte de cualquier función con el eje de ordenadas OY es de la forma 
, y se puede hallar calculando la imagen de la función en x=0:
A diferencia de los puntos de corte con el eje X, como máximo solo puede haber un punto de corte con el eje Y.
Ejemplo de cómo calcular los puntos de corte de una función con los ejes
Para que no te quede ninguna duda, a continuación vamos a ver un ejemplo de cómo encontrar los puntos de corte de una función con los ejes cartesianos:
- Halla numéricamente los puntos de corte de la siguiente función:
Primero calcularemos el punto de corte de la función con el eje de las abscisas. El punto de corte con el eje X siempre tendrá la segunda componente igual a 0, es decir será del tipo . Porque f(x) siempre vale 0 en el eje OX. Entonces, para hallar la otra componente del punto tenemos que resolver la ecuación 
De manera que el punto de corte con el eje X es:
Ahora vamos a encontrar el punto de corte con el eje de las ordenadas. El punto de corte con el eje Y siempre tendrá la primera componente igual a 0, es decir el punto será del tipo . Ya que la variable independiente x siempre se anula en el eje Y. Entonces, para hallar la otra coordenada del punto debemos calcular 
De modo que el punto de corte con el eje Y es:
A continuación tienes la función del ejemplo representada gráficamente, puedes ver que los puntos de corte encontrados coinciden con los de la gráfica:
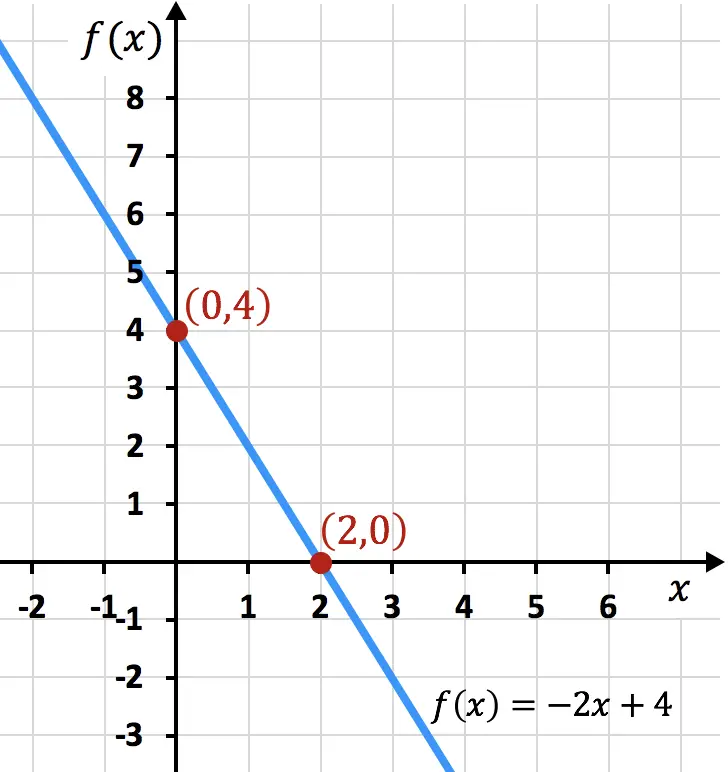
Ejercicios resueltos de puntos de corte de una función con los ejes
Ejercicio 1
Determina los puntos de corte con los ejes de coordenadas de la siguiente función:
Punto de corte con el eje X
Para encontrar el punto de corte de la función con el eje X debemos resolver
De forma que el punto de corte de la función con el eje X es:
Punto de corte con el eje Y
Para hallar el punto de corte con el eje Y debemos calcular
Por lo tanto, el punto de corte de la función con el eje Y es:
Ejercicio 2
Encuentra los puntos de corte con los ejes cartesianos de la siguiente función afín:
Punto de corte con el eje X
Para hallar el punto de corte de la función con el eje OX debemos igualar la función a cero y resolver la ecuación resultante:
De manera que el punto de corte de la función con el eje de las abscisas es:
Punto de corte con el eje Y
Para encontrar el punto de corte con el eje OY debemos calcular
Por lo tanto, el punto de corte de la función con el eje de las ordenadas es:
Ejercicio 3
Calcula los puntos de corte con los ejes de la siguiente función cuadrática:
Punto de corte con el eje X
Para encontrar el punto de corte de la función con el eje X debemos resolver
En este caso tenemos que resolver una ecuación de segundo grado, así que aplicamos la fórmula:
![\displaystyle x=\cfrac{ -(-3) \pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot 1} = \cfrac{3 \pm 1}{2} = \begin{cases} 2 \\[2ex] 1 \end{cases}](https://www.funciones.xyz/wp-content/ql-cache/quicklatex.com-23cd8e87a138bc29cad0997fed740fea_l3.svg "Rendered by QuickLaTeX.com")
Hemos obtenidos dos soluciones de la ecuación cuadrática, por lo que la función corta con el eje X en dos puntos:
Punto de corte con el eje Y
Por otro lado, para determinar el punto de corte con el eje Y hay que calcular
Por lo tanto, el único punto de corte de la función con el eje Y es:
Ejercicio 4
Halla los puntos de corte con los ejes del plano cartesiano de la siguiente función racional:
Punto de corte con el eje X
Para encontrar el punto de corte de la función con el eje X debemos resolver
5 no es equivalente a 0, por tanto, la ecuación no tiene solución y, en consecuencia, no existe ningún punto de intersección entre la función y el eje X.
Punto de corte con el eje Y
Para hallar el punto de corte con el eje Y debemos calcular
Cualquier número dividido entre cero es una indeterminación que da como resultado infinito. Por lo tanto, la función tampoco pasa por encima del eje Y en ningún punto.
En definitiva, la función del ejercicio no tiene ningún punto de corte con los ejes, es decir, su gráfica no pasa ni por el eje X ni por el eje Y en ningún momento.
Ejercicio 5
Calcula los puntos de corte con los ejes de la siguiente función de tercer grado:
Punto de corte con el eje X
Para encontrar el punto de corte de la función con el eje X debemos resolver
Los dos términos de la ecuación tienen una x, con lo que podemos extraer factor común:
Para que la igualdad anterior se cumpla, uno de los factores tiene que dar 0. Por tanto, igualamos cada factor a cero para obtener todas las soluciones posibles:
![\displaystyle x(x^2-9)=0 \ \longrightarrow \begin{cases} \bm{x = 0} \\[2ex] x^2-9 = 0\ \longrightarrow \ x^2=9 \ \longrightarrow \ \bm{x=\pm 3} \end{cases}](https://www.funciones.xyz/wp-content/ql-cache/quicklatex.com-a10fa2c70f1c1d096dd9dc09e9630d21_l3.svg "Rendered by QuickLaTeX.com")
De forma que hemos obtenido tres soluciones de la ecuación de tercer grado, por lo que la función corta con el eje X en 3 puntos:
Punto de corte con el eje Y
Para calcular el punto de corte con el eje Y hay que calcular
Por lo tanto, el único punto de corte de la función con el eje Y es el origen de coordenadas (0,0):
Fíjate que este punto ya lo habíamos encontrado en el cálculo del punto de corte con el eje X, eso es debido a que la función corta en este punto con los dos ejes a la vez.
Hola!
Quiero decirles que muchas gracias por toda la información tan completa que tienen en su sitio web, me ha servido de mucho para realizar mi temario de matemáticas.
¡Gracias por tu comentario Ana!❤