▷ Integral de una raíz (fórmula y ejercicios resueltos)

En este post te explicamos cómo resolver integrales con raíces. De modo que encontrarás cómo calcular la integral de una raíz y varios ejemplos de integrales de raíces resueltas paso a paso.

Índice

Fórmula de la integral de una raíz

Para calcular la integral de una raíz primero debemos transformar la raíz en una potencia y luego aplicar la fórmula de la integral de una potencia.

En definitiva, la fórmula de la integral de una raíz es la siguiente:

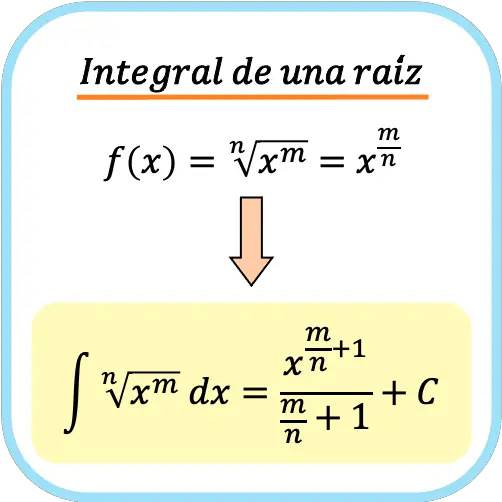
Por ejemplo, la integral de la raíz de x es igual a x elevado a tres medios dividido por tres medios.

$\displaystyle\int \sqrt{x}\ dx=\int x^{\frac{1}{2}} \ dx=\cfrac{x^{\frac{1}{2}+1}}{\frac{1}{2}+1}+C=\cfrac{x^{\frac{3}{2}}}{\frac{3}{2}}+C=\cfrac{2x^{\frac{3}{2}}}{3}+C$

➤ Ver: Derivada de una potencia

Ejemplos de integrales de raíces

Ahora que ya sabemos cuál es la fórmula de la integral de una raíz, vamos a ver varios ejemplos resueltos de integrales de raíces para que puedas ver cómo se calculan este tipo de integrales.

Ejemplo 1: Integral de la raíz cúbica de x

$\displaystyle\int \sqrt[3]{x}\ dx$

Para hallar la integral de la raíz cúbica de x simplemente tenemos que aplicar la fórmula que se ha explicado más arriba:

$\displaystyle\int \sqrt[n]{x^m}=\int x^\frac{m}{n}=\cfrac{x^{\frac{m}{n}+1}}{\frac{m}{n}+1}+C$

Por lo tanto, la integral de la raíz cúbica de x es igual a x elevado a cuatro tercios dividido por cuatro tercios.

$\begin{aligned}&\displaystyle\int \sqrt[3]{x}\ dx= \int x^{\frac{1}{3}}\ dx=\\[2ex]&=\cfrac{x^{\frac{1}{3}+1}}{\frac{1}{3}+1}+C=\cfrac{x^{\frac{4}{3}}}{\frac{4}{3}}+C=\\[2ex]&=\cfrac{3x^{\frac{4}{3}}}{4}+C=\cfrac{3\sqrt[3]{x^4}}{4}+C\end{aligned}$

Ejemplo 2: Integral de una raíz en el denominador

$\displaystyle\int \cfrac{1}{\sqrt{x^5}}\ dx$

Cuando tenemos una raíz en el denominador de una fracción tenemos que pasarla a forma de potencia y luego transformar la potencia para que pase a estar en el numerador. Para ello, basta con cambiarle el signo al exponente de la potencia:

$\displaystyle\int \cfrac{1}{\sqrt{x^5}}\ dx=\int \cfrac{1}{x^{\frac{5}{2}}}\ dx=\int x^{-\frac{5}{2}}\ dx$

Y una vez hemos eliminado la fracción y el radical de la integral, simplemente tenemos que utilizar la fórmula que hemos visto al principio del post:

$\begin{aligned}&\displaystyle\int x^{-\frac{5}{2}}\ dx=\cfrac{x^{-\frac{5}{2}+1}}{-\frac{5}{2}+1}+C=\\[2ex]&=\cfrac{x^{-\frac{3}{2}}}{-\frac{3}{2}}+C=-\cfrac{2x^{-\frac{3}{2}}}{3}+C=\\[2ex]&=-\cfrac{2}{3\sqrt{x^3}}+C\end{aligned}$

Ejemplo 3: Integral de la raíz de un polinomio

$\displaystyle\int \sqrt[5]{x+9}\ dx$

En este caso no podemos aplicar directamente la fórmula de la integración de raíces, ya que el argumento de la raíz es un polinomio de dos términos. Así pues, primero tenemos que hacer un cambio de variable:

$x+9=u$

$dx=du$

De modo que la integral con el cambio de variable queda de la siguiente manera:

$\displaystyle\int \sqrt[5]{u}\ du$

Ahora sí, aplicamos la fórmula de la integral de una raíz:

$\displaystyle\int \sqrt[5]{u}\ du=\cfrac{u^{\frac{1}{5}+1}}{\frac{1}{5}+1}+C=\cfrac{u^{\frac{6}{5}}}{\frac{6}{5}}+C=\cfrac{5u^{\frac{6}{5}}}{6}+C$

Y finalmente deshacemos el cambio de variable:

$\displaystyle\cfrac{5\left(x+9\right)^{\frac{6}{5}}}{6}+C$

➤ Ver: Integrales de funciones irracionales

Ejercicios resueltos de integrales de raíces

Calcula las integrales de las siguientes funciones con raíces:

$\text{A) } \displaystyle\int \sqrt[4]{x^7}\ dx$

$\text{B) } \displaystyle\int \sqrt{16x^9}\ dx$

$\text{C) } \displaystyle\int \cfrac{2}{\sqrt[6]{x^3}}\ dx$

$\text{D) } \displaystyle\int \cfrac{1}{\sqrt{x^3}\sqrt[5]{x^2}}\ dx$

$\text{E) } \displaystyle\int \sqrt[6]{5x+2}\ dx$

Ver solución

$\text{A) } \displaystyle\int \sqrt[4]{x^7}\ dx=\int x^{\frac{7}{4}}\ dx=\cfrac{x^{\frac{7}{4}+1}}{\frac{7}{4}+1}+C=\cfrac{x^{\frac{11}{4}}}{\frac{11}{4}}+C=\cfrac{4x^{\frac{11}{4}}}{11}+C$

$\begin{aligned}\text{B) } &\displaystyle\int \sqrt{16x^9}\ dx=\int \sqrt{16}\cdot x^{\frac{9}{2}}\ dx=4\int x^{\frac{9}{2}}\ dx=\\[2ex]&=4\cdot \cfrac{x^{\frac{9}{2}+1}}{\frac{9}{2}+1}+C=4\cdot\cfrac{x^{\frac{11}{2}}}{\frac{11}{2}}+C=\\[2ex]&=\cfrac{8x^{\frac{11}{2}}}{11}+C=\cfrac{8\sqrt{x^{11}}}{11}\end{aligned}$

$\begin{aligned}\text{C) } &\displaystyle\int \cfrac{2}{\sqrt[6]{x^3}}\ dx=2\int x^{-\frac{3}{6}}\ dx=\\[2ex]&=2\cdot\cfrac{x^{-\frac{3}{6}+1}}{-\frac{3}{6}+1}+C=2\cdot\cfrac{x^{\frac{3}{6}}}{\frac{3}{6}}+C=\cfrac{12x^{\frac{3}{6}}}{3}+C=\\[2ex]&=4x^\frac{1}{2}+C=4\sqrt{x}+C\end{aligned}$

$\begin{aligned}\text{D) } &\displaystyle\int \cfrac{1}{\sqrt{x^3}\sqrt[5]{x^2}}\ dx=\int x^{-\frac{3}{2}}\cdot x^{-\frac{2}{5}}\ dx=\int x^{-\frac{19}{10}}\ dx=\\[2ex]&=\cfrac{x^{-\frac{19}{10}+1}}{-\frac{19}{10}+1}+C=\cfrac{x^{-\frac{9}{10}}}{-\frac{9}{10}}+C=\\[2ex]&=-\cfrac{10x^{-\frac{9}{10}}}{9}+C=-\cfrac{10}{9\sqrt[10]{x^9}}+C\end{aligned}$

$\begin{aligned}\text{E) } &\displaystyle\int \sqrt[6]{5x+2}\ dx=\int \sqrt[6]{u}\ 5du=\\[2ex]&=5\cdot \cfrac{u^{\frac{1}{6}+1}}{\frac{1}{6}+1}+C=5\cdot \cfrac{u^{\frac{7}{6}}}{\frac{7}{6}}+C=\\[2ex]&=\cfrac{5\left(5x+2\right)^{\frac{7}{6}}}{\frac{7}{6}}+C=\cfrac{30\left(5x+2\right)^{\frac{7}{6}}}{7}+C=\cfrac{30\sqrt[6]{\left(5x+2\right)^7}}{7}+C\end{aligned}$

➤ Ver: Funciones con raíces