▷ Funciones definidas a Trozos (o por Partes): gráfica, ejercicios,...

En esta página encontrarás todo sobre las funciones definidas a trozos: qué son, cómo calcular su imagen y su dominio, cómo representarlas en una gráfica, su continuidad, etc. Además, verás ejemplos y podrás practicar con ejercicios resueltos paso a paso de funciones definidas a trozos.

Índice

¿Qué es una función definida a trozos?

La definición de función definida a trozos es la siguiente:

En matemáticas, una función definida a trozos es una función cuya expresión cambia según el valor que toma la variable independiente x.

Por ejemplo, la siguiente función está definida a trozos:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} x+2 & \text{si} & x<1 \\[2ex] -2x+8 & \text{si} & x \geq 1 \end{array} \right.$

Como puedes ver, la función tiene dos tramos distintos: si $x$ es más pequeña que 1 la función valdrá $x+2$ , por contra, si $x$ es más grande o igual que 1 la función valdrá $-2x+8.$

Aunque más abajo veremos cómo se representan, a continuación tienes el gráfico de esta función definida a trozos:

Las funciones definidas a trozos también reciben el nombre de funciones definidas por partes o pedazos, funciones seccionadas, funciones segmentadas, funciones multipartes, funciones por intervalos,… entre otros.

Imagen de una función definida a trozos

Para calcular la imagen de una función definida por partes tenemos que coger la expresión del intervalo al que pertenece la variable.

Así escrito puede sonar muy complicado, pero con un ejemplo verás que es fácil:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} x+2 & \text{si} & x \leq 0 \\[2ex] 5 & \text{si} & 0 <x<4 \\[2ex] 2x^2-4 & \text{si} & x\geq4 \end{array} \right.$

Esta función definida a trozos quiere decir que si $x$ es más pequeña o igual que 0 la función valdrá $x+2$ , en cambio, entre $x=0$ (no incluido) y $x=4$ (no incluido) la función siempre valdrá 5, y finalmente, a partir de $x=4$ (incluido) la función tomará el valor de $2x^2-4.$

Entonces si, por ejemplo, queremos calcular $f(-3)$ tenemos que coger la expresión de $x\le0$ , porque -3 es más pequeño que 0:

$f(-3)=-3+2=-1$

O si queremos determinar $f(2)$ tenemos que coger la expresión del intervalo $0<x<4$ , porque $x=2$ se encuentra dentro de ese intervalo:

$f(2)=5$

Y si deseamos hallar $f(4)$ tenemos que hacerlo con la última expresión, ya que $x=4$ pertenece a ese intervalo:

$f(4)=2\cdot 4^2-4=32-4=28$

Dominio de una función definida a trozos

El dominio de una función definida a tramos es la unión de los diferentes subdominios asociados a cada una de sus ramas.

Por ejemplo, para determinar el dominio de la siguiente función definida por intervalos debemos calcular el dominio de cada subfunción:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2-3x+1 & \text{si} & x\leq 2 \\[2ex] \cfrac{3}{x-5} & \text{si} & x>2 \end{array} \right.$

El primer tramo es una función polinómica, por lo tanto, su dominio son todos los números reales (hasta x=2).

$f_1= x^2-3x+1$

$\text{Dom } f_1= (-\infty,2]$

La segunda rama corresponde a una función racional, por lo que debemos hallar qué número anula el denominador ya que ese número será el único que no formará parte del dominio:

$f_2= \cfrac{3}{x-5}$

$x-5=0$

$x=5$

$\text{Dom } f_2= (2,5)\cup (5,+\infty)$

De modo que el dominio de toda la función definida a trozos es la unión de los dos subdominios:

$\text{Dom } f=(-\infty,2] \cup (2,5)\cup (5,+\infty)$

$\text{Dom } f= (-\infty,5) \cup (5,+\infty)$

O equivalentemente:

$\text{Dom } f= \mathbb{R} - \{5\}$

Cómo representar gráficamente una función definida a trozos

Representar una función a trozos en una gráfica es sencillo, simplemente hay que representar cada intervalo por separado. Veamos cómo graficar una función definida a trozos mediante un ejemplo:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} -x+4 & \text{si} & x<1 \\[2ex] x^2-4x+4 & \text{si} & 1 \leq x<4 \\[2ex] 5 & \text{si} & x\geq 4 \end{array} \right.$

En primer lugar, debemos representar la función del primer tramo, que se trata de una función afín. Así que hacemos una tabla de valores y, evidentemente, para ello únicamente podemos coger valores de $x$ que estén dentro del primer intervalo:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} \color{blue}\boxed{\color{black}-x+4} & \text{si} & x<1 \\[2ex] x^2-4x+4 & \text{si} & 1 \le x<4 \\[2ex] 5 & \text{si} & x\ge 4 \end{array} \right.$

$x= -2 \ \longrightarrow \ f(x) = -(-2)+4=6$

$x= -1 \ \longrightarrow \ f(x) =-(-1)+4=5$

$x= 0 \ \longrightarrow \ f(x) =-0+4=4$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 6 \\ -1 & 5 \\ 0 & 4 \end{array}$

Ahora representamos los puntos en la gráfica y trazamos la recta:

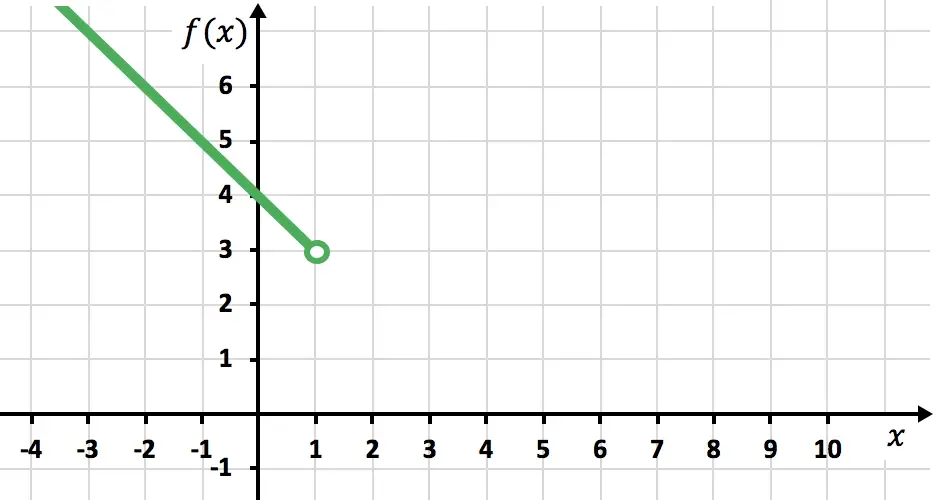
como representar una funcion definida a trozos primer tramo

En este tramo el 1 no está incluido, ya que el símbolo $"< \ "$ de $x<1$ significa estrictamente más pequeño que uno. Por lo tanto, debemos poner un punto abierto en $x=1$ para indicar que no está incluido.

Una vez hemos representado el primer tramo, representaremos el segundo tramo, que va desde $x=1$ (incluido) hasta $x=4$ (no incluido):

$\displaystyle f(x)= \left\{ \begin{array}{lcl} -x+4 & \text{si} & x<1 \\[2ex] \color{blue}\boxed{\color{black}x^2-4x+4} & \text{si} & 1 \leq x<4 \\[2ex] 5 & \text{si} & x\geq 4 \end{array} \right.$

Se trata de una función cuadrática, así que primero calculamos el vértice de la parábola (mediante su fórmula) y luego construimos una tabla de valores alrededor del vértice:

$x = \cfrac{-b}{2a} = \cfrac{-(-4)}{2\cdot 1}= \cfrac{4}{2}= 2$

$x= 2 \ \longrightarrow \ f(2) = 2^2-4\cdot 2+4=0$

$x= 1 \ \longrightarrow \ f(1) = 1^2-4\cdot 1+4=1$

$x= 3 \ \longrightarrow \ f(3) = 3^2-4 \cdot 3+4=1$

$x= 4 \ \longrightarrow \ f(4) = 4^2-4\cdot 4+4=4$

$\begin{array}{c|c} x & f(x) \\ \hline 2 & 0 \\ 1 & 1 \\ 3 & 1 \\ 4&4 \end{array}$

Representamos los puntos obtenidos en la cuadrícula y trazamos la parábola:

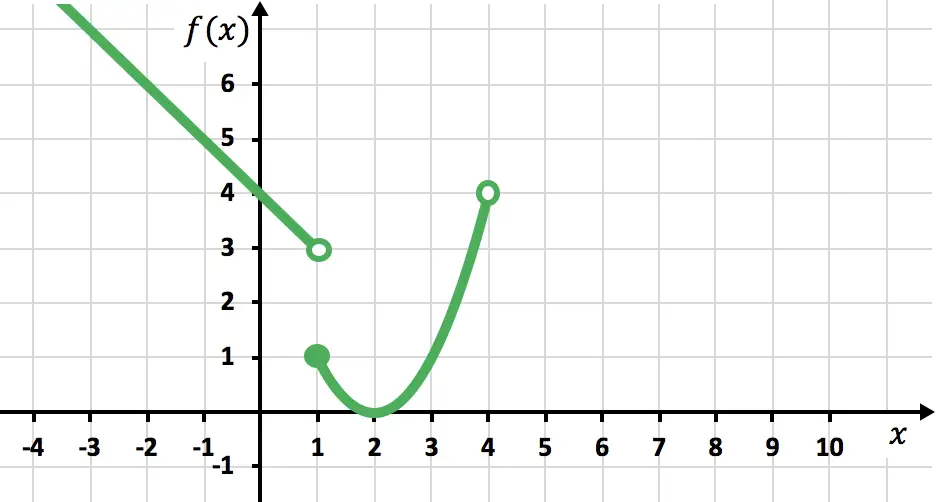
como graficar una funcion definida a trozos segundo tramo

Fíjate que hemos representado la parábola con un punto cerrado al principio y un punto abierto al final. Eso es debido a que el intervalo $1 \le x < 4$ está definido primero con el signo $"\le \ "$ cosa que significa que el 1 está incluido (porque también tiene el signo igual) y, por tanto, debemos poner un punto cerrado. En cambio, el signo $"< \ "$ indica que el 4 no está incluido y por eso hay que poner un punto abierto.

Y finalmente representamos el último tramo:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} -x+4 & \text{si} & x<1 \\[2ex] x^2-4x+4 & \text{si} & 1 \leq x<4 \\[2ex] \color{blue}\boxed{\color{black}5} & \text{si} & x\geq 4 \end{array} \right.$

En este intervalo la función es constante y siempre vale 5. Por tanto, dibujamos una recta en $f(x)=5$ a partir de $x=4$ :

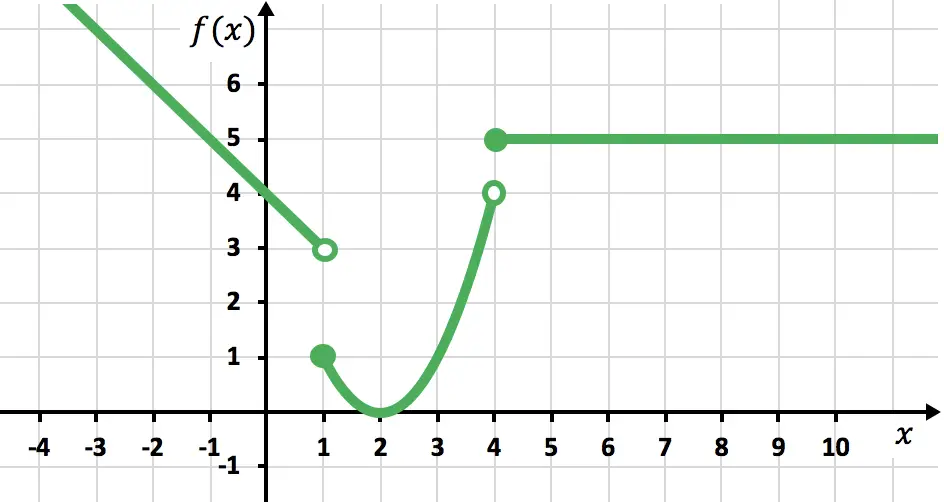
representacion grafica de una funcion definida a trozos

A diferencia de antes, en este tramo sí que está incluido $x=4$ , porque la expresión $x\ge 4$ tiene el signo $"\ge \ "$ . Por tanto, debemos representarlo con un punto cerrado para indicar que también se incluye este punto.

Y de esta manera ya hemos acabado la representación gráfica de la función definida a trozos. Como ves no es muy complicado, simplemente hay que representar cada tramo por separado en un mismo gráfico.

Continuidad de una función definida a trozos

Según el concepto de continuidad, una función es continua en un punto si existen los límites laterales en dicho punto y, además, son iguales a su imagen.

$\lim\limits_{x \to a^-} f(x)=\lim\limits_{x \to a^+} f(x)= f(a)$

Entonces, para que una función definida a trozos sea continua se debe cumplir la condición anterior en todos los puntos de cada tramo y, además, en los puntos donde se cambia de tramo.

A modo de ejemplo, vamos a analizar la continuidad de la siguiente función definida por intervalos:

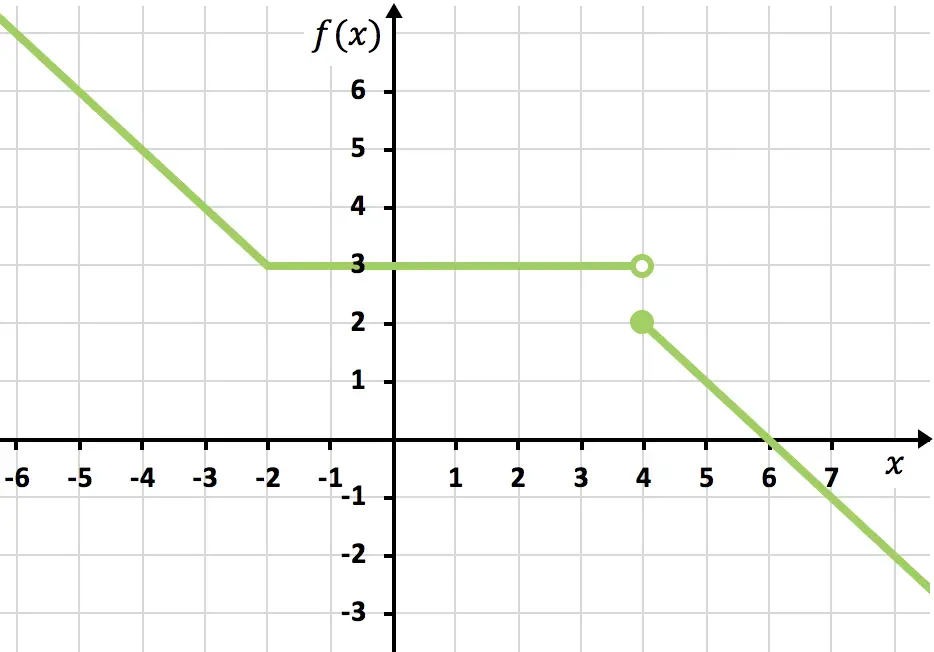
continuidad de una funcion definida a trozos

La función es continua en $x=-2,$ ya que se cumple la condición de continuidad:

$\lim\limits_{x \to -2^-} f(x)=\lim\limits_{x \to -2^+} f(x)= f(-2)=3$

De hecho, como la función es continua en este punto, se han unido los extremos de los dos intervalos.

Sin embargo, la función es discontinua en $x=4$ porque no se verifica la condición de continuidad:

$\lim\limits_{x \to 4^-} f(x)=3 \neq \lim\limits_{x \to 4^+} f(x)= 2$

En definitiva, la función definida por partes es continua en todos los números reales excepto en $x=4,$ donde tiene una discontinuidad.

Puedes practicar de hacer más ejercicios de este tipo haciendo click en el siguiente enlace:

➤ Ver: ejercicios resueltos de la continuidad de una función

Ejercicios resueltos de funciones definidas a trozos

Ejercicio 1

A partir de la siguiente función definida a trozos:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 1 & \text{si} & x<-3 \\[2ex] x+4 & \text{si} & -3 \leq x \leq 5 \\[2ex] 3x-6 & \text{si} & x>5 \end{array} \right.$

Calcula:

$f(-4)$
$f(2)$
$f(7)$

Ver solución

La función siempre vale 1 si $x$ es más pequeña que -3. Por tanto:

$f(-4)= \mathbf{1}$

En cambio, $x=2$ está en el intervalo entre -3 y 5. Por tanto debemos hacer el cálculo con la función del segundo tramo:

$f(2)=2+4=\mathbf{6}$

Por último, $x=7$ es más grande que 5. Con lo que debemos hacer el cálculo con la función del tercer tramo:

$f(7)=3\cdot 7-6 = 21 - 6 = \mathbf{15}$

Ejercicio 2

A partir de la siguiente función definida a trozos:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-5x-2 & \text{si} & x \leq -1 \\[2ex] 3x-7 & \text{si} & -1<x \leq 4 \\[2ex] 2 & \text{si} & x>4 \end{array} \right.$

Calcula las siguientes imágenes:

$f(-2)$
$f(3)$
$f(4)$

Ver solución

En primer lugar, $x=-2$ es más pequeño que -1. Por tanto debemos hacer el cálculo con la función del primer tramo:

$f(-2)=3\cdot (-2)^2-5\cdot (-2)-2=3 \cdot 4+10-2=\mathbf{20}$

En cambio, $x=3$ está dentro del intervalo entre -1 y 4. Por lo que debemos hacer el cálculo con la función del segundo tramo:

$f(3)=3\cdot 3-7 =9-7= \mathbf{2}$

Por último, $x=4$ justo separa el segundo del tercer intervalo. Pero como el segundo intervalo es $-1<x\le4$ significa que el 4 está incluido en el segundo intervalo, ya que el signo que está al lado del 4 (≤) indica que también está incluido. Por tanto, debemos hacer el cálculo con la función del segundo tramo:

$f(4)=3\cdot 4-7 =12-7= \mathbf{5}$

Ejercicio 3

Representa la siguiente función definida a trozos en una gráfica:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 4 & \text{si} & x<-1 \\[2ex] x+1 & \text{si} & -1 \leq x \leq 4 \\[2ex] 3 & \text{si} & x>4 \end{array} \right.$

Ver solución

Primer tramo

$\displaystyle f(x)= \left\{ \begin{array}{lcl} \color{blue}\boxed{\color{black}4} & \text{si} & x<-1 \\[2ex] x+1 & \text{si} & -1 \leq x \leq 4 \\[2ex] 3 & \text{si} & x>4 \end{array} \right.$

$f(x)$ siempre vale 4 cuando $x$ es más pequeña que -1. Por tanto dibujamos una recta en $f(x)= 4$ hasta $x=-1 :$

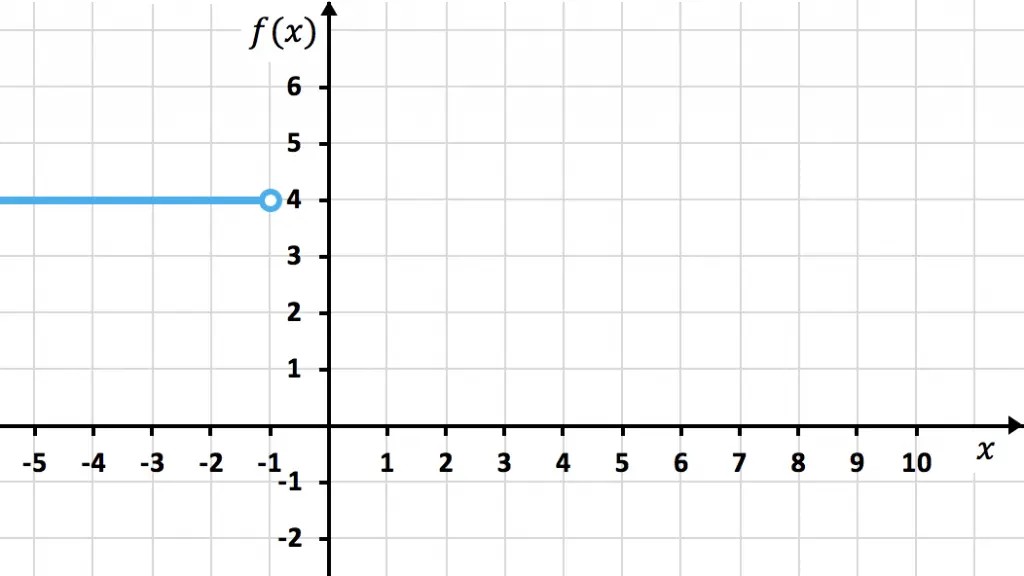
Y representamos el punto de $x=-1$ con un punto abierto, ya que el intervalo tiene el signo <.

Segundo tramo

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 4 & \text{si} & x<-1 \\[2ex] \color{blue}\boxed{\color{black}x+1} & \text{si} & -1 \leq x \leq 4 \\[2ex] 3 & \text{si} & x>4 \end{array} \right.$

El segundo trozo corresponde a una función lineal, así que hacemos una tabla de valores para dibujarla:

$x=0 \longrightarrow f(0)=0+1=1$

$x=1 \longrightarrow f(1)=1+1=2$

$x=2 \longrightarrow f(2)=2+1=3$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \end{array}$

Representamos los puntos en el gráfico y trazamos la recta del tramo:

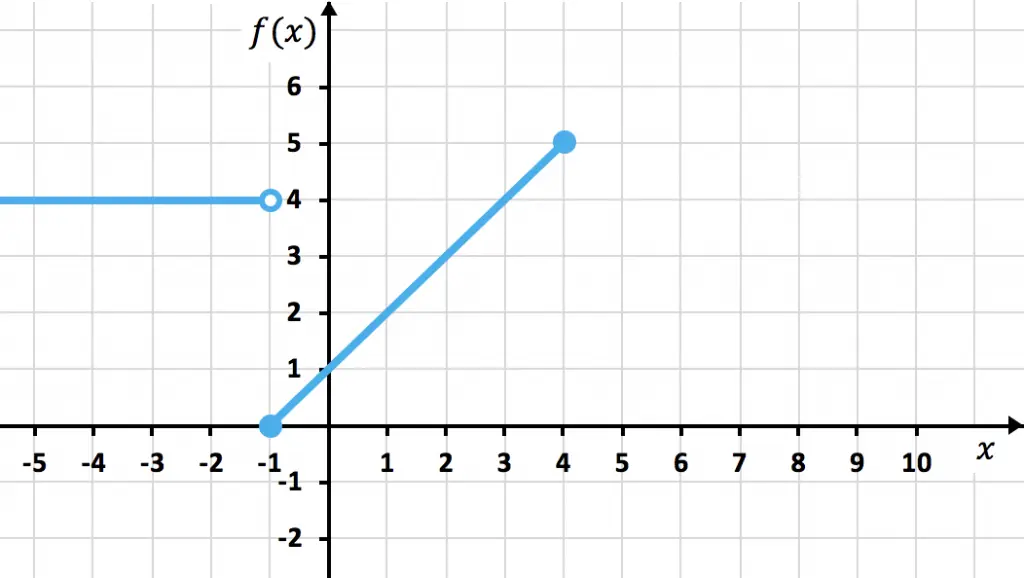
Y representamos los dos extremos con puntos cerrados, porque ambos tienen el signo ≤ en el intervalo.

Tercer tramo

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 4 & \text{si} & x<-1 \\[2ex] x+1 & \text{si} & -1 \leq x \leq 4 \\[2ex] \color{blue}\boxed{\color{black}3} & \text{si} & x>4 \end{array} \right.$

La función siempre vale 3 cuando $x$ es más grande que 4. Por tanto dibujamos una recta en $f(x)= 3$ a partir de $x=4 :$

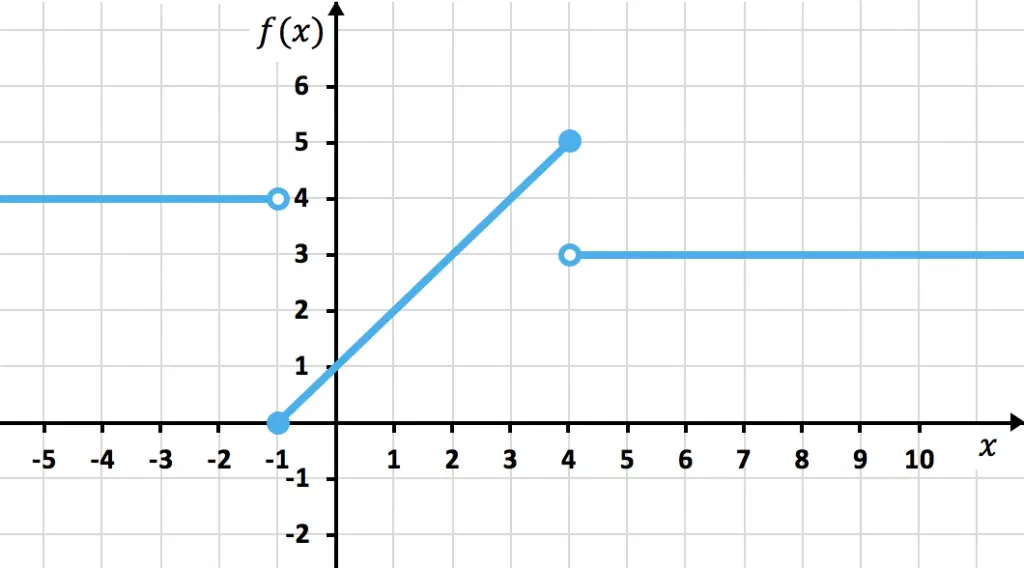
ejercicios resueltos de funciones definidas a trozos

Y representamos el punto de $x=4$ con un punto abierto, ya que el intervalo tiene el signo >.

Ejercicio 4

Representa la siguiente función definida a trozos en una gráfico:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2+2x+2 & \text{si} & x\leq 1 \\[2ex] -x+8 & \text{si} & x>1 \end{array} \right.$

Ver solución

Primer tramo

$\displaystyle f(x)= \left\{ \begin{array}{lcl} \color{blue}\boxed{\color{black} x^2+2x+2 } & \text{si} & x\leq 1 \\[2ex] -x+8 & \text{si} & x>1 \end{array} \right.$

La expresión del primer tramo se trata de una función cuadrática, por tanto, primero calculamos el vértice de la parábola con su fórmula:

$x = \cfrac{-b}{2a} = \cfrac{-2}{2\cdot 1} = -1$

Ahora creamos la tabla de valores. Para ello calculamos el valor de $f(x)$ en el vértice y alrededor del vértice:

$x= -1 \ \longrightarrow \ f(-1)=(-1)^2+2(-1)+2 = 1$

$x= 0 \ \longrightarrow \ f(0)=0^2+2\cdot 0+2 =2$

$x= -2 \ \longrightarrow \ f(-2)=(-2)^2+2(-2)+2 = 2$

$x= -3 \ \longrightarrow \ f(-3)=(-3)^2+2(-3)+2 = 5$

$x= 1 \ \longrightarrow \ f(1)=1^2+2\cdot 1+2 = 5$

$\begin{array}{c|c} x & f(x) \\ \hline -1 & 1 \\ 0 & 2 \\ -2 & 2 \\ 1 & 5 \\ -3 & 5 \end{array}$

Representamos los puntos en el gráfico y trazamos la parábola en el intervalo $x\le1 :$

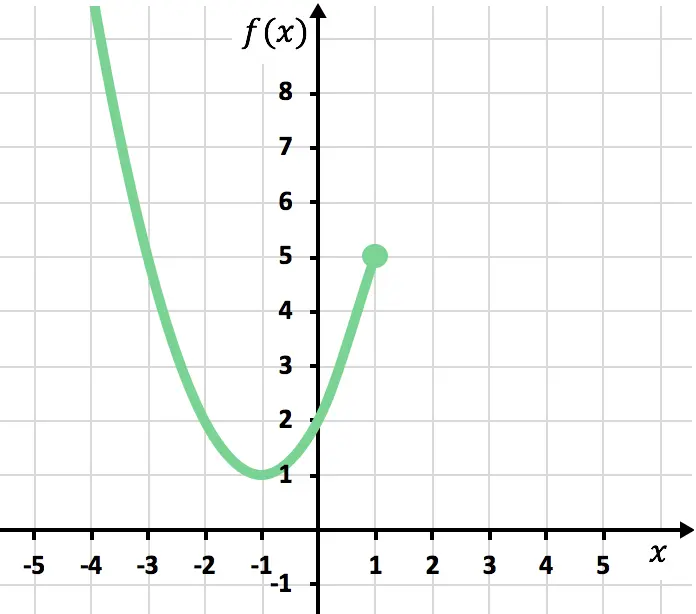
Y representamos el punto de $x=1$ con un punto cerrado, ya que el intervalo tiene el signo ≤.

Segundo tramo

$\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2+2x+2 & \text{si} & x\leq 1 \\[2ex] \color{blue}\boxed{\color{black}-x+8 }}}& \text{si} & x>1 \end{array} \right.$

La función del segundo tramo es una función afín, así que hacemos una tabla de valores para representarla:

$x= 1 \ \longrightarrow \ f(1)=-1+8=7$

$x= 2 \ \longrightarrow \ f(2)=-2+8=6$

$x= 3 \ \longrightarrow \ f(3)=-3+8=5$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 7 \\ 2 & 6 \\ 3 & 5 \end{array}$

Representamos los puntos en el gráfico y trazamos la recta en el intervalo $x>-1 :$

funcion definida a trozos con una funcion cuadratica

Y representamos el punto de $x=1$ con un punto abierto, ya que el intervalo tiene el signo >.

Ejercicio 5

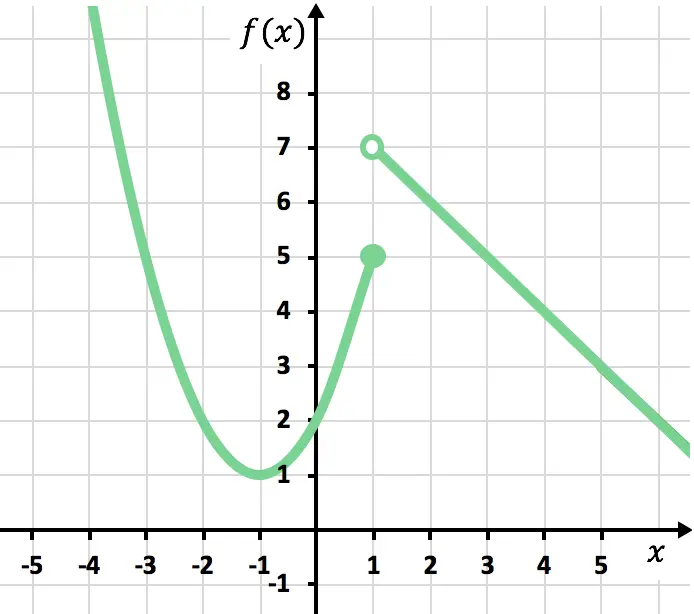
Realiza la representación gráfica de la siguiente función definida a trozos:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} -x^2-4x+1 & \text{si} & x<-2 \\[2ex] 3 & \text{si} & -2\leq x<4 \\[2ex] 2x-10 & \text{si} & x \geq 4 \end{array} \right.$

Ver solución

Primer tramo

$\displaystyle f(x)= \left\{ \begin{array}{lcl} \color{blue}\boxed{\color{black}-x^2-4x+1}& \text{si} & x<-2 \\[2ex] 3 & \text{si} & -2\leq x<4 \\[2ex] 2x-10 & \text{si} & x \geq 4 \end{array} \right.$

La expresión del primer tramo consiste en una función cuadrática, por lo tanto, primero calculamos el vértice de la parábola con su fórmula:

$x = \cfrac{-b}{2a} = \cfrac{-(-4)}{2\cdot (-1)} = \cfrac{+4}{-2} = -2$

Ahora creamos la tabla de valores. Para ello calculamos el valor de $f(x)$ en el vértice y alrededor del vértice:

$x= -2 \ \longrightarrow \ f(-2)=-(-2)^2-4(-2)+1 =5$

$x= -3 \ \longrightarrow \ f(-3)=-(-3)^2-4(-3)+1 =4$

$x= -4 \ \longrightarrow \ f(-4)=-(-4)^2-4(-4)+1 =1$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 5 \\ -3 & 4 \\ -4 & 1 \end{array}$

Representamos los puntos en el gráfico y trazamos la parábola en el intervalo $x<-2 :$

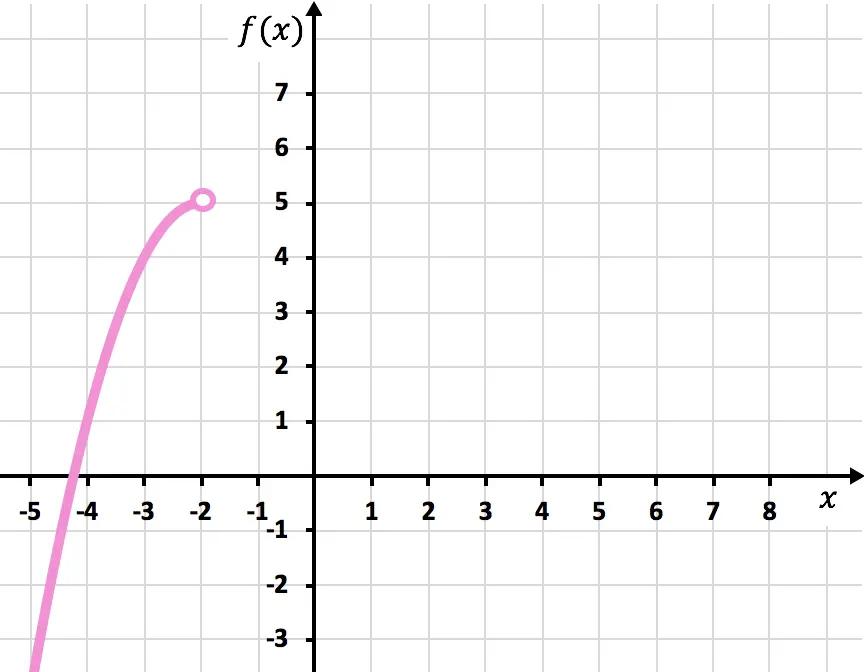
Y representamos el punto de $x=-2$ con un punto abierto, ya que el intervalo tiene el signo <.

Segundo tramo

$\displaystyle f(x)= \left\{ \begin{array}{lcl} -x^2-4x+1 & \text{si} & x<-2 \\[2ex] \color{blue}\boxed{\color{black}3} & \text{si} & -2\leq x<4 \\[2ex] 2x-10 & \text{si} & x \geq 4 \end{array} \right.$

La función siempre vale 3 cuando $x$ está entre -2 (incluido) y 4 (no incluido). Por tanto dibujamos una recta en $f(x)= 3$ en el intervalo $-2 \le x < 4 :$

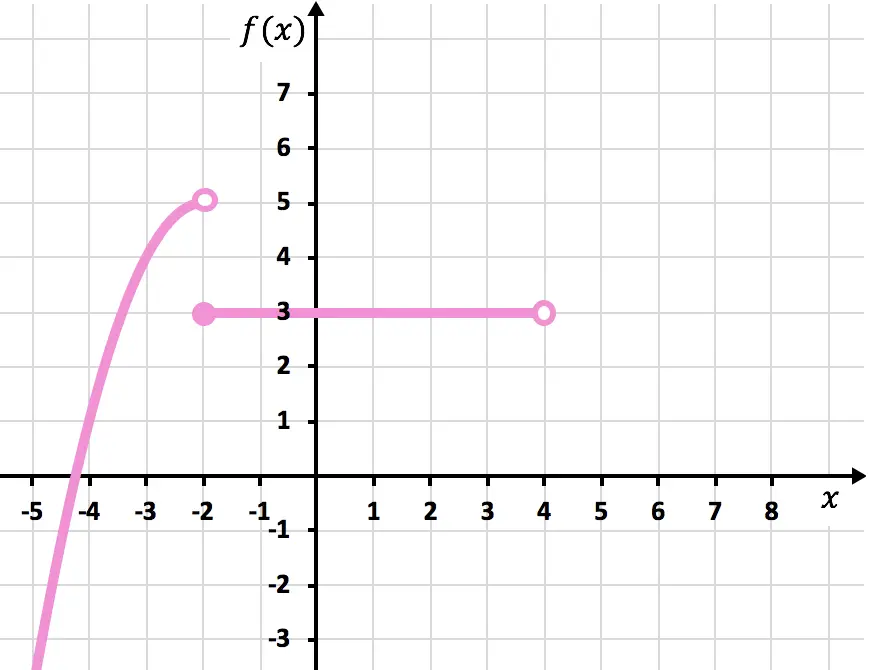
Representamos el extremo de $x=-2$ con un punto cerrado, ya que el -2 tiene el signo ≤ en el intervalo. En cambio, representamos el extremo de $x=-4$ con un punto abierto, porque el 4 tiene el signo < en el intervalo.

Tercer tramo

$\displaystyle f(x)= \left\{ \begin{array}{lcl} -x^2-4x+1 & \text{si} & x<-2 \\[2ex] 3 & \text{si} & -2\leq x<4 \\[2ex] \color{blue}\boxed{\color{black} 2x-10} & \text{si} & x \geq 4 \end{array} \right.$

La tercera subfunción es una función afín, así que hacemos una tabla de valores:

$x=4 \longrightarrow f(4)=2\cdot 4-10=-2$

$x=5 \longrightarrow f(5)=2\cdot 5-10=0$

$x=6 \longrightarrow f(6)=2\cdot 6-10=2$

$\begin{array}{c|c} x & f(x) \\ \hline 4 & -2 \\ 5 & 0 \\ 6 & 2 \end{array}$

Representamos los puntos en el gráfico y trazamos la recta en el intervalo $x\ge 4 :$

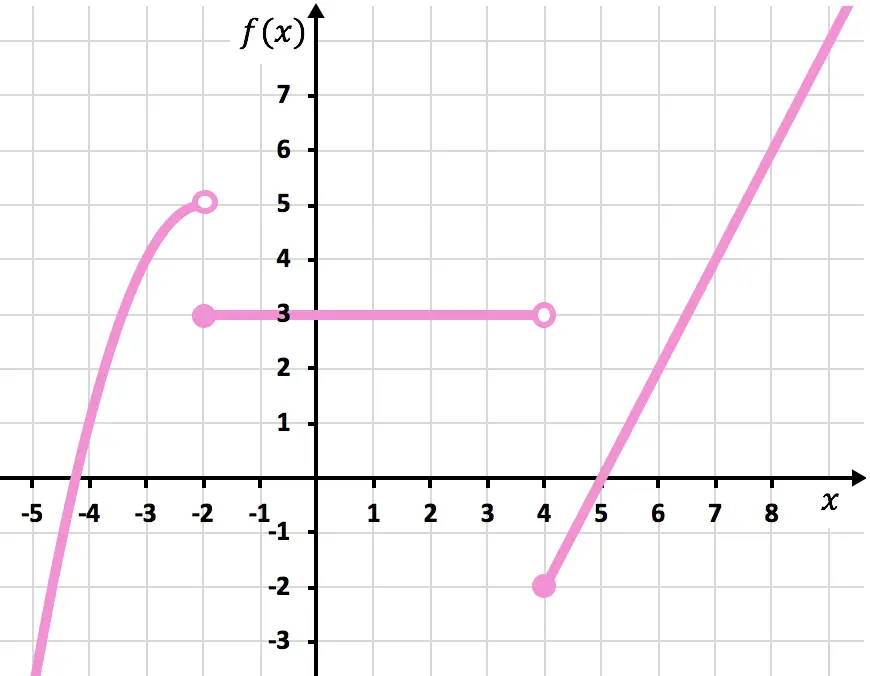
ejercicios resueltos de funciones definidas por partes

Y representamos el punto de $x=4$ con un punto cerrado, ya que el intervalo tiene el signo ≥.

Ejercicio 6

Determina a qué función a trozos corresponde el siguiente gráfico:

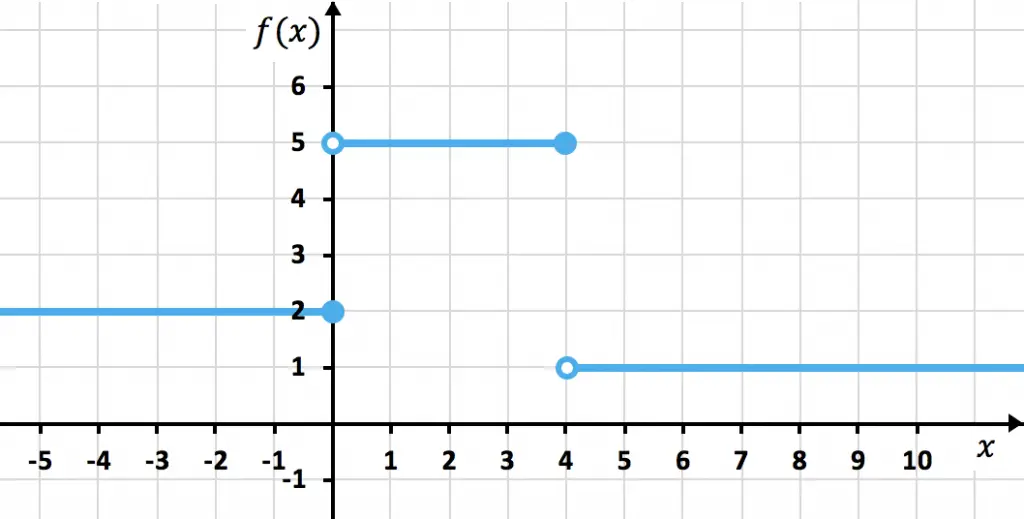
ejemplo de funcion definida por intervalos

Ver solución

En el primer tramo, cuando x≤0, la función siempre vale 2. En este intervalo debemos poner el signo ≤ porque hay un punto cerrado en x=0.

En el segundo tramo la función siempre vale 5. Y va desde x=0 (no incluido) hasta x=4 (incluido).

Finalmente en el tercer tramo, cuando x>4, la función siempre vale 1. Además debemos poner el signo > porque hay un punto abierto en x=4.

De modo que la función definida a trozos es:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 2 & \text{si} & x\leq 0 \\[2ex] 5 & \text{si} & 0 <x\leq 4 \\[2ex] 1 & \text{si} & x>4 \end{array} \right.$

Ejercicio 7

Determina la función por partes cuya gráfica es la siguiente:

Ver solución

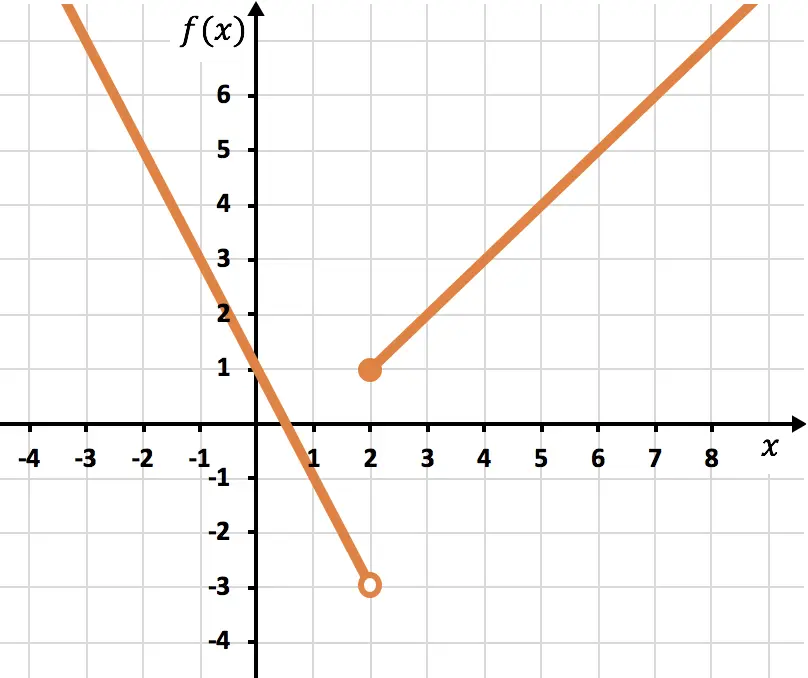
Primer tramo

La función del primer tramo es una función afín, por tanto, será de la siguiente forma:

$f(x)=mx+n$

Para hallar la definición de la función debemos coger dos puntos por los que pasa la recta, por ejemplo (0,1) y (1,-1) .[/latex] Ahora, mediante la fórmula de la pendiente, podemos calcular la pendiente m de la función con estos dos puntos:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{-1-1}{1-0} = \cfrac{-2}{1} = -2$

De manera que la función será de la forma:

$f(x)=mx+n \ \xrightarrow{m \ = \ -2} \ f(x)=-2x+n$

Y una vez sabemos m podemos calcular el coeficiente n. Para ello sustituimos las coordenadas de un punto que pertenezca a la función en la ecuación. Por ejemplo el punto (0,1):

$f(x)=-2x+n \ \xrightarrow{x \ = \ 0 \ ; \ f(x) \ = \ 1} \ 1=-2\cdot 0+n$

Resolvemos la ecuación resultante:

$1=0+n$

$1=n$

Por tanto la función del primer tramo es:

$\bm{f(x)=-2x+1}$

Este tramo corresponde a todas las $x$ hasta 2 (no incluido), es decir, a todos los números más pequeños que 2. Así que el intervalo del primer tramo es:

$x<2$

Y ponemos el signo < porque en este caso $x=2$ está representado como un punto abierto.

Segundo tramo

La función del segundo tramo también es una función afín, por lo que debemos repetir el mismo procedimiento:

$f(x)=mx+n$

Para hallar la función debemos coger dos puntos por los que pasa la recta, por ejemplo (3,2) y (4,3). Y con estos dos puntos podemos calcular la pendiente de la función con su fórmula:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{3-2}{4-3} = \cfrac{1}{1} = 1$

De manera que la función será de la forma:

$f(x)=mx+n \ \xrightarrow{m \ = \ 1} \ f(x)=1x+n$

Y una vez conocemos m podemos calcular el término n. Para ello sustituimos las coordenadas de un punto que pertenezca a la función en la ecuación. Por ejemplo el punto (3,2):

$f(x)=x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ 2} \ 2=3+n$

Resolvemos la ecuación resultante:

$2-3=+n$

$-1=n$

Por tanto la función del segundo tramo es:

$\bm{f(x)=x-1}$

Este tramo corresponde a todas las x a partir de 2 (incluido), es decir, a todos los números más grandes o iguales que 2. Así que el intervalo del segundo tramo es:

$x\ge 2$

Y ponemos el signo ≥ porque en este tramo $x=2$ es un punto cerrado.

En conclusión, la función definida a trozos del gráfico es:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} -2x+1 & \text{si} & x<2 \\[2ex] x-1 & \text{si} & x\ge 2 \end{array} \right.$

Funciones definidas a trozos

¿Qué es una función definida a trozos?

Imagen de una función definida a trozos

Dominio de una función definida a trozos

Cómo representar gráficamente una función definida a trozos

Continuidad de una función definida a trozos

Ejercicios resueltos de funciones definidas a trozos

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

Ejercicio 6

Ejercicio 7

Deja un comentario Cancelar respuesta