En este post te explicamos qué son las funciones de proporcionalidad directa, cuál es su fórmula, cómo representarlas en una gráfica y cómo calcular su ecuación a partir de un punto dado.
Índice
¿Qué es una función de proporcionalidad directa?
La función de proporcionalidad directa es una función que relaciona dos magnitudes directamente proporcionales. Por lo tanto, para calcular el valor de la variable dependiente (y) se debe multiplicar el valor la variable dependiente (x) por la constante de proporcionalidad.
La función de proporcionalidad directa también se llama función lineal.
Recuerda que dos magnitudes son directamente proporcionales si una de las magnitudes aumenta de valor cuando la otra magnitud también aumenta, y al revés.
Fórmula de la función de proporcionalidad directa
La fórmula que define la función de proporcionalidad directa es la siguiente:
Donde y es la variable independiente, x la variable dependiente, y m es la pendiente o constante de proporcionalidad de la función.
Como puedes ver, con esta fórmula es muy fácil calcular valores de la magnitud y, simplemente tenemos que multiplicar el valor de la magnitud x por la pendiente de la función, que es característica de cada función de proporcionalidad directa.
Por ejemplo, si tenemos la siguiente función de proporcionalidad directa:
Si queremos determinar cuánto vale la magnitud y cuando x vale 5, solamente tenemos que multiplicar la pendiente de la función (3) por 5:
Representación gráfica de una función de proporcionalidad directa
A continuación, vamos a ver cómo representar gráficamente las funciones de proporcionalidad directa. Haremos el siguiente ejercicio a modo de ejemplo:
Para representar la función de proporcionalidad directa en una gráfica simplemente hay que trazar una recta que pase por el origen de coordenadas (punto (0,0)) y que tenga la pendiente de la función.
En este caso, la función que queremos representar tiene una pendiente de , por tanto, la recta debe crecer dos unidades de y por cada unidad de x.
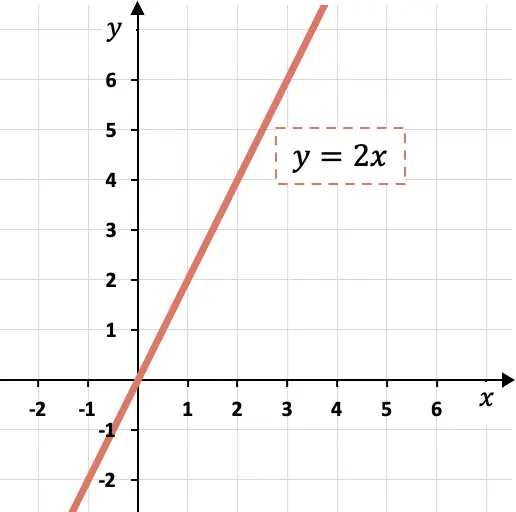
Como puedes ver en el gráfico, si la pendiente es igual a 2 significa que la magnitud y aumenta el doble que la magnitud x.
Las funciones de proporcionalidad directa tienen una gráfica muy similar a las funciones afines, sin embargo, son dos tipos de funciones diferentes. Puedes ver cuáles son las diferencias entre una función afín y una función lineal en el siguiente enlace:
➤ Ver: diferencia entre función lineal y afín
Cómo hallar la función de proporcionalidad directa
Si conocemos un punto de la función de proporcionalidad directa, podemos encontrar su ecuación fácilmente. Veamos cómo se hace resolviendo un problema de funciones de proporcionalidad directa:
- El número de habitaciones que pinta un pintor es, aproximadamente, directamente proporcional a las horas que trabaja, es decir, cuánto más horas trabaje más habitaciones podrá pintar. Si sabemos que en una jornada de 8 horas ha pintado dos habitaciones enteras, ¿cuál es la función de proporcionalidad directa que relaciona el número de habitaciones pintadas con las horas trabajadas?
En primer lugar, tenemos que determinar cuál es la variable dependiente y cuál la independiente. El número de habitaciones pintadas depende de las horas trabajadas, y no al revés. Por lo tanto, la variable independiente (x) son las horas trabajadas y la variable dependiente (y) las habitaciones pintadas.
El problema nos dice que el pintor puede pintar 2 habitaciones en 8 horas, de modo que la gráfica de la función tiene que pasar por el punto (8,2).
Además, el enunciado dice que las dos magnitudes tienen una relación proporcional directa, lo que significa que se relacionan matemáticamente con la fórmula de la función de proporcionalidad directa:
Ahora podemos calcular el valor de la pendiente de la función sustituyendo las coordenadas del punto (8,2) en la ecuación:
Y, finalmente, despejamos la incógnita m de la ecuación:
En definitiva, la función de proporcionalidad directa del problema es:
También te puede interesar:

