En este post explicamos qué es la periodicidad de una función. Además, podrás ver varios ejemplos de funciones periódicas. Finalmente, analizaremos el periodo de las funciones trigonométricas, ya que es una de sus características más importantes.
Índice
¿Qué es la periodicidad de una función?
La periodicidad de una función es una característica de las funciones que repiten sus valores de manera cíclica, es decir, una función es periódica si su gráfica se va repitiendo cada cierto intervalo. Dicho intervalo se llama periodo.
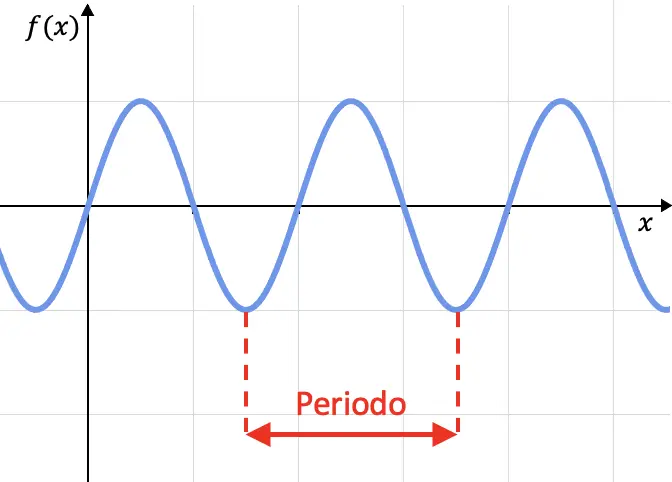
Matemáticamente, se define una función como periódica si se cumple que para cualquier valor de la variable independiente x.
Donde T es el periodo de la función periódica i k un número entero cualquiera.
Ejemplos de periodicidades de funciones
Una vez hemos visto el concepto de periodicidad de una función, vamos a ver varios ejemplos de cómo calcular la periodicidad de una función.
Ejemplo 1
Determina si la siguiente función es periódica:
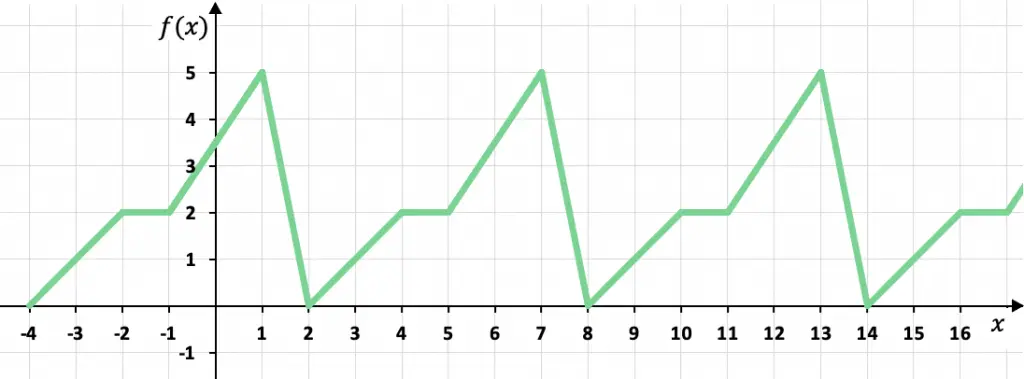
Esta función definida a trozos se trata de una función periódica, ya que los valores de su gráfica se van repitiendo cíclicamente. En concreto, la función toma el mismo valor cada seis x, por lo tanto, el periodo de la función es igual a 6.
Ejemplo 2
Halla la periodicidad de la siguiente función:
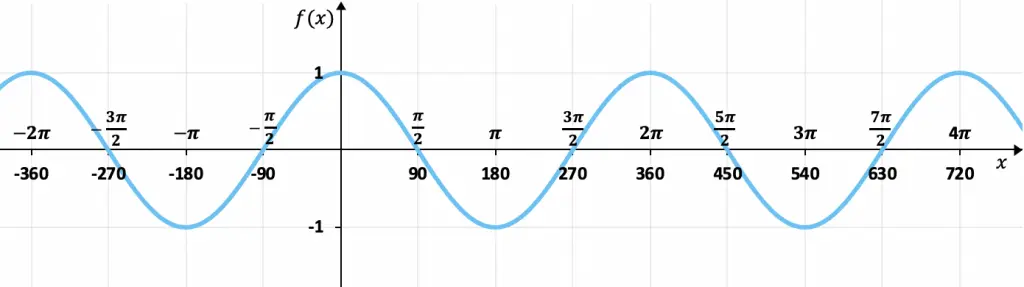
Esta función corresponde a la representación gráfica de una función trigonométrica, en concreto, de la función coseno.
Como podemos ver en el gráfico, la función repite sus valores periódicamente, por lo que es una función periódica. Además, entre pico y pico de la onda hay un espacio de 2π (o 360º), de modo que ese es el periodo de la función.
Periodicidad de funciones trigonométricas
La periodicidad y las funciones trigonométricas están muy relacionadas, de hecho, una de las principales características de este tipo de funciones es que la mayoría de funciones trigonométricas son periódicas.
A continuación, vamos a estudiar la periodicidad de las 3 funciones trigonométricas principales: el seno, el coseno y la tangente.
Periodo de la función seno
La expresión de la función seno es la siguiente:
En este caso, no es necesario representar gráficamente la función para hallar su periodo, sino que podemos calcularlo simplemente aplicando la siguiente fórmula:
Además, la función seno tiene la peculiaridad de que si modificamos su periodo también estamos cambiando la forma que tiene su gráfica. Puedes ver cómo afecta el valor del periodo a su representación gráfica en el siguiente enlace:
➤ Ver: Gráfica de la función seno
Periodo de la función coseno
La expresión algebraica de la función coseno es la siguiente:
Al igual que en el seno, se puede hallar directamente el periodo de la función coseno utilizando la siguiente fórmula:
El valor del periodo del coseno condiciona completamente a su gráfica, haz click en el siguiente enlace y descubre por qué:
➤ Ver: Gráfica de la función coseno
Periodo de la función tangente
La función tangente se describe matemáticamente:
El periodo de la función tangente se calcula con la misma fórmula que la del seno y el coseno:
Sin embargo, la gráfica de la función tangente es diferente al seno y al coseno, porque también tiene asíntotas que se van repitiendo de manera periódica. Puedes ver esto y más características de esta función trigonométrica en el siguiente enlace:
➤ Ver: Gráfica de la función tangente
