▷ Integrales y derivadas

En este artículo te explicamos qué son las derivadas y las integrales y cuál es la relación entre estas dos operaciones matemáticas. Además, podrás ver las fórmulas que permiten integrar o derivar funciones.

Índice

Derivadas

Las derivadas son reglas matemáticas que sirven para estudiar las funciones. En particular, la derivada de una función en un punto es el resultado de un límite e indica el comportamiento de la función en ese punto.

La derivada de una función se expresa con el signo prima ‘, es decir, la función f'(x) es la derivada de la función f(x).

Geométricamente, el significado de la derivada de una función en un punto es la pendiente de la recta tangente a la función en ese punto.

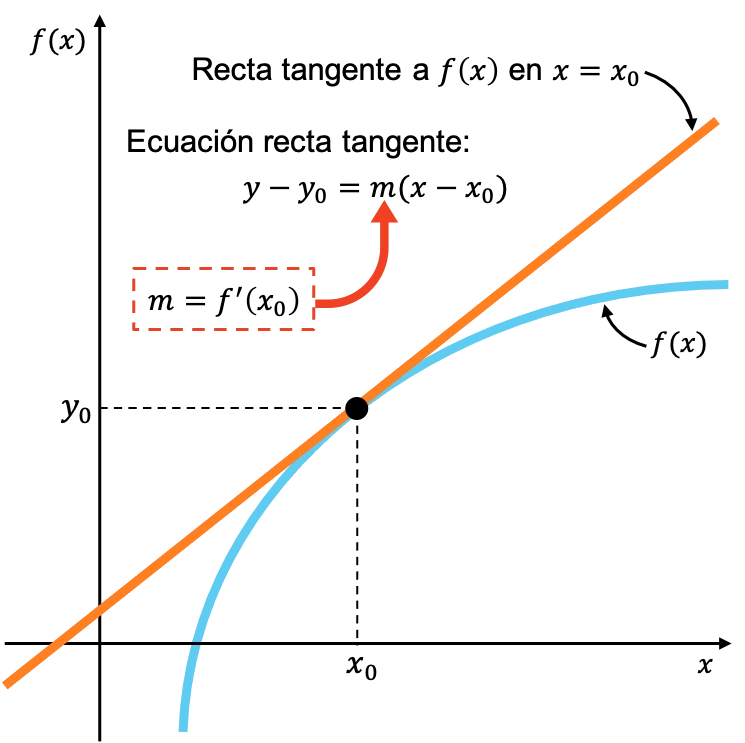
Si una función se puede derivar, se dice que la función es derivable.

La definición matemática de la derivada de una función es la siguiente:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Sin embargo, la derivada de una función no se suele calcular utilizando la fórmula anterior, sino que se aplican reglas de derivación según el tipo de función que sea. Más abajo veremos cuáles son las fórmulas de las derivadas y de las integrales.

➤ Ver: Tipos de derivadas

Integrales

Las integrales son las operaciones opuestas a las derivadas, de modo que las integrales son aquellas operaciones matemáticas mediante las cuales se puede calcular la función primitiva de una derivada.

Así pues, según el teorema fundamental del cálculo, al integrar una función continua y luego calcular su derivada se obtiene la función original.

Si una función tiene integral, se dice que esa función es integrable.

Asimismo, las integrales tienen su propia terminología:

$\displaystyle\int_a^b f(x)\ dx$

$\displaystyle\int$ es el signo de integración.
$\displaystyle a$ es el límite inferior de la integración.
$\displaystyle b$ es el límite superior de la integración.
$\displaystyle f(x)$ es la función a integrar, también llamada integrando.
$\displaystyle dx$ es el diferencial de x, que indica la variable de la función que se integra.

Además, existen dos tipos de integrales:

Integrales indefinidas: se resuelve la integral para todo el dominio de la función.

$\displaystyle\int f(x)\ dx$

Integrales definidas: se integra la función solo en intervalo marcado por los límites de integración.

$\displaystyle\int_a^b f(x)\ dx$

➤ Ver: Tipos de integrales

Tabla de derivadas e integrales

A continuación te dejamos la siguiente tabla en la que se resumen las fórmulas de las derivadas y las fórmulas de las integrales. Te resultará útil para resolver ejercicios en los que hay derivadas e integrales.

Tabla con las fórmulas de las derivadas y las integrales

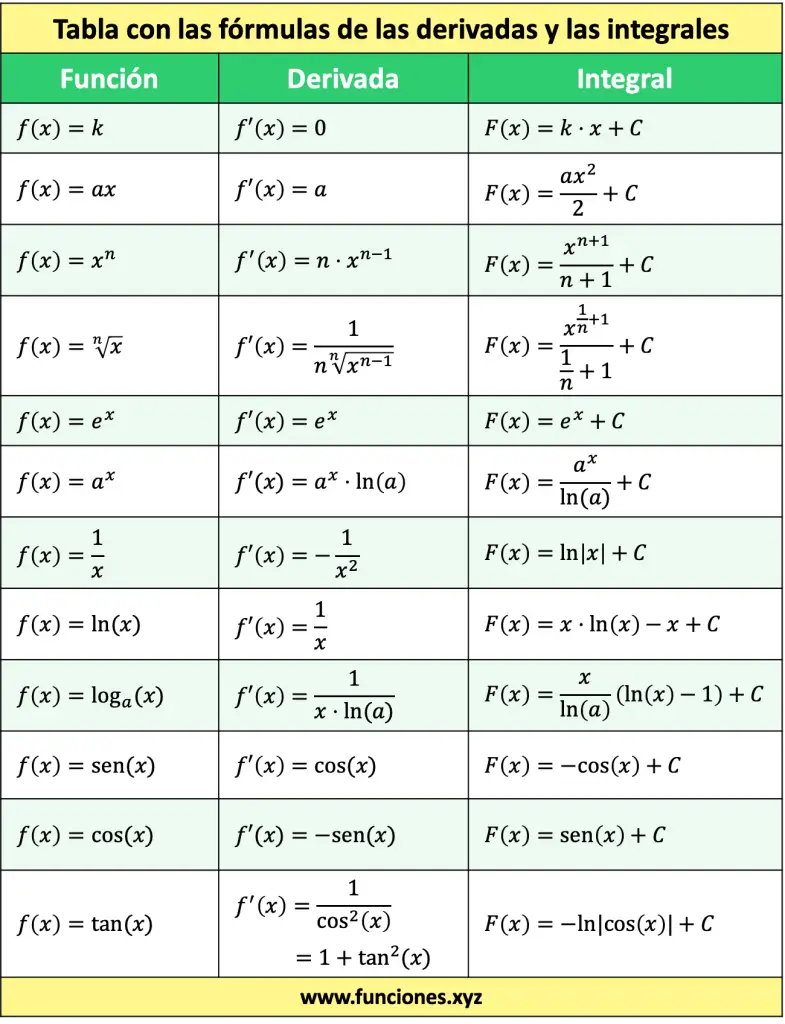
➤ Ver: Tabla de derivadas e integrales

Relación entre la derivada y la integral

El teorema fundamental del cálculo es un teorema que relaciona las derivadas con las integrales. En concreto, el teorema fundamental del cálculo indica que la derivación y la integración son operaciones inversas.

Por lo tanto, según el teorema fundamental del cálculo, al integrar una función continua y luego calcular su derivada se obtiene la función original.

En ocasiones, el teorema fundamental del cálculo se abrevia con las siglas TFC.

Además, partir del teorema fundamental del cálculo podemos calcular la derivada de una integral sin tener que resolver la integral. Puedes ver cómo se hace aquí:

➤ Ver: Fórmula del teorema fundamental del cálculo

Derivadas

Integrales

Tabla de derivadas e integrales

Relación entre la derivada y la integral

Deja un comentario Cancelar respuesta